Способы решения текстовых логических задач

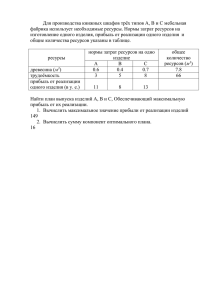
Способы решения
текстовых
логических задач
Выполнила: учитель
информатики МОУ-СОШ №21
Косенок Оксана Николаевна
А А  0
Закон исключения третьего А  А  1
Закон двойного отрицания А  А
Закон тождества
Законы идемпотентности
А  А  А, А  А  А
Законы коммутативности А  В  В  А, А  В  В  А
Законы ассоциативности А  В  С    А  В   С
А  В  С    А  В   С
Законы дистрибутивности
А  В  С    А  В    А  С 
А  В  С    А  В    А  С 
Законы де Моргана
А  В  А  В, А  В  А  В
Замена импликации
А  В  А В
Формальный
На вопрос: «Кто из трех учащихся изучал логику?» получен верный ответ: «Если изучал первый, то изучал и
второй, но неверно, что если изучал третий, то изучал и
второй». Кто из учащихся изучал логику?
Решение.
И1 – логику изучал первый,
И2 – логику изучал второй,
И3 – логику изучал второй.
Запишем формулы: И1  И 2  1, И 3  И 2  1.
И1  И 2  И 3  И 2  1
И1  И 2 И 3  И 2  И1  И 2 И 3  И 2 
 И1  И 3  И 2 И 2  И 3  И 2  И1  И 3  И 2  1
Ответ. Логику изучал третий ученик
Построение таблиц истинности
Три фирмы А, В и С, специализирующиеся на производстве и
продаже компьютеров, стремились получить максимальную
прибыль по итогам работы за год. Экономист, хорошо знавший
организацию работ в этих фирмах, высказал следующие
предположения:
1) фирма А может получить максимальную прибыль только
тогда, когда получат максимальную прибыль фирмы В и С;
2) либо фирмы А и С получат максимальную прибыль
одновременно, либо одновременно не получат;
3) для того, чтобы фирма С получила максимальную прибыль
за год, необходимо, чтобы и фирма В получила
максимальную прибыль.
По завершении года выяснилось, что экономист немного
ошибся: из трех утверждений истинными оказались только
два. Какие из названных фирм получили максимальную
прибыль?
Введем обозначения:
А – «фирма А получит максимальную прибыль за год»;
В – «фирма В получит максимальную прибыль за год»;
С – «фирма С получит максимальную прибыль за год»;
Составим таблицу истинности:
А В С
В С А  В  С  А С А С А С А  С  А  С
СВ
0
0
0
0
1
0
1
1
1
1
1
0
0
1
0
1
0
1
0
0
0
0
0
1
0
0
1
0
1
1
1
1
1
0
1
1
1
1
0
1
0
0
0
1
1
0
0
0
0
0
0
1
0
0
1
1
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
0
0
1
0
0
1
1
1
1
1
1
1
0
0
0
1
1
Ответ. Фирма А не получит максимальную прибыль, а фирмы В
и С получат.
Графический
Четыре марсианки, оказавшиеся на Земле, на
вопрос об их возрасте дали ответы:
1. И - 22 года, Е – 21 год.
2. О – 19 лет, И – 21 год.
3. А – 21 год, О – 18 лет.
Все марсианки разных возрастов, притом только
данных: 18, 19, 21 и 22. В каждом ответе одна часть
верна, другая – нет. Сколько лет каждой марсианке?
1. И - 22 года, Е – 21 год.
2. О – 19 лет, И – 21 год.
3. А – 21 год, О – 18 лет.
А21
О18 А21
О18
И21
О19
И22
А21
О18
О18
А21
О19
И21
Е21
Ответ. А - 21 год, О – 19 лет, И – 22 года, Е – 18 лет
Метод рассуждений
Разбирается дело Батончика, Ленчика и Пончика. Один из
них нашел и утаил клад. На следствии каждый из них сделал
два заявления:
1) Батончик: «Я не делал этого. Пончик делал это».
2) Ленчик: «Пончик не виновен. Батончик сделал это».
3) Пончик: «Я не делал этого. Ленчик не делал этого».
Суд установил, что один из них дважды солгал, другой
дважды сказал правду, третий один раз солгал, один раз
сказал правду. Кто из них утаил клад?
Утаил Батончик
Утаил Ленчик
Утаил Пончик
1) Батончик
0
0
1) Батончик
1
0
1) Батончик
1
1
2) Ленчик
1
1
2) Ленчик
1
0
2) Ленчик
0
0
3) Пончик
1
1
3) Пончик
1
0
3) Пончик
0
1
Ответ. Пончик утаил клад.
Список литературы
1. Информатика в школе. №6-2010. – М.: Образование и
Информатика, 2010.
2. Информатика в школе: Приложение к журналу
«Информатика и образование». №6-2005. – М.:
Образование и Информатика, 2005.