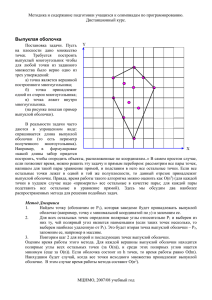
Целью данного курса является ознакомление с основными

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Математический факультет
Кафедра алгебры и топологии
РАБОЧАЯ
ПРОГРАММА
по дисциплине
«Вычислительные задачи геометрии»
для специальности: 511200 Математика. Прикладная математика
(магистратура)
очная форма обучения
Курс ……………………………..………….. 2
Семестр……………………………………... 4
Всего аудиторных часов…………………… 65
Лекции, час………………………………….. 34
Практические (семинарские) занятия, час… 17
Самостоятельная работа, час……………… 49
Зачет (семестр)……………………………… 4
Ижевск 2007
Рабочая программа составлена на основании __Государственного образовательного
(название документа, дата утверждения)
стандарта по специальности____________________________________________________
Составители рабочей программы
профессор, д.ф.-м.н.
(должность, ученое звание, степень)
______________
(подпись)
А.А.Грызлов
(Ф.И.О.)
Рабочая программа утверждена на заседании кафедры алгебры и топологии
«_____»______________ 2007 г.
Заведующий кафедрой
Декан факультета
______________
(подпись)
______________
(подпись)
А.А. Грызлов
(Ф.И.О.)
__А.С. Мерзляков
(Ф.И.О.)
Решение методической комиссии математического факультета
«____»_______________ 2007 г.
Председатель
методической комиссии
Согласовано с библиотекой УдГУ
Директор библиотеки УдГУ
Н.А. Баранова_____
(Ф.И.О.)
______________
(подпись)
_______________
_______________
(подпись)
2007 г.
________________
(Ф.И.О.)
2
1. Организационно-методический раздел
Целью данного курса является ознакомление с основными идеями,
понятиями и моделями относительно новой математической дисциплины,
непосредственно связанной с применением ЭВМ, вычислительной
геометрии. Основным содержанием дисциплины является исследования и
оценка сложности геометрических построений, анализ и построение
эффективности комбинаторных алгоритмов для решения геометрических
задач.
Данная дисциплина тесно связана с дисциплиной «Геометрическое
моделирование».
Вычислительная геометрия имеет широкий круг применений,
включающий распознавание образов, робототехника, машинная графика,
раскрой материалов и т. д.
Вычислительная геометрия опирается на много разделов как
классической, так и современной математики.
Результатом освоения курса является приобретение основ знаний в
области вычислительной геометрии, овладение основными методами
решения задач и их приложений.
Для освоения курса требуются знания следующих дисциплин:
аналитическая геометрия, дифференциальная геометрия, алгебра, теория
графов, теория алгоритмов, линейное программирование, анализ.
2. Объем и распределение часов по темам и видам занятий.
№ Наименование разделов и тем
Всего Лекций Лаборатор. Самостоят.
работа
Основные понятия, группы, 8
4
4
структуры.
Геометрический поиск
19
6
4
9
Выпуклые
оболочки. 19
6
4
9
Основные
алгоритмы,
приложения.
Близость.
Основные 18
6
3
9
алгоритмы,
варианты
и
обобщения.
Пересечения.
19
6
4
9
Геометрия прямоугольников.
17
6
2
9
100
34
17
49
3. Формы контроля знаний.
В конце семестра предусмотрен зачет.
3
4. Содержание курса.
Темы лекционных занятий и их краткое содержание.
1. Основные понятия, термины, структура. Методические истоки
дисциплины. Алгоритмические основы. Геометрические предпосылки.
Модели вычислений.
2. Геометрический поиск. Основные понятия. Задачи локализации
точки. Простые случаи. Локализация точки на планарном разбиении. Методы
полос, цепей, метод планарного сепаратора, метод трапеций.
Задачи регионального поиска. Метод многомерного двоичного дерева, метод
прямого доступа, метод дерева регионов.
3. Выпуклые оболочки. Основные алгоритмы. Алгоритм построения
выпуклой оболочки на плоскости. Выпуклые оболочки в пространствах
размерности больше двух. Выпуклая оболочка простого многоугольника.
Приложения к статистике.
4. Близость. Задачи, связанные с близостью. Задача о
единственности элементов. Решение задачи о ближайшей паре методом
«разделяй и властвуй». Решения задач о близости методом локусов;
диаграмма Вороного.
Евклидовы минимальные остовые деревья. Евклидова задача о
коммивояжере. Триангуляция с ограничениями.
5. Пересечения. Некоторые приложения: задачи удаления
невидимых линий и поверхностей, распознавание образов, трассировка и
размещение. Плоские приложения. Пересечение выпуклых многоугольников.
Пересечение звездных многоугольников. Пересечение отрезков. Пересечение
полуплоскостей и задачи линейного программирования. Трехмерные
приложения.
6. Геометрия прямоугольников. Некоторые приложения геометрии
прямоугольников; проектирование интегральных схем. Мера и периметр
объединения прямоугольников. Замыкание объединения прямоугольников.
Пересечение прямоугольников и связанные с этим задачи.
Вопросы к зачету.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Метод полос локализации точки.
Метод цепей локализации точки.
Метод планарного сепаратора.
Метод детализации триангуляции.
Метод трапеций.
Метод прямого доступа.
Метод дерева регионов.
Основные задачи построения выпуклой оболочки.
Алгоритм построения выпуклой оболочки на плоскости.
4
10.Обход методом Джарвиса.
11.Алгоритм типа «разделяй и властвуй».
12.Выпуклая оболочка простого многоугольника.
13.Приложение выпуклых оболочек к статистике.
14.Основные задачи, связанные с близостью.
15.Решение задачи о ближайшей паре методом локусов.
16.Диаграмма Вороного.
17.Евклидовы минимальные остовые деревья.
18.Евклидова задача о коммивояжере.
19.Пересечение выпуклых многоугольников.
20.Пересечение образов.
21.Пересечение полуплоскостей.
5. Учебно-методическое обеспечение курса.
1.
2.
3.
4.
1.
2.
3.
4.
Основная литература
Ф. Препарата, М. Шеймос. Вычислительная геометрия.
Введение. М.: Мир, 1989, 478 с.
Роджерс Д., Адамс Дж. Математические основы машинной
графики. М: Мир, 2001.
Кнут Д. Искусство программирования для ЭВМ. Т.3.
Сортировка и поиск. М.: Мир, 1978.
Горелик А.Л., Скрипкин В.А. Методы распознавания. М.:
Высшая школа, 1989.
Дополнительная литература
Ахо А., Хопкрофт Дж, Ульман Дж. Построения и анализ
вычислительных алгоритмов. М.: Мир, 1979.
Рейнгольз Э, Нивергельт Ю, Део Н. Комбинаторные алгоритмы:
теория и практика. М. Мир, 1980
Саати Т. Цельночисленные методы оптимизации и связанные
сними экстремальные проблемы. М.: Мир, 1973.
Рокефеллер А. Выпуклый анализ. М.: Мир, 1971.
5