Структурный анализ и синтез рычажных

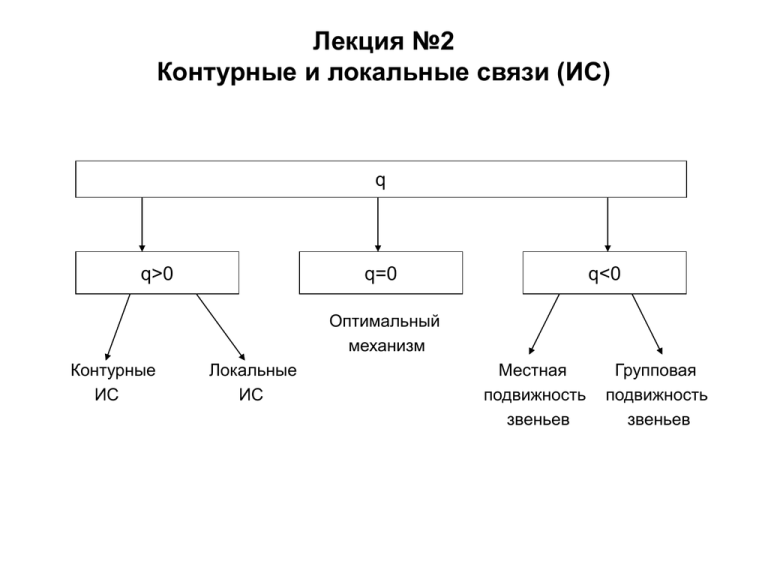
Лекция №2
Контурные и локальные связи (ИС)
q
q>0
q=0
q<0
Оптимальный
механизм
Контурные
ИС
Локальные
ИС
Местная
подвижность
звеньев
Групповая
подвижность
звеньев
Избыточные связи в механизмах
Механизмы с избыточными связями (q>1) нельзя собрать без деформации
звеньев. Такие механизмы требуют повышенной точности изготовления, в
противном случае в процессе сборки звенья деформируются, трение в
кинематических парах может сильно увеличиться и привести к заклиниванию
звеньев. Поэтому с этой точки зрения избыточные связи в механизме
нежелательны.
Однако в целом ряде случаев приходится сознательно проектировать и
изготавливать статически неопределимые механизмы с избыточными связями для
обеспечения нужной прочности и жесткости системы, особенно при передаче
больших сил.
Следует различать контурные избыточные связи, возникающие в замкнутых
кинематических цепях (контурах) механизма, и локальные избыточные связи в
кинематических парах.
Контурные избыточные связи
На рис. 1.4, а показан пятизвенный механизм двойного параллелограмма, выполненный по
плоской схеме. В этом случае WП  1
(одна обобщенная координата 1 ), n=4, p H  6 , p B  0 .
Следовательно, по формуле Чебышева
статически неопределимый,
q n  1  3 т.е.
4  2механизм
 6  1,
с одной избыточной связью.
Полученный после удаления звена 5 плоский четырехзвенный механизм с четырьмя
одноподвижными вращательными парами (W=1, n=3, p Н  4, рис. 1.4, б) является оптимальным:
q  1  3  3  2  4  0. Реальный механизм за счет неточностей изготовления (например,
вследствие непараллельности осей
и ) оказывается пространственным. По формуле
Малышева тогда в механизме оказываются три избыточные связи: q  W  6n  5p1  1  6  3  5  4  3.
Чтобы данный пространственный механизм был статически определимым, нужна его
другая структурная схема, полученная понижением класса некоторых кинематических пар,
например схема, изображенная на рис. 1.4, в, для которой q  W  6n  5p1  4p 2  3p 3  1  6  3  5  2  4  1  3  1  0.
Это механизм оптимальной структуры, но стоимость его изготовления повышается.
Дополнительная степень подвижности механизма
Возможен вариант механизма (рис. 1.4, г) с двумя сферическими парами ( p1  2 ,
p 3  2 ); в этом случае помимо основной подвижности механизма W0  1 появляется
местная подвижность WM  1 – возможность вращения шатуна 2 вокруг своей оси ВС.
Эта подвижность не влияет на основной закон движения механизма и может быть даже
полезна с точки зрения выравнивания износа шарниров В и С: при работе механизма
шатун 2 может самопроизвольно поворачиваться вокруг своей оси за счет переменных
W  W0  W
динамических нагрузок и вибраций. Следовательно,
и формула
Малышева
M 2
подтверждает, что такой механизм будет оптимальным:
q  2  6  3  5  2  3  2  0.
На рис. 1.4, д показан вариант схемы механизма, который имеет групповую
подвижность звеньев WГ  1 . Здесь две сферические пары установлены в шарнирах B и
D, и звенья 2 и 3 будут иметь дополнительную общую (групповую) подвижность в виде
возможного совместного вращения вокруг оси BD. Такой вариант механизма не
допустим, т.к. поведение выходного звена становится не предсказуемым.
Механизмы с незамкнутой кинематической цепью собираются без натягов, поэтому
они всегда оптимальны, без избыточных связей (q=0).
Итак, для реальных механизмов общее число степеней свободы определяется как
W  W0  Wм  WГ .
Локальные избыточные связи
Пояснения к рис. 1.5
Локальные избыточные связи возникают в сложных кинематических парах. На
рис. 1.5, а показан консольный вал 1, образующий со стойкой 2 вращательную пару
V класса. Прогиб вала в точке С под действием силы F может иметь недопустимо
большие значения.
Если вместо простой вращательной пары вал установить на двух опорах (рис.
1.5, б), то прогиб вала может быть уменьшен, но такая сложная кинематическая
пара дает 5 избыточных связей: W=1, n=1, p1  2 ; q  1  6  1  5  2  5.Число избыточных
локальных связей в кинематической паре, способствуя уменьшению податливости
конструкции, может оказаться вредным в случае изменения температурного
режима работы, при деформации стойки, при отклонениях размеров, формы и
расположения поверхностей элементов кинематической пары. Поэтому число
избыточных локальных связей приходится уменьшать. Так, если для вала правый
подшипник выполнить четырехподвижным линейным II класса (рис. 1.5, в), то число
связей будет уменьшено до двух, и прогиб вала в точке C (при а=в) уменьшится в 8
раз по сравнению с консольной установкой вала (рис. 1.5, а). Если оба подшипника
выполнить со сферическими элементами (рис. 1.5, г), причем левый подшипник
неподвижен в осевом направлении (фиксированная опора), а правый имеет осевую
подвижность (плавающая опора), то максимальный прогиб от нагрузки F в точке C
(при а=в) уменьшится только в два раза по сравнению с консольной опорой вала
только на левом конце (рис. 1.5, а), однако вал будет статически определимым:
q  1  6  1  2  1  3  1  0.
Структурный анализ плоских рычажных
механизмов
Структурный анализ состоит в представлении любого рычажного
механизма без избыточных связей (q=0) в виде совокупности первичного
(или основного) механизма и одной или нескольких структурных групп.
Первичный (или основной) механизм – это ведущее (начальное) звено,
которому приписывается обобщенная координата, и стойка. Число
первичных механизмов равно числу степеней свободы механизма.
Понятие
структурной
группы
введено
русским
ученым
Л.В. Ассуром в 1914 г. Структурная группа – это кинематическая цепь,
имеющая нулевую подвижность при соединении элементов ее концевых
кинематических пар со стойкой. Нулевая подвижность группы должна быть
потому, что требуемое число степеней свободы механизма W реализуется
только через движение начального звена (при W=1) или начальных
Wr  0 статически
звеньев (при W>1). Эти группы, имеющие
, называются
определимыми структурными группами.
Для плоской группы, содержащей лишь пары V класса (низшие пары),
уравнение Чебышева будет
WПГ  3n ПГ  2р НГ  0,
(2.1)
где WПГ – число степеней свободы плоской структурной группы; n ПГ и
p НГ – число звеньев и низших пар структурной группы Ассура. Отсюда
р НГ  3n ПГ / 2, а поскольку n ПГ и p НГ могут быть только целыми числами, то
их значения равны: n ПГ  2,4,6...; р НГ  3,6,9... .
Примеры структурных групп
Самая простая структурная группа ( n ПГ =2,p НГ =3) состоит из двух звеньев и трех пар.
Это группа II класса 2-го порядка или двухповодковая группа. Поводки – это звенья
группы, обладающие свободным элементом кинематической пары, служащим для
присоединения группы к механизму.
Т.к. кинематические пары V класса могут быть вращательными и поступательными,
двухповодковые группы имеют пять видов, различающихся числом и местом
размещения поступательных пар (рис. 2.1). Штриховой линией показана условная
стойка, обеспечивающая нулевую степень подвижности группы.
На рис. 2.2, а показана группа III класса 3 порядка или трехповодковая группа со
звеном 4, входящим в три кинематические пары; такое звено называют базисным. На
рис. 2.2, б показана группа IV класса 2 порядка. Обе группы имеют одни вращательные
пары, но они могут содержать одну или несколько поступательных пар и имеют
соответственно большее число видов.
а)
б)
Могут быть образованы группы и более высоких классов, но они редко применяются
в реальных механизмах.
Структурный синтез рычажных механизмов
Первый метод
Задача структурного синтеза механизмов является обратной по отношению к
задаче структурного анализа и состоит в проектировании структурной схемы
механизма. Синтез механизмов возможен двумя методами. Первый метод
заключается в присоединении к основному механизму одной или нескольких групп
Ассура. При этом следует иметь в виду, что добавление к механизму структурной
группы любого класса и вида не должно менять степени подвижности механизма.
На рис. 2.3 приведены примеры образования механизмов II класса (рис. 2.3, а) и III
класса (рис. 2.3, б).
Структурный синтез рычажных механизмов
Второй метод синтеза состоит в преобразовании одного из звеньев структурной
группы в два звена, образующих поступательную кинематическую пару V класса.
На рис. 2.4, а, б представлены структурные группы и гидрорычажные механизмы
соответственно II и IV классов, образованные этим методом.
Следует отметить, что для механизмов с гидроприводом заданным является
относительное движение поршня 2 в цилиндре 1, поэтому их структурный анализ
по Ассуру не возможен. Механизм должен рассматриваться как неделимая
структурная единица – гидрорычажный механизм соответствующего класса.