Паспорт открытого урока

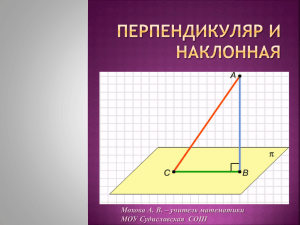
Паспорт открытого урока
Объект обучения: обучающиеся группы №13, I курс.
Предмет: Математика
Тема: Стереометрия. Перпендикулярность в пространстве.
Тема урока: «Перпендикуляр и наклонные»
Дата проведения: 20 октября 2009г.
Задачи:
 образовательные – ввести понятия: перпендикуляр, наклонная,
расстояние от точки до плоскости; повторить эти понятия из
планиметрии;
 развивающие – развитие навыков самостоятельной работы, умения
применять знания на практике; способствовать развитию
пространственного и логического мышления;
 воспитательные - создать условия для навыков коммуникативной
компетентности.
Тип урока: модульно - компетентностный.
Вид урока: урок усвоения новых знаний на основе имеющихся.
Межпредметные связи: техническая графика, физика.
Внутрипредметные связи: планиметрия.
Методы обучения: репродуктивный (самостоятельная работа, беседа,
выполнение упражнений, обсуждение).
Средства обучения:
 учебно-раздаточный
материал;
 листы с заданиями;
 дневник урока;
 учебная доска;
 компьютер с проектором;
 стенд «К теме» с рисунками
и терминами.
Форма обучения: коллективная, индивидуальная.
Форма учебного занятия: классно-урочная.
Структура учебного занятия
1). Организационно-мотивационный этап:
(5 минут)
1.1. Постановка целей и мотивация изучения темы.
1.2. Предварительное определение уровня знаний учащихся.
(Задание №1)
2). Организация самостоятельной работы учащихся по вопросам темы
урока:
2.1. Перпендикуляр и наклонная.
(15 минут)
(Задание №№ 2, 3)
2.2. Расстояния между точкой, прямыми и плоскостями. (15 минут)
(Задание №4)
3). Подведение итогов урока:
(10 минут)
3.1. Проверка степени усвоения материала:
а) через м/м проектор проверяем правильность выполнения
заданий 2, 3,4;
б) систематизация знаний, полученных на уроке через устный
опрос.
3.2. Домашнее задание.
1) повторить теорему Пифагора;
2) выполнить задание №5
3.3. Оценка средств обучения и деятельности педагога.
(дневник урока)
ПРИЛОЖЕНИЕ (презентация)
Лист с заданиями №1
1.2 Предварительное определение уровня знаний
учащихся.
Задание №1: Попытайтесь ответить на вопросы:
1. Угол между двумя прямыми равен 90о. Как называются такие прямые?
2. Прямые а и т взаимно перпендикулярны, прямая в перпендикулярна а.
чему равен угол между прямыми в и т?
3. Одна из двух данных прямых перпендикулярна плоскости, а вторая не
пересекает эту плоскость. Могут ли быть параллельными эти прямые?
4. Одна из скрещивающихся прямых перпендикулярна плоскости.
Перпендикулярна ли этой плоскости вторая прямая?
2.1. Перпендикуляр и наклонная
1. Перпендикуляр и наклонная на плоскости.
Пусть на плоскости дана прямая а и
точка А, которая не принадлежит этой
прямой.
АВ – перпендикуляр, опущенный из
точки А на прямую а.
Отрезок АС, соединяющий точку А с
произвольной точкой С на прямой а,
C
называется наклонной, проведенной из
точки А на прямую а.
Точка С называется основанием наклонной.
Отрезок ВС называется проекцией наклонной на прямую а.
АВ ⊥ а; В – основание перпендикуляра; АВ – перпендикуляр; АС –
наклонна; С – основание наклонной; ВС – проекция наклонной.
Любая наклонная, проведенная из точки А к прямой а, больше
перпендикуляра, опущенного из этой же точки: АС > АВ.
∙
2. Перпендикуляр и наклонная в пространстве.
Пусть 𝜶 – данная плоскость, А – данная точка,
l
А ∉ 𝜶. Проведем через точку А прямую l ⊥ 𝜶.
Обозначим В – точку пересечения прямой l с
плоскостью 𝜶.
Отрезок АВ называется перпендикуляром,
опущенным из данной точки на данную плоскость.
Точка В называется основанием
перпендикуляра.
Из данной точки, не лежащей на данной
плоскости, можно провести перпендикуляр к данной плоскости, и только один.
Наклонной из данной точки А к плоскости 𝜶 называется любой отрезок,
отличный от перпендикуляра АВ, соединяющий точку А с произвольной точкой
С плоскости 𝜶.
Точка С называется основанием наклонной.
Отрезок ВС называется проекцией наклонной АС на плоскость 𝜶.
АВ ⊥ 𝜶; В – основание перпендикуляра; АВ – перпендикуляр; АС –
наклонна; С – основание наклонной; ВС – проекция наклонной на плоскость 𝜶.
Любая наклонная, проведенная из точки А к плоскости 𝜶, больше
перпендикуляра, опущенного из этой же точки: АС > АВ.
Лист с заданиями №2
Задание №2: Скопируйте рисунок в тетрадь и подпишите указанные
элементы.
∙
∙
∙
Задание №3: Внимательно изучите рисунок. В следующих утверждениях
заполните пропуски подходящим по смыслу словами: «больше», «меньше» или
«равно» и запишите эти выводы в тетрадь.
а) Равные наклонные имеют ……………………………. проекции.
б) Большей проекции соответствует
………………………………… наклонная.
∙
в) Меньшей наклонной соответствует
…………………………………. проекция.
г) Перпендикуляр ……………………………
наклонной.
д) Равные проекции имеют
………………………………… наклонные.
∙
∙
∙
∙
2.2. Расстояния между точками, прямыми и плоскостями.
Задание №4: Внимательно изучите рисунки таблицы приведенной выше и
заполните подходящими по смыслу пропуски в столбце «Понятие расстояния».
№
п/п
1
Чертеж
Понятие расстояния
∙
А
∙В
2
а
Расстояние между параллельными
прямыми – это длина их общего
……………………………., т.е, расстояние от
произвольной ……………….. одной из
параллельных ………………….. до другой.
C
∙
b
Расстояние от точки до прямой, не
содержащей эту точку, есть длина
………………………………, проведённого
из этой точки на ………………………. .
А
∙
3
Расстояние между двумя точками А и В –
это длина ……………….. АВ.
т
В
4
A
𝜶
5
∙
∙B
∙
a
𝜶
Расстояние от точки до плоскости, не
содержащей эту точку, есть длина
……………………………….., опущенного
из этой точки на ………………………… .
A
∙B
Расстояние между прямой и параллельной
ей плоскостью – это ………………………
от произвольной точки ………………… до
плоскости.
6
𝜶
𝜷
7
∙A
∙B
Расстояние между параллельными
плоскостями - это расстояние от
произвольной ……………………. одной из
этих ………………………………. до другой
………………………......... .
Общим перпендикуляром двух
скрещивающихся прямых называется
………………………. с концами на этих
прямых, являющийся …………………..
………………… к каждой из них.
Расстоянием между скрещивающимися
прямыми называется длина их общего
………………………………… . Оно равно
расстоянию между …………………………..
плоскостями, проходящими через эти
……………………………………………… .
3.1. Проверка степени усвоения материала:
Ответьте на вопросы:
1. Что такое перпендикуляр, опущенный из данной точки на плоскость?
2. Что называется основанием перпендикуляра, проведенного к плоскости?
3. Что такое наклонная, проведенная из данной точки к плоскости?
4. Что называется основанием наклонной, проведенной к плоскости?
5. Что такое проекция наклонной на плоскости?
3.2. Домашнее задание.
1) повторить теорему Пифагора;
2) выполнить задание №4
Задание №4: Рассмотрите рисунок и ответьте на вопросы (устно):
а) Чем является отрезок АС?
б) Чем является отрезок АВ?
в) Чем является отрезок ВС?
г) Как называется полученная фигура АВС?
д) Как называются стороны АB и ВС у этой
фигуры?
е) Как называется сторона AC этой фигуры?
ж) Какую теорему применяют при нахождении неизвестных сторон этой
фигуры?