Аналитическая геометрия на плоскости

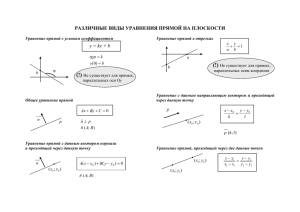
Аналитическая
геометрия
на плоскости
Определение: Линией на плоскости
называется множество точек, обладающих
некоторыми свойствами.
Определение: Уравнением линии
(кривой) на плоскости ОХУ называется
уравнение, которому удовлетворяют
координаты Х и У каждой точки данной
линии и не удовлетворяют координаты
точки, не лежащий на этой линии.
Определение: т.М(х; у) передвигается по
линии, х и у меняются, удовлетворяя
уравнению линии, поэтому координаты
т.М называется текущими координатами
точки линии.
Определение: Линия называется линией или
кривой n-ого порядка, если она определяется
уравнением n-ой степени относительно
текущих прямоугольных координат
Общее уравнение прямой.
A( x  x0 )  B( y  y0 )  0
Ax  By  C  0
.
;
Каноническое уравнение прямой.
x  x0 y  y 0

m
n
Уравнение прямой « в отрезках»
x
y

1
a
b
Параметрические уравнения прямой.
x  x0 y  y 0

=t
m
n
 x  x0  mt

 y  y 0  nt
t Є (-∞; + ∞)
Уравнение прямой,
проходящие через две заданные точки.
x  x1
y  y1

x 2  x1
y 2  y1
Уравнение прямой с угловым коэффициентом:
Y  Kx  b
Угол между двумя прямыми:
tg μ =
k 2  k1
1  k1 k 2
Условия параллельности и
перпендикулярности.
А)
L1 || L2
,
L1  L2 ,
K1  K 2
K1 * K2  1
В)
L1 || L2
;
n1 ||
A1
B1

A2
B2
n2
Г)
L 1 L2; n1
 n2
A1 A2  B1B2  0
Точка пересечения двух прямых
L1: A1x + B1y + D1 =0 ,
L2: A2x + B2y + D2 =0,
L1 Ω L2 = M(x0; y0)
A2x0 + B2y0 + D2= 0
A1x0 + B1y0 + D1=0
(x0; y0) есть решение системы
Взаимное расположения двух
прямых.
Если прямые пересекаются, то
система имеет единственное решение
Если прямые параллельны, то
система не имеет решения;
Если прямые совпадают, то
система имеет бесконечно много
решений.
Уравнение прямой, проходящей
через данную точку в данном
направлении:
у – у0= к (х – х0)
Уравнение пучка прямых.
Если k дано, то уравнение
y  y0  k ( x  x0 )
определяет одну прямую, если
k – меняется,
то уравнение y  y0  k ( x  x0 )
определяет пучок прямых, проходящих
через точку M1 ( x1; y1 ) .
,
Расстояние от точки до прямой:
L: Ах + В у + D =0; M1 ( x1; y1 )
d
Ax1  By1  D
A B
2
2
n 
A B
2
2
Кривые II порядка.
Определение:
Кривая называется кривой второго
порядка, если она определена
уравнением
Ax  Bxy  Cy  Dx  Ey  F  0
2
2
Определение:
Кривая второго порядка
Ax  Bxy  Cy  Dx  Ey  F  0
2
2
называется эллипсом ,
если коэффициенты А и С с одинаковыми
знаками, т.е. А·С>0.
A( x  x0 )  C ( y  y0 )  0
2
2
1)
Пусть А и С, иначе ·( -1).
Δ>0, 
действительный эллипс
при х0= у0=0
2
2
x
y


1
2
2
a
b
a

;b 
A

B
Каноническое уравнение эллипса; полуоси эллипса.
Частный случай а = в, ( А=С)
получаем окружность
( х – х0) 2 + ( у – у0)2=r2
2)
Δ= 0, то выраженный эллипс, т.е. О (0;0) .
3)
Δ<0, кривая не имеет действительных
точек, мнимым фокусом.
Определение:
Кривая второго порядка
y  y0  k ( x  x0 )
называется кривой гиперболического
типа, если А· С<0 (разные знаки)
Пусть А>0 С<0.
1)Δ>0, гипербола с каноническим уравнением
2
2
x
y
 2 1
2
a
b
a
b

A

C
- действительная полуось
- мнимая полуось
2) Δ<0, гипербола,
сопряженная к гиперболе
3)Δ=0, пара пересекающихся
прямых, вырожденная гипербола.
Определение:
Кривая второго порядка называется нецентральной,
если она или не имеет центра симметрии, или же
имеет бесконечно много центров симметрии.
Определение:
Кривая
( y  y0 )  2 p ( x  x 0 )
2
называется параболой.
О΄ ( x0 ; y0 )- вершина параболы, р–
параметр параболы.