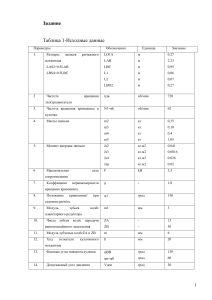
Силовой анализ рычажных механизмов
реклама

Лекция №5 Силовой анализ рычажных механизмов Во время движения механизма в его кинематических парах действуют силы, являющиеся силами взаимодействия между звеньями. Эти силы относятся к категории внутренних сил по отношению к механизму в целом. Знание сил в кинематических парах в дальнейшем позволит решить следующие инженерные задачи: расчет звеньев механизма на прочность, жесткость, износоустойчивость и т.п.; расчет подвижных соединений звеньев на долговечность; выбор мощности двигателя и т.д. Задачей силового анализа рычажных механизмов является определение: 1) сил и пар сил, приложенных к механизму извне; 2) внутренних сил, действующих в кинематических парах; 3) уравновешивающей силы или уравновешивающего момента, которые надо приложить к начальному звену для обеспечения требуемого закона движения выходного звена. Если начальное звено совершает поступательное движение, то определяют одну уравновешивающую силу Fy , при вращательном движении начального звена определяют уравновешивающий момент M y . Для силового анализа рычажных механизмов используют метод кинетостатики, условно приложив к каждому подвижному звену механизма главный вектор и главный момент сил инерции. Тогда под действием внешних сил и моментов и инерционных сил весь механизм будет находиться в равновесии. Для кинетостатической определимости плоский механизм не должен иметь избыточных связей. Условия кинетостатической определимости плоских рычажных механизмов Сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности. Во вращательной паре сила, действующая на звено i со стороны звена j Fij направлена нормально к цилиндрической поверхности соприкосновения обоих звеньев, т.е. проходит через центр шарнира А (рис. 2.11, а). Модуль силы Fij и угол неизвестны. Эта пара приносит в расчет две неизвестные величины. В поступательной паре сила направлена по нормали к поверхности соприкосновения звеньев (рис. 2.11, б). Модуль силы и плечо неизвестны. И эта низшая пара приносит в расчет две неизвестные величины. В поступательной паре сила Fij направлена по нормали n-n к поверхности соприкосновения звеньев (рис. 2.11, б). Модуль силы и плечо h неизвестны. И эта низшая пара приносит в расчет две неизвестные Fij величины. Если плоская кинематическая цепь содержит n подвижных звеньев и pнизших кинематических пар, то H для нее суммарное количество неизвестных величин в кинематических парах равно 2p H , а количество уравнений равновесия равно 3n, т.к. для каждого звена можно составить 3 уравнения кинетостатики: Fx 0, Fy 0, M 0 0. Для кинетостатической определимости такой цепи необходимо выполнение условия 3n 2p H или 3n 2p H 0 . Сопоставив это выражение с выражением, полученным для плоской структурной группы любого класса с низшими парами, можно сделать вывод, что любая структурная группа, сколь бы сложной она ни была, является статически определимой. Mетодика силового анализа рычажных механизмов без избыточных связей такова: силовой анализ ведется погруппно, начиная от группы, наиболее удаленной от первичного механизма, и заканчивая расчетом самого первичного механизма. Таким образом, силовой расчет проводится в порядке, обратном кинематическому. При наличии избыточных связей в механизме (q nметод 0) кинетостатики не пригоден, необходимо использовать методы теории упругости. Исходные данные для силового анализа 1) кинематическая схема; 2) массы и моменты инерции звеньев, положения центров масс звеньев; 3) закон движения механизма; 4) внешнее силовое нагружение. Внешнее силовое нагружение может быть представлено следующей группой сил и моментов. 1. Массовые внешние силы: силы тяжести G i m i g ; силы инерции внешние, связанные с движением объекта, на котором находится механизм, FПГi mi gП Г , FПВi mi gП B , где m i - масса i-того звена, g – а а ПГ ПВ ускорение свободного падения, и - горизонтальная и вертикальная перегрузки: ПГ Г ; ПВ В . g g Работа этих сил за цикл равна нулю. 2. Массовые внутренние силы – это главный вектор сил инерции и главный момент сил инерции звена F ui mi a Si , M ui J Si i ; где a Si - линейное ускорение центра масс звена, i - угловое ускорение звена, J Si - момент инерции i - того звена относительно оси, проходящей через центр масс звена перпендикулярно плоскости его движения. Работа этих сил за цикл также равна нулю. 3. Силы полезного сопротивления – это силы, для преодоления которых предназначен механизм. Ими могут быть силы резания, давления, сжатия и другие технологические силовые факторы. Работа за цикл этих сил – отрицательная величина. 4. Силы вредного сопротивления – это внешние и внутренние силы трения. Внешние силы трения возникают в исполнительном устройстве, приводимом в действие механизмом. Внутренние силы трения возникают в кинематических парах. Работа за цикл этих сил также отрицательна. 5. Движущие силы и моменты – это уравновешивающая сила Fy или уравновешивающий момент M y , которые должны быть приложены к начальному звену со стороны двигателя. Эти силы за цикл совершают положительную работу. Аналитический метод силового анализа кривошипноползунного механизма Исходными данными являются: 1) кинематическая схема; 2) массы звеньев 2 и 3; причем, центр масс звена 3 располагается в точке В, т.е. x S3 x B , y S3 y B 0 т.к. механизм центральный; масса звена 1, как правило, пренебрежимо мала; 3) момент инерции звена 2; 4) величина горизонтальной перегрузки; 5) постоянная сила трения в уплотнениях при движении поршня 3 FT 3 ; 6) сила сопротивления FC3 (1 ) , действующая на поршень, заданная в табличной форме. Схема нагружения структурной группы и начального звена Алгоритм силового анализа кривошипно-ползунного механизма Силовой анализ следует начать со структурной группы, состоящей из звеньев 2 и 3. Неизвестные силы во вращательных кинематических парах разложим на составляющие по осям координат x и y. Неизвестными являются силы F21x , F21y , сила F34 и ее плечо h 34 , а также модуль и направление сил взаимодействия в шарнире В, связанных соотношением F23 F32 . Для определения шести неизвестных необходимо составить шесть уравнений равновесия. 1. Здесь и дальше можно не рассматривать уравнение равновесия, а писать только 2,3 Fx 0 . Следовательно, F21x FПГ2 Fu 2 x FПГ3 (FC3 FT 3 ) Fu 3 0. (2.63) 2. M B 0. ИлиF21x ( y B y A ) F21y ( x B x A ) G 2 ( x B x S2 ) FПГ 2 ( y B yS2 ) (2.64) 2 Fu 2 x ( y B yS2 ) Fu 2 y ( x B x S2 ) M u 2 0 F21y Fy 0 F21y G2 3. Fu 2 y G3 F34 Следовательно, 0 F34 2,3 4. 5. 6. M B 0 Так как все силы, приложенные к звену 3, проходят через точку В, то и сила F34 3 проходитhчерез 34 0. точку В, т.е. плечо Сумма проекций всех сил, приложенных к звену 3, на ось х равна нулю FX 0: FC 3 FT 3 FПГ 3 Fu3 F32 X 0 F32 x Fy 0 : G3 F34 F32y 0 F32y 3 также (2.66) (2.67) 3 Модуль силы во вращательной кинематической паре, например А, определяется формулой F21 F212 X F212 y , а направление силы определяется углом (рис. 2.11, а) F21y arctg F , приF21X 0. 21X acrtg F21y , приF 0. 21X F21X (2.68) (2.69) Для определения силы F14 в кинематической паре О и уравновешивающего момента M y необходимо рассмотреть равновесие начального звена (рис. 2.12, б). Величина уравновешивающего момента определяется из уравнения равновесия звена 1 M O 0 Или F12X y A F12y x A M y 0 (2.70) 1 Очевидно, что F14X F12X , F14y F12y . Силовые характеристики кривошипно-ползунного механизма Аналитический метод силового анализа механизма с гидроцилиндром. Постановка задачи. Известны кинематическая схема (рис. 2.10, а); массы и моменты инерции звеньев; величина горизонтальной перегрузки П Г ; постоянная величина момента трения в шарнире С М Т 3 ; сила сопротивления FC3 , действующая на звено 3 в точке S3 , заданная в табличной форме; постоянная сила трения в гидроцилиндре FT 21 . Необходимо определить силы во вращательных кинематических парах А, В и С, силу в поступательной кинематической паре, образованной цилиндром 1 и поршнем со штоком 2, а также уравновешивающую силу Fy , которую надо приложить со стороны жидкости к поршню цилиндра, чтобы весь механизм находился в равновесии. Поскольку механизм с гидроцилиндром является неделимой структурной единицей, силовой анализ проводится для всего механизма. Расчет состоит из двух этапов. На первом этапе расчета определяют силы в шарнирах А, В и С, мысленно “замораживая” поршень со штоком в гидроцилиндре в расчетном положении. Таким образом, механизм рассматривается как двухповодковая группа первого вида. На втором этапе, отделив звено 1 от звена 2, определяют остальные неизвестные силы. Схема механизма с “замороженным” гидроцилиндром со всеми действующими на него силами и моментами представлена на рис. 2.14, а. На рисунке не показаны силы инерции и моменты инерции звеньев, которыми можно пренебречь ввиду их малости. Силовое нагружение механизма с гидроцилиндром FПГ3 S3 FC a) а) 3 MT3 G 3 y F34 F34x П y F14y FПГ A F14x 1 FПГ2 1 F3 Sц FПГi FПВi В F23x F23y FT12 FT21 F23 G2 1 F21 Fy 2 x А F21 V21 В Sn K φ1 ПГ Sn G б) Si 3 2 2 V21 В x C Fy FПГ2 K F23y G2 F23x Рис. 2.14 F23 Алгоритм силового анализа механизма с гидроцилиндром Шесть уравнений равновесия, из которых можно определить неизвестные силы, действующие во вращательных парах А, В и С. 1). M B 0 Или 1, 2 (2.71) M B (F14X ) M B (F14y ) M B (G1 ) M B (FПГ1 ) M B (G 2 ) M B (FПГ2 ) 0; 2). M C 0 Или 1, 2 , 3 (2.72) M C (F14X ) M C (F14y ) M C (G1 ) M C (FПГ1 ) M C (G 2 ) M C (FПГ 2 ) M C (G 3 ) M C (FПГ3 ) M C (FC3 ) M T 3 0; Совместное решение уравнений даст значения неизвестных сил F14X и F14y . 3). FX 0 Или F14 X FПГ1 FПГ 2 F34 X FПГ3 FC3 0 F34 x 1, 2 , 3 4). Fy 0 Или F14y G1 G 2 F34y G3 0 F34y (2.73) 5). FX 0 Или F14 X FПГ1 FПГ 2 F23X 0 F23 x (2.75) 6). Fy 0 Или F14y G1 G 2 F23y 0 F23y (2.76) (2.74) 1, 2, 3 1, 2 1, 2 Для определения уравновешивающей силы F y и силы, действующей в поступательной паре звеньев 1 и 2, отделим поршень со штоком от цилиндра и рассмотрим равновесие начального звена 2 (рис. 2.14, б). Поступательная пара образована двумя точками контакта цилиндра и поршня со штоком K и K , в которых действуют силы F21 и F21 . Для определения трех неизвестных сил можно составить три уравнения равновесия 1). M k 0 Или 2 (2.77) ) M k (F23X ) M k (F23y ) 0 M k (G 2 ) M k (FПГ2 ) M k (F21 2). M k 0 Или ) M k (F23X ) M k (F23y ) 0 M k2(G 2 ) M k (FПГ2 ) M k (F21 (2.78) 3) Сумма всех сил, действующих на звено 2, в проекции на линию АВ равна нулю FAB 0 Или 2 Fy FПГ2 cos 1 G 2 sin 1 F23X cos 1 F23y sin 1 0 (2.79) , F21 , Fy Из трех уравнений определяются соответственно силы . F21 Силовые характеристики механизма с гидроцилиндром V21›0 V21‹0