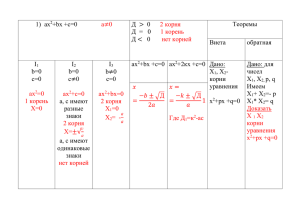
Квадратные уравнения
реклама

Квадратные уравнения Чтобы решить уравнение, Корни его отыскать, Нужно немного терпения, Ручку, перо и тетрадь. Минус напишем сначала, Рядом с ним пополам, Плюс - минус знак радикала, С детства знакомого нам. Работу выполнила: Кристина Кальде, 8А Содержание Определение Классификация Способы решения Биквадратное уравнение Биография Виета Определение Квадратным уравнением называется уравнение ax2+bx+c=0, где a, b, с–заданные числа, x-неизвестное. Числа a, b, c носят следующие названия: a - первый коэффициент, b - второй коэффициент, с - свободный член. Выражение b2-4ac называется дискриминантом квадратного уравнения. Классификация ∙Полные (ax2+bx+c=0, где коэффициенты b и с отличны от нуля ) ∙Неполные (ax2+bx+c=0, где хотя бы один из коэффициентов b или c равен нулю ) ∙Приведённые (x2+bx+c=0, т.е. уравнение, старший коэффициент которого равен единице ) Способы решения полных квадратных уравнений X= -b±√b2-4ac 2a ∙ D=b2-4ac X= -b±√D 2a Способы решения неполных квадратных уравнений ax2=0 x2=0 х1,2=0 ax2+bx=0 x(ax+b)=0 x1=0 ax+b=0 ax=-b x2=-b/a ax2+c=0 ax2=-c x2=-c/a Способы решения приведённых квадратных уравнений По формулам Виета. Если x1 и x2 -корни уравнения 2 x +px+q=0, то справедливы формулы: x1+x2=-p x1*x2=q т.е. сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену По формуле корней Биквадратное уравнение Определение Уравнение ax4+bx2+c=0 называют биквадратным. Пример: 9x4+5x2-4=0 Обозначим x2=t. Тогда данное уравнение примет вид 9t2+5t-4=0 Откуда t1=4/9, t2=-1. Уравнение x2=4/9 имеет корни x1=2/3 и x2=-2/3, а уравнение x2=-1 не имеет действительных корней. Биография Виета Франсуа Виет родился в 1540 году в городе Фонтене ле-Конт провинции Пуату. Получив юридическое образование, он в 19 лет успешно занимался адвокатской практикой в родном городе. Как адвокат Виет пользовался у населения авторитетом и уважением. Он был широко образованным человеком. В 1571 году Виет переехал в Париж и там познакомился с математиком Пьером Рамусом. Благодаря своему таланту и, отчасти, благодаря браку своей бывшей ученицы с принцем де Роганом, Виет сделал блестящую карьеру и стал советником Генриха III, а после его смерти - Генриха IV. В последние годы жизни Виет занимал важные посты при дворе короля Франции. Умер он в Париже в самом начале семнадцатого столетия. Есть подозрения, что он был убит.