Л2 Поверхности, виды, аксонометрические проекции
реклама
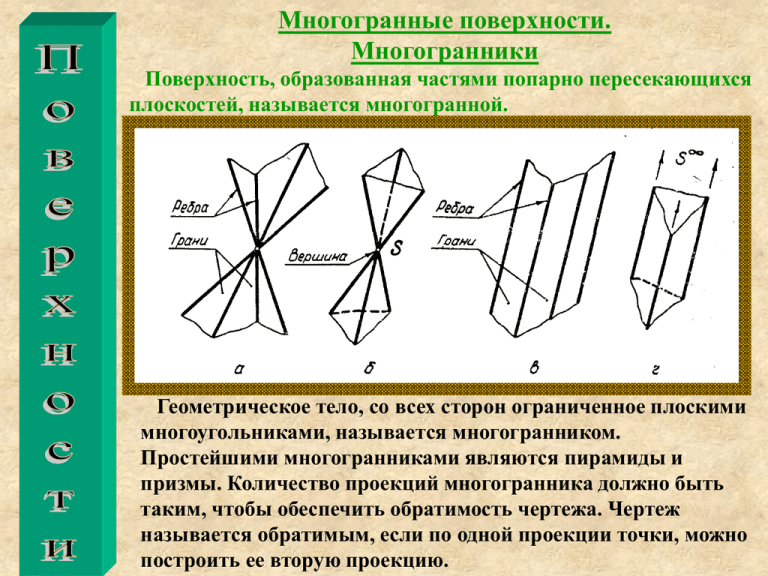
Многогранные поверхности. Многогранники Поверхность, образованная частями попарно пересекающихся плоскостей, называется многогранной. Геометрическое тело, со всех сторон ограниченное плоскими многоугольниками, называется многогранником. Простейшими многогранниками являются пирамиды и призмы. Количество проекций многогранника должно быть таким, чтобы обеспечить обратимость чертежа. Чертеж называется обратимым, если по одной проекции точки, можно построить ее вторую проекцию. Многогранные поверхности. Многогранники Видимость проекций линий, расположенных внутри очерка, определяется при помощи конкурирующих точек. Кривые поверхности Кривые поверхности как объекты исследования или применения при создании различных технических форм могут быть заданы различно. В инженерной практике поверхность, как правило, задается чертежом, иногда уравнением. Для того, чтобы построить чертеж поверхности, необходимо предварительно выявить ее определитель. Определителем поверхности называют совокупность всех условий, однозначно задающих поверхность. Определитель состоит из 2х частей: 1. Геометрической части 2. Алгоритма. Примеры выявления определителя Через три точки А,В,С не принадлежащие одной прямой, можно провести одну и только одну плоскость. Точки А,В,С составляют геометрическую часть определителя плоскости. Вторая часть определителя, т.е. алгоритм построения в плоскости любых линий и точек выражается рассмотренными ранее условиями принадлежности прямой и точки плоскости. На чертеже плоскость задана проекциями геометрической части своего определителя. Примеры определителей для простейших поверхностей. 1) - цилиндрическая поверхность вращения. 2) - коническая поверхность вращения. 3) - сфера (геометрическая часть определителя сферы состоит из точки О-центра сферы и точки М, принадлежащей ее поверхности. Алгоритм построения любой точки сферы заключается в проведении через точку О произвольной прямой и откладыванием на нем отрезка, который равен радиусу. Очерк поверхности При чтении чертежа немаловажную роль играет его наглядность. Для придания чертежу поверхности большей наглядности прибегают к построению очерков ее проекций или проекций достаточно плотного каркаса ее образующих (в случаях, когда проекции поверхности не имеют определенного очерка) на основании алгоритмической части ее определителя. Очерк проекции поверхности является проекцией соответствующей линии видимого контур Линия видимого контура поверхности разделяет ее на части- видимую, обращенную к наблюдателю, и невидимую. На рисунках конус вращения и сфера заданы проекциями геометрической части своего определителя, а на чертежах для тех же поверхностей построены очерки их проекций. Последние, безусловно, обладают большей наглядностью и выразительностью. Наибольшее применение в технике получили следующие классы кривых поверхностей: 1) поверхности вращения, в частности поверхности вращения второго порядка; 2) линейчатые поверхности: развертывающиеся; неразвертывающиеся; винтовые. Поверхности вращения При проектировании различных инженерных сооружений, машин и механизмов наибольшее распространение получили поверхности, образующиеся вращением прямой линии и кривых второго порядка. а)- цилиндр вращения б) конус вращения в)- однополостный гиперболоид вращения Тор Тор- поверхность 4го порядка Сфера Видом называется изображение обращенной к наблюдателю видимой части поверхности предмета Виды-основные дополнительные местные Основными называют виды, полученные проецированием предмета на шесть основных плоскостей проекций . Размещение основных видов Основные виды, расположенные в проекционной связи не надписываются Построение изометрической проекции окружности