Лекция 14 • Химические равновесия (продолжение). при протекании нескольких химических реакций

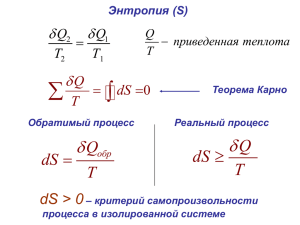
Лекция 14
• Химические равновесия (продолжение).
• Расчет равновесного состава и выходов продуктов
при протекании нескольких химических реакций
(на примере реакции образования NH3,
гидрирования этилена).
• Третий закон термодинамики. Формулировка
Нернста и формулировка Планка.
•Таблицы т/д величин
•Адсорбция
Лекция 13
Уравнения Гиббса-Дюгема-Маргулеса.
Обобщенное уравнение Гиббса-Дюгема.
Мольные (интегральные) и парциальные мольные
величины. Их определение для бинарных
растворов.
Зависимость парциальных мольных объемов от
состава в системе Н2О - С2Н5ОН
Химические равновесия в растворах. Константы
равновесия при различном выборе стандартных
состояний для участников реакции. Химическое
равновесие в разбавленном растворе. Влияние
инертного растворителя.
Отрицательный парциальный мольный объем
1 моль MgSO4
T,p = const
nH 2 O ; nMgSO4
nH 2 O ; nMgSO4
nH 2 O
nH 2 O
 V

 nMgSO4
nMgSO4
nMgSO4

V (nMgSO4  1, nH 2 O ) V (nMgSO4 , nH 2 O )

 0;

1
T , p ,nH 2O
nH
2O
nMgSO
4
1
ΔG
ΔG0
-
+
ΔG0
RT ln Q
Самопроизвольная
реакция!
2NO2 = N2O4
pвнеш = pвнут , T = const
К = 25
K
pN2 O4
2
pNO
2
2
 pNO
2

 pN O
 2 4
2


f N2 O4
pNO2
  25  K  2  
f NO2  pN2O4
0


0
pвнеш = pвнут = pинерт (1-1000 бар)
pинерт >> pCO2 ,
T = 1000 K
p(CO2)= 1,3*10-7
p(CO2)= 1,7*10-7
Не
CaO (тв.) + CO2= CaCO3(тв.)
Практические константы равновесия в газе
2А + В = А2В
 p A2 B 
K p  K * 2 
 p A pB 
K p (Т );
0

d ln K p
dT
p A2 B
2
A
p pB
бар 
2
H

2
RT
0
Практические константы равновесия в идеальном газе
2А + В = А2В
0
p A2 B
 p A2 B 
2
2
K с  K *  2   RT   2  RT  
p A pB
 p A pB 
c A2 B
2
 2 М 
c A cB
d ln Kс Н  2 RT U


2
2
dT
RT
RT
0
Kс (Т );
0
Практические константы равновесия в разбавленном
растворе
Kс 
с A2 B
сс
2
A B
xA2 B
М   x x   
2
2
A B
pacт
2
 K *   pacт 
2
 d ln  раст 
H
 d ln K c 
K с (Т , p); 
 2

 
2
 dT  p RT
 dT
p

Cтандартное состояние С0 = 1М
  раст 
 c0 
1    RT ln x1  RT ln 
 RT ln  

 
c
раст
0





 c1  
 c1 
с

0
 1, x  RT ln 
 RT ln    1,c  RT ln  

 
c
c
раст
0
0






1, x




c


1 
1,c  lim  1  RT ln   
c1 0

 c0  
N2  3H 2  2 NH3
T  1000 K , 3n( N 2 )  n( H 2 )
p  pH 2  pN2  pNH3  1бар
K (298)  10 ; K (1000)  10
6
6
1
1
p ( H 2 )  7.4*10 , p( N 2 )  2*10 ,
p ( NH 3 )  2.5*10
4
{бар}
C2 H 4  H 2  C2 H 6
T  1000 K , n(C2 H 4 )  n( H 2 )
p  pC2 H 4  pH 2  pC2 H 6  1бар, K (1000)  8
pH2  0.25, pC2 H4  0.25, pC2 H6  0.5 {бар}
pH 2  0.9, pCH 4  0.1, Графит
6
6
pC2 H 4  1.2*10 , pC2 H 6  9*10 {бар}
«Изобара»
Квантовохимический расчет
T
H  H   c p dT
0
T
0
0
0
Cтат.термодинамика
T
S  S  
0
T
0
0
0
c p
T
Калориметрия
dT
G   RT ln K  H  T S
0
T
0
T
«Изотерма»
0
T
Для индивидуальных веществ…..
T
H  H   c p dT  H ф.п.
0
T
0
0
0
T
S S 
0
T
0
0
cp
0
T
T
Калориметрия
dT  Sф.п.
T
G  H   c p dT  T 
0
T
0
0
0
0
cp
T
dT
Третий закон термодинамики
H
0
 H 0 

  c p  0
 T  p
T 0
 G 
0

  S  0
 T  p
0
G
0
0
T
S  0 при T  0
Третий закон
Энтропия химических реакций и фазовых превращений
при Т0 стремится к нулю.
S0 =0
Энтропия всех кристаллических фаз стремится к
нулю при Т0 .
S0 =0
Фазовый переход в стеклообразное состояние
ср
Жидкость
II
∆сp
Стекло
I
Tg
Tпл
T
Неидеальный кристалл
S T  0   0
Для индивидуальных веществ…..
T
H  H   c p dT  H ф.п.
0
T
0
0
0
T
S  S 
0
T
0
0
0
cp
T
Калориметрия
dT  Sф.п.
G  H  TS 
0
T
0
T
T
0
T
T
H   c p dT  T 
0
0
0
0
cp
T
dT
Для индивидуальных веществ…..
Tпл
H T0  H 00 

c p (тв )dT  H пл.
0
Tкип


c p ( жд)dT ....
Tпл
Tпл
S 
0
T

c p (тв )
T
0
Tкип
dT  S пл. 
Tпл
G  H  H  H
0
T
0
0

0
T
0
0
  TS
0
T
c p ( жд)
T
dT ....
H
0
f ,0
TK
100
200
( A) 
cp
кДж / моль
H H
0
T
0
0
S
Дж / моль / К
0
T
G H

T
0
T
0
0