Lecture 1

Научные основы органического
синтеза
2014/15 уч. г., группа 4ГМ31
Лектор: Филимонов В.Д.
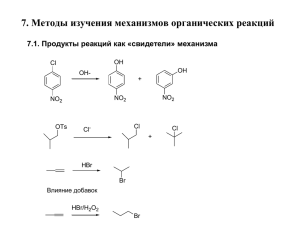
1. Профиль поверхности изменения свободной энергии
реакции
K
A + B
C
G
Термодинамика:
G = H - TS (уравнение Гиббса)
G = -RT ln K
Скорость реакции (кинетика):
k=Ae -G/RT Уравнение Аррениуса
G= H-TS Уравнение Гиббса
H=Ea – RT при 298К RT0 и HEa,
Ea энергия активации реакции
1
2
G 1
G 2
A+B
G
интермедиат
C
G = H - TS (уравнение Гиббса)
G = -RT ln K
H0 = S H0обр (продукты) – S H0обр (реагенты)
G0 = S G0обр (продукты) – S G0обр (реагенты)
Скорость реакции
k=Ae -G/RT Уравнение Аррениуса
G= H-TS Уравнение Гиббса
H=Ea – RT при 298К RT0 и HEa, где Ea называют энергией
активации реакции
Многостадийные реакции
A + B  [1]  [интермедиат]  [2]  С
+
[ CH2
медл.
CH2=CH2
+
[ CH2
+ HBr
-
-Br
CH2
+ 1
H]
[CH2CH3] + Br-
CH2
переходн. сост.1
[CH2CH3]
интермедиат
[ Br
+
2
CH2-CH3 ]
переходн. сост.2
[ Br
+
2
CH2-CH3 ]
+ 1
H]
Br-CH2-CH3
G1> G2 лимитирующая стадия - первая
Кинетическое описание механизма. Порядки реакций
Скорость= k [1]
CH3CH(Cl)CH2CH2CH2CH3 + NaOCH3 → CH3CH=CHCH2CH2CH3
2
Смесь изомеров
Скорость = k [2] [NaOCH3]
Скорость= k [CH3Li]1/4
Кинетические уравнения многостадийных реакций
Скорости последовательных стадий:
Стадия 1: d[C]/dt = k1[A] [B] – k-1 [C]
Стадия 2: d[D]/dt = k2[C]
Стадия 3: d[E]/dt = d[F]/dt = k3[D]
Проблема: концентрации промежуточных продуктов C и D, как правило, неизвестны.
Возможно ли узнать скорость, исходя из концентрации реагентов ?
Допущения:
1. первая стадия – быстро устанавливающееся равновесие и K< 1, т.е. k1 < < k-1
2. k2 << k3
Концентрация [C] связана с концентрациями [A] и [B] константой равновесия:
K = [C]/[A] [B]
k-1 = [C] = k1 [A] [B]
[C] = k1/k-1 ([A] [B])
Поэтому скорость второй стадии можно выразить через концентрации [A] и [B]:
d[D]/dt = k2 [C] = k2 ( k1/ k-1 ) ([A] [B]) = kнабл [A] [B]
Реакция первого порядка: k=1/t ln(c0/c)
Реакция второго порядка: k=1/t (a0 – b0) ln [b0(a)/ao(b)]
Где a, b и c относятся к концентрациям реагентов во время t, ao, bo и co – к
начальным концентрациям.
Приближение стационарного состояния
k1
A + B
C
k-1
C + D
k2
A + B + D
E + F
E + F
Если С – реакционноспособная нестабильная частица, то ее конц. никогда не будет
высокой и скорости образования и расходования интермедиата С примерно равны
k1 [A] [B] = k2 [C] [D] + k-1 [C]
k1[A][B]/(k2[D] + k-1) = [C]
Если вторая стадия лимитирующая, то:
Скорость = k2[C][D] = {k2k1[A][B])/(k2[D] + k-1)} [D]
Важные примеры кинетических уравнений органических
реакций
Реакции с быстрым равновесием
fast
k1
ROH + H+
RO+H2
k-1
+
-
RO H2 + Br
slow
k2
RBr + H2O
K = [RO+H2]/([ROH] [H+])
[RO+H2] = K [ROH] [H+]
Скорость = k2K[ROH] [H+] [Br-] = kнабл [ROH] [H+] [Br-]
Реакции ароматического нитрования
Экспериментально установлено, что скорость нитрования не зависит или почти не
зависит от концентрации бензола
Механизм 1
fast
k1
2 HONO2
H2O+NO2 + NO3-
k-1
H
+ H2O+NO2
slow
+
k2
H
NO2
NO2
fast
+
NO2
+ H+
Скорость = k2[H2O+NO2][C6H6] = (k2k1/k-1)([HONO2]2/[NO3-]) ([C6H6]) =
kнабл ([HONO2]2/[NO3-]) [C6H6]
Механизм 2
fast
k1
H2O+NO2 + NO3-
2 HONO2
k-1
+
H2O NO2
slow
NO2+ + H2O
k2
H
+ NO2+
H
fast
+
NO2
NO2
fast
+
NO2
+ H+
Скорость = (k2k1/k-1)([HONO2]2/[NO3-]) = kнабл ([HONO2]2/[NO3-])
Механизм 3
fast
k1
NO2+ + NO3- + H2O
2 HONO2
Скорость = k3 [7]
k-1
H
+ NO2+
NO2
Конц. интермедиата 7 можно
выразить через быстрое равновесие
k-2[7] = k2 [NO2+] [C6H6]
fast
k2
k-2
+
(7)
H
NO2
NO2
slow
+
k3
+ H+
7
[NO2+] = (k1[HNO3]2)/(k-1[NO3-][H2O])
Скорость = k3 ([C6H6] k1 [HNO3]2)/(k-2k-1[NO3-][H2O])
Скорость = kнабл [HNO3]2[C6H6]/NO3-][H2O]
Вывод: кинетическое уравнение по механизму 2 согласуется с экспериментальными
данными, которые показывают, что скорости нитрования бензола в растворителях не
зависит или почти не зависят от концентрации бензола. Однако могут существовать и
другие механизмы, которые подчиняются кинетическому уравнению
V = kнабл ([HONO2]2/[NO3-])
Таким образом, кинетика не дает абсолютно верного доказательства механизма реакции.
В дополнении к кинетике необходимы другие методы доказательств механизма !
OH
PhCH=O + PhCOCH3
slow
EtO-
fast
Ph
O
+ H2O
Ph
O
Ph
Скорость = kнабл [PhCOCH3] [-OEt] [PhCHO]
Ph
Предполагаемый механизм
O
+ -OEt
Ph
O
+ PhCH=O
O
+ EtOH
Ph
Ph
OH
O
+ -OEt
Ph
Ph
slow
k2
k-2
CH2
O
+ EtOH
k-1
CH3
Ph
O
fast
k1
Ph
O
O
Ph
fast
k3
k-3
CH2
Ph
OH
O
+ -OEt
Ph
Ph
O
fast
k4
+ -OH + EtOH
Ph
Ph
Какой кинетический закон должен наблюдаться, если этот механизм правилен ?
Скорость контролируется стадией 2, поэтому, принимая, что k2 >> k-2, можно записать
для общей скорости реакции
Скорость = k2 [PhCOCH2-][PhCHO]
Так как [PhCOCH2-] неизвестна, ее выражают через известные концентрации
[-OEt] и [PhCOCH3]. Эти три концентрации связаны между собой в силу
равновесия, устанавливающегося на первой стадии:
[PhCOCH2-] = K [PhCOCH3] [-OEt]
Таким образом
Скорость = k2 K [PhCOCH3] [-OEt] [PhCHO] =
= kнабл [PhCOCH3] [-OEt] [PhCHO]
Кинетическое уравнение согласуется с предложенным механизмом
Вклад энтропии активации в изменение свободной энергии
Очень часто вклад энтропийной составляющей TS в уравнении Гиббса G = H - TS
относительно невелик
Если поступательная, колебательная или вращательная степени свободы при
продвижении к переходному состоянию значительно теряются, тогда общая энтропия
системы будет сильно уменьшаться. Наоборот, с приобретением большой
поступательной, колебательной или вращательной степеней свободы будут
значительные положительные энтропии активации.
Примеры реакций со значимыми вкладами TS в изменения свободной энергии G:
Димеризация циклопентадиена
H = 15.5 ккал/моль,
S = -34 кал/моль*град
+
Bu-N=N-Bu → 2 Bu• + N2
H = 52 ккал/моль, S = +19 кал/моль*град
Разложение 1,1’-азобутана