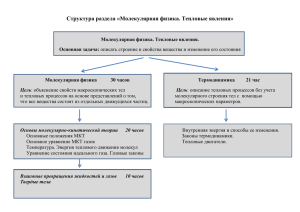
Эмпирические газовые законы (1)

Термодинамические параметры
I. Давление газа:
F
p 
S
Н
 p   м2  Па
F - суммарная сила, действующая по нормали к
поверхности
S - площадь поверхности
II. Объём газа:
V
V   м3
III. Абсолютная температура:
T
T   К
T  t  273,15 K
1C  1K
Эмпирические газовые законы (1)
Изопроцессы – процессы, протекающие в системе с
постоянной массой газа при каком-либо фиксированном
термодинамическом параметре.
I. p=const
Закон Гей-Люссака:
V  V0 (1  V t C ) , где
V  V0 ( t  0C )
температурный коэффициент объемного расширения:
V
1  V 
1




V0  T V
273
Эмпирические газовые законы (2)
II. V=const
Закон Шарля:
p  p0 (1   p t C) , где
p  p0 ( t  0C )
температурный коэффициент объемного расширения:
p
1  p 
1




p0  T V
273
III. T=const
Закон Бойля-Мариотта :
pV  const
Закон Авогадро
Равные объёмы различных газов при одинаковых давлениях и
температурах содержат одно и то же число молекул.
Количество вещества
N
m
 

NA
M
N A - число Авогадро
М - молярная масса
  
моль
1
N A  6,02  10
моль
23
Уравнение Менделеева-Клапейрона
m
PV 
RT
M
P
V
m
M
T
R
уравнение состояния идеального газа
- давление газа
- объём газа
- масса газа
- молярная масса газа
- абсолютная температура газа
- универсальная газовая постоянная
Дж
R  kN A
R  8,31
моль  К
P, V, T – параметры состояния системы
Закон Дальтона
pсмеси 
p
i
i
Давление смеси газов равно сумме их парциальных
давлений.
pi - парциальное давление – давление, которое
данный газ создавал бы в отсутствие остальных


pi    ni  kT  nсмеси kT  pсмеси

i
 i

Получим связь давления идеального газа с его
концентрацией и температурой
m RT
NA
p 

kT  nkT
M V
V

n
n - концентрация газа
k - постоянная Больцмана
Количество вещества смеси газов

 смеси 
i
i
 - количество вещества газов, входящих в состав
смеси
Молярная масса смеси газов
смеси 
m

i
i
i
i

m
i
i
mi

i
i
Основное уравнение МКТ
Nx
1
 nSvt
6
Основное уравнение МКТ
Основное уравнение МКТ
Средняя сила, действующая на стенку со стороны одной
молекулы:
Fx
vx
2m0v
  m0

t
t
Число ударов молекул о стенку за время t:
Nx
Давление газа:
Fx N x
p
S
1
 nSvt
6
2

m
v
1
2
0
2

 nm0v  n
3
3 
2


2
  n  пост

3

 пост - средняя кинетическая энергия поступательного движен
одной молекулы
Физический смысл температуры T
Уравнение
Менделеева-Клапейрона:
pV   RT
Основное уравнение
кинетической теории газа:
2
p  n
3
1
пост
N
2
RT  N
NA
3
1
пост
1
пост
3 R
3

T  kT
2 NA
2
k  1, 38  10 23 Дж К