Теория упругости и пластичности
реклама

Министерство образования Республики Беларусь
Учреждение образования
“Брестский государственный технический университет”
Кафедра сопротивления материалов и теоретической механики
УДК 539.3
ТЕОРИЯ УПРУГОСТИ И ПЛАСТИЧНОСТИ
методические указания и задания
к выполнению контрольной работы
для студентов специальности 1- 70 02 01 – “Промышленное и гражданское
строительство” факультета инновационной деятельности и финансов
0
q(x,y)
x
b
a
y
Брест 2014
УДК 539.3
Настоящие методические указания направлены на приобретение
студентами навыков самостоятельной работы при изучении курса
«Теория упругости и пластичности». В них приведены краткие теоретические сведения, примеры расчета и индивидуальные задания для
трех типов задач теории упругости: исследование напряженнодеформированного состояния в точке тела, плоская задача теории
упругости, расчет тонких пластин.
Составители: Веремейчик Андрей Иванович, доцент
Хвисевич Виталий Михайлович, доцент
Рецензент: директор филиала РУП «Институт БелНИИС»«Научно-технический центр», д-р техн. наук А.Я. Найчук.
Брестский государственный технический университет, 2014
2
СОДЕРЖАНИЕ
Общие положения ……………………………………………………….……
Требования к оформлению контрольной работы …………...…...................
Краткие теоретические сведения…………………...............…..…………….
Примеры решения задач…………………………………….………………...
Условие задания……………………………………………….………………
Литература…………………...…………………………………..…………….
3
3
3
20
54
65
ОБЩИЕ ПОЛОЖЕНИЯ
Методические указания соответствуют базовым учебным планам специальности 1- 70 02 01 – “Промышленное и гражданское строительство” и включают в себя краткие теоретические сведения, условия задания и примеры расчетов по исследованию напряженно-деформированного состояния в точке тела,
решению плоской задачи теории упругости, расчету тонких пластин.
Каждый студент-заочник по теории упругости и пластичности должен
выполнить одну контрольную работу. При защите контрольной работы необходимо ответить на вопросы по теме работы и уметь решать тестовые задачи
по ее тематике. Зачет по курсу принимается после того, как зачтена контрольная работа.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
1. Контрольная работа выполняется на отдельных листах формата А4 с рамкой
для текстовых документов.
2. Порядок оформления: титульный лист; задание с указанием исходных данных и схем конструкций; текст расчетов с необходимыми пояснениями и
схемами; перечень литературы.
3. Чертежи и схемы выполняются с соблюдением правил графики и масштабов
согласно стандарту УО «БрГТУ».
4. Текстовая часть выполняется в соответствии с требованиями к оформлению
текстовых документов. Страницы нумеруются. Расчеты выполняются в общем виде, подставляются значения величин, записывается числовой результат с указанием размерности полученной величины. Все вычисления производятся в десятичных дробях с точностью до сотых долей.
5. Эпюры необходимо строить на одном листе с расчетной схемой, на эпюрах
указывать числовые значения характерных ординат и единицы расчетных
величин.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Исследование напряженно-деформированного состояния в точке тела
В твердом теле, загруженном системой уравновешенных сил, происходит
взаимное перемещение точек, возникают линейные и угловые упругие деформации, что вызывает изменение сил взаимодействия между частицами тела.
Эти изменения в силах взаимодействия называют внутренними силами, а их
3
интенсивность на бесконечно малых площадках, проведенных внутри тела в
той или иной точке — напряжениями.
Если внутри загруженного тела вблизи некоторой точки вырезать бесконечно малых размеров параллелепипед (рисунок 1, а), то на его гранях можно
показать 9 компонент напряжений (рисунок 1 б, в). Совокупность этих 9 компонент полностью характеризует напряженное состояние в данной точке тела и
образует тензор Т , который записывается в виде такой матрицы :
T
x xy xz
y
yz .
yx
zx zy z
Нормальные напряжения считаются положительными, если они вызывают растяжение. Касательное напряжение считается положительным, если
на площадке, внешняя нормаль к которой совпадает с направлением параллельной ей координатой оси, оно направлено в сторону соответствующей этому направлению положительной координатой оси. Если внешняя нормаль противоположна направлению параллельной ей координатной оси, то положительное касательное напряжение направлено противоположно координатной
оси.
Зная компоненты напряжений на трех взаимно ортогональных площадках в некоторой точке тела, можно найти нормальную и касательную составляющие на любой другой площадке, проведенной через данную точку тела
( , ) (рисунок 1, в).
Известно что в любой точке тела всегда существуют по крайней мере три
такие взаимно ортогональные площадки, на которых отсутствуют касательные
напряжения, а нормальные напряжения достигают экстремума. Эти площадки
и напряжения называют главными (рисунок 1, г). Главные напряжения обозначают индексами 1,2,3, которые ставят в соответствии с неравенством
.
1
2
3
Площадки равнонаклонённые к главным, и напряжения, действующие на
них, называются октаэдрическими окт,окт (рисунок 2).
Наибольшие касательные напряжения действуют по площадкам, наклонных под углом 45 к каждой паре главных площадок, и равных полуразности
соответствующих главных напряжений. Их обозначают 12,23,31 (рисунок 2).
4
Рисунок 1.
a)
a)
3
3
октб)
октб)
3
3
окт
окт
окт
окт
1
1
2
2
октаэдр
октаэдр
Рис. 2.
2
2
1
1
l окт = m окт = n окт
l окт = m окт = n окт
Рисунок 2.
450
0
45
450
450
Рис. 3.
Рисунок
Рис. 3. 3.
5
Основные уравнения теории упругости:
I. Группа статических уравнений:
Дифференциальные уравнения равновесия (Навье - Коши):
x xy xz
X 0;
x
y
z
yx y yz
Y 0;
x
y
z
zx zy z
Z 0;
x
y
z
где X , Y , Z - объемные силы.
II. Группа геометрических уравнений:
Формулы Коши:
U
V
W
- линейные деформации: x
; y
; z
;
x
y
z
U V
V W
W U
- угловые деформации: xy
; yz
; zx
;
y x
z
y
x
z
где U ,V ,W - перемещения вдоль осей x,y,z соответственно.
Уравнения неразрывности (Сен-Венана):
2
2
xy zx yz
2 x
2 x y xy
2
;
2
;
x z
y
x
yz
y 2
x
xy
(1)
(2)
2 y
2
2 z yz
2
;
z 2
y
yz
2 y
yz xy zx
(3)
;
2
y x
z
y
zx
2 z 2 x 2 zx
zx yz xy
2 z
;
;
2
x 2
z 2
zx
z y
x
z
xy
III. Группа физических уравнений:
Обобщённый закон Гука:
- прямая форма:
1
1
1
x x y z ; y y z x ; z z x y ;
E
E
E
xy
E
,
2(1 )
- обратная форма:
xy
G
;
yz
yz
G
;
zx
zx
G
,
(4)
где G
x 2 x ;
xy G xy ;
y 2 y ;
yz G yz ;
z 2 z ;
zx G zx ;
(5)
6
E
Ev
;
– коэффициенты Ляме.
2 (1 v)
1 v 1 2v
Решение уравнений групп I, II, III должно быть при выполнении условий
на поверхности (3).
Cистема 15 уравнений (1), (2), (4) или (5) используется для определения
15 неизвестных ( x , y , z , xy , yz , zx , x , y , z , xy , yz , zx , U ,V ,W ).
где
Способы решения:
1. решение в перемещениях;
2. решение в напряжениях;
3. решение в системной форме.
Методы решения:
1. Прямой метод. Интегрируется система 15-ти уравнений при выполнении условий на поверхности.
2. Обратный метод. Задаются функции напряжений или перемещений,
удовлетворяющих системе уравнений. А затем из граничных условий
определяются нагрузки, соответствующие такому решению.
3. Полуобратный метод Сен-Венана. Часть неизвестных задаётся и представляется в систему уравнений, из которых определяются остальные
неизвестные.
Формулы и уравнения, по которым можно вычислить ,, главные
напряжения и их направление, окт, окт, 12, 23, 31, а также другие необходимые зависимости будут приведены ниже в примерах решения задач.
Плоская задача теории упругости
В теории упругости различают две плоские задачи (рассматривается плоскость xOy ):
1. Плоское деформированное состояние, при котором деформации из плоскости, т. е. в направлении оси z , равны нулю: z 0 , zx 0 , zy 0 . К этой задаче относится расчет тел, вытянутых вдоль оси z , под действием нагрузки, перпендикулярной оси z и постоянной вдоль нее (длинные пластины, подпорные
стенки, плотины).
7
z
a)
q
б)
z
x
0
y
0
x
1
q
y
Рисунок 4 – Примеры плоского деформированного состояния.
2. Обобщенное плоское напряженное состояние, при котором напряжения
из плоскости z , zx , zy равны нулю. К этой задаче относится расчет тонких
пластин, загруженных по боковым граням силами, параллельными плоскости
пластин (рисунок 5).
y
F
y
x
z
q
z=1
Рисунок 5 – Пример плоского напряженного состояния.
Суть обобщения: для пластин конечной толщины принимается то, что
выполняется в бесконечно тонкой пластине:
а) равенство нулю напряжений из плоскости;
б) равномерное распределение неизвестных напряжений x , y , xy по толщине пластин.
Основные уравнения для плоской деформации.
1) Уравнения равновесия:
x xy
X 0;
x
y
xy y
Y 0;
x
y
Условия на поверхности:
(6)
8
P l m,
x
x
xy
P l m;
y
yx
y
2) Формулы Коши:
u
v
u v
; ; ;
y y
xy y x
x x
Уравнение неразрывности:
2
2
2 x y xy
;
2
2
x
y
y
x
3) Закон Гука:
a) В прямой форме
21
1
1
x 1 y ,
y 1 x ,
;
x E
y E
xy
xy
E
1
1
б) В обратной форме
E
E
E
;
1 x 1 y , 1 y 1 x ,
xy 21 xy
x 1 2
y 1 2
E
;
где E
.
1 1 2
1 1
При плоском напряженном состоянии плоскости свободны от нагрузки:
0;
z
zx
yz
а другие напряжения не зависят от координаты Z:
( x, y); ( x, y ); ( x, y).
x
x
y
y
xy
xy
Из закона Гука:
x y ,
1
1
а x y , y x ,
y E
x E
E
E
x y ,
x ,
x 1 2
y 1 2 y
z
E
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
21
;
xy
xy
E
E
.
xy 21 xy
Таким образом, плоское напряженное состояние и плоская деформация
отличаются лишь постоянными E , E1 и , 1 при использовании закона Гука, и
обе задачи можно объединить в одну: плоскую задачу теории упругости.
В итоге для решения плоских задач имеем восемь уравнений: два уравнения Навье-Коши; три уравнения Коши и три уравнения обобщенного закона
Гука, с восьмью неизвестными: x , y , xy , U, V, x , y , xy .
9
При решении задачи в напряжениях основными неизвестными будут x ,
y , xy . Если объемные силы постоянны (например, собственный вес), то
уравнения для обеих плоских задач совпадают. Решение упрощается, если все
неизвестные напряжения выразить через одну функцию - ( x, y) - функцию
напряжений следующим образом :
2
2
2
x 2 ; y 2 ; xy
Xy Yx ,
(15)
y
x
xy
где X, Y – объемные силы, параллельные осям x и y соответственно.
Функцию ( x, y) можно определить из решения бигармонического уравнения:
4
4
4
2 2 2 4 0
(16)
x 4
x y
y
при граничных условиях:
X x xy m;
Y yx y m.
При определении значения угла между нормалью и осью, поворачиваем
нормаль против хода часовой стрелки до совмещения с положительным
направлением взятой оси.
Во многих случаях получить точное решение бигармонического уравнения плоской задачи теории упругости (16) оказывается сложным. Для приближенного решения этого уравнения применяют численные методы и в частности
метод конечных разностей (МКР).
Суть МКР состоит в том, чтобы решение плоской задачи с помощью
функции напряжений свести к алгебраическим уравнениям. В этом методе
частные производные бигармонического уравнения (16) приближенно заменяются конечными разностями, в результате чего оно превращается в алгебраическое. Это уравнение, как увидим далее, содержит значение функции напряжений в тринадцати точках, расположенных в определенном порядке на сетке вокруг центральной точки. Поэтому вместо одного бигармонического уравнения
в частных производных приходится составлять и решать систему линейных алгебраических уравнений. Точность МКР прямо зависит от густоты сетки: чем
гуще сетка, тем точнее будет решение задачи.
Рассмотрим некоторую функцию (x ) проходящую через точки 1, 2, 3
(риcунок 6). Представим приближённо эту функцию параболой
a x 2 b x c , тогда
лев
a 2 x b x c ;
c;
о
Находим коэффициенты a, b :
пр
a 2 x b x c .
10
a
лев 2о пр
2 2 x
,
с .
о
2x
Уравнение параболы примет вид:
a
,
x
2
1
лев
лев 2о пр
3
( x)
пр
Находим производные
2 2 x
пр лев
2
x
x c.
2x
пр лев
d лев 2о пр
x
,
2
dx
2
x
x
d 2 лев 2о пр
.
x
0
x
пр лев
x
Рисунок 6.
dx 2
2 x
При x 0 :
лев 2о пр
d 2
.
(б)
2
dx2
x
o
Воспользуемся этими формулами для решения плоской задачи. Нанесём на
пластину с шагом x и y (рисунок 7).
пр лев
d
;
dx
2
x
o
(а)
y
k
a
f
d
i
b
h
c
g
y
e
l
y
n
m
x
x
x
Рисунок 7.
Наметим некоторую центральную точку “i”. На основании формул (а) и
(б) для неё:
11
b d
;
2x
x i
2
x 2
2i d
b
;
2
x
i
a c
;
y
2
y
i
2
y 2
2i c
a
;
2
y
i
2
x a x c
xy
y x i
2y
i
f e g h
1 f e g h
.
2y
2x
2x
4xy
Используя (17), находим 4-ю производную:
4 6 4
b d
e n ;
i
4
4
x
x
i
4 6 4
a c
k m ;
i
4
4
y
y
i
(17)
(в)
4i 2 a b c d f e g h
4
.
2y 2
x 2y 2
x
i
Подставим (в) в (16) и после преобразования получим уравнение, заменяющее бигармоническое:
6 2 8 6i 4 1a b c d 2 e f g h
k 2l m 2n 0,
(18)
y 2
где
.
2
x
Напряжения в точке “i” получим по формулам:
2 2
i c;
a
x y 2
2 y
i
2 2
i d;
b
y x 2
2 x
i
(19)
12
2 e f g h
.
xy
xy
4xy
i
Уравнения (19) должны составляться для каждой внутриконтурной точки. Когда уравнения составляются для внутриконтурных точек, лежащих на
ближайшей линии параллельной контуру, то в них вынужденно входят и значения функции контурных и законтурных точек. Значения функции на
контуре и вне контура находят из граничных условий (рисунок 8). Таким образом, неизвестных значений столько, сколько узлов внутри контура.
k
y
y
q(x)
n
e
d
a
i
f
b
h
c
g
l
m
Рисунок 8.
Для определения значений функции на контуре и вне его удобно воспользоваться так называемой рамной аналогией (идеи профессоров П.Л. Пастернака, П.М. Варвака, А.П. Синицина). Если, например, на верхней грани
прямоугольной области приложена нагрузка g(x), направленная вниз, то для
этой грани можно записать
2
q .
y x2
Сравнивая это выражение с известной зависимостью
d2 M
q.
dx 2
заключаем, что функцию напряжений на контуре пластинки можно принять
за значение изгибающего момента в данной точке балки (рамы) с такой же
нагрузкой, т.e.
a Ma
или в общем виде:
KOH
M .
(20)
Для отыскания в законтурной точке k используется формула:
13
зак 2 N вн .
(21)
зак.
контур
вн.
Рисунок 9.
Рис.5.
Из формул (20) и (21) следует, что для записи кон и зак нужно построить
эпюры изгибающих моментов (M) и продольных сил (N) в соответствующей
раме. Под соответствующей рамой будем понимать такую раму, которая повторяет контур пластинки, геометрически неизменяемая и, желательно, статически
определимая.
На основании выше изложенного следует придерживаться следующего
порядка расчета балки-стенки (пластинки) методом конечных разностей:
1. На заданную балку-стенку наносится сетка с определенным шагом и нумеруются внутренние узлы сетки (с учетом симметрии).
2. В соответствии с методом рамных аналогий, выбирается соответствующая
рама и для нее строятся эпюры изгибающих моментов (M) и продольных сил
(N). Эпюра (M) строится на растянутых волокнах, изгибающие моменты, отложенные внутри контура рамы считать положительными. Знак продольной силы: растяжение плюс, сжатие минус.
3. Выражаются значения функции в законтурных точках через внутриконтурные по формуле (21).
4. Записываются алгебраические уравнения по формулам (18) для каждой
внутриконтурной точки.
5. Решается система уравнений и находятся значения функции в внутриконтурных точках.
6. Определяются напряжения в узлах сетки по формулам (19) и строятся их
эпюры.
Расчет тонких пластин
Пластинкой называется тело призматической или цилиндрической формы, у которого толщина мала по сравнению с другими размерами, т.е. hab
(рисунок 10).
Пластинки, которые будем рассматривать в данной работе, являются тонкими, жесткими, упругими и прямоугольными. Это значит, что толщина их h
не превышает 1/5 наименьшего размера в плане, а наибольший прогиб w не
превышает 1/4 толщины.
Задача о расчете пластинок является трехмерной, однако вследствие некоторых гипотез она сводится к двухмерной. Широкое практическое примене-
14
ние получила техническая теория изгиба на основе гипотез, предложенных
немецким физиком Г. Кирхгофом. Согласно этим допущениям, все напряжения
и деформации можно выразить через функцию прогибов срединной поверхности пластинки w(x, y).
Считаем, что пластинка находится под действием поперечной нагрузки,
т. е. нормальной к срединной плоскости, а срединная плоскость совпадает с
плоскостью xOy прямоугольной системы координат. Ось z направлена по вертикали вниз (рисунок 10). Начало координат (точка О) выбирается в зависимости от конкретной задачи.
Рисунок 10 - Схема пластинки.
Усилия в сечениях пластинки, нормальных к ее срединной плоскости,
выраженные через функцию прогибов w(x, y) (погонные, т. е. приходящиеся на
единицу ширины сечения) определяются по формулам:
2w
2w
2w
2w
M x D 2 2 ,
M y D 2 2 ,
x
y
x
y
2w
M xy M yx D 1
,
xy
(22)
3w
3w
3w
3w
Qx D 3
Qy D 3
;
.
x y 2
y x 2
x
y
где M x , M y - погонные изгибающие моменты в сечениях с нормалью x и y со-
ответственно; M xy M yx - погонные крутящие моменты в тех же сечениях;
Eh3
- цилинQx , Qy - погонные перерезывающие (поперечные) силы; D
2
12(1 )
дрическая жесткость при изгибе.
Напряжения связаны с Мx, My, M xy M yx , Qx , Qy следующим образом:
15
Q S
Q S
y y
x
x
;
;
x
z; y
z; xy
z;
zx
zy
J
J
J
J
J
My
Mx
M xy
(23)
где J h - погонный момент инерции сечения пластинки, S S 1 h z 2 x y 2 4
12
2
3
статический момент отсеченной части площади сечения.
Эти формулы аналогичны формулам, полученным в сопротивлении материалов при изгибе балки прямоугольного сечения шириной, равной единице.
Действие силовых факторов и распределение напряжений в сечениях
пластинки показаны на рисунках 11, 12, 13.
x
y
x
Mx
My
h
y1
y
x 1
Рисунок 11 - Эпюры нормальных напряжений x , y .
yx
Эпюра
yx
x
Эпюра
Myx
max
Qy
y1
y
y
x
Qx
zy
zy
Mxy
h
zx
max
zx
y1
x 1
x 1
Рисунок 12 - Эпюры касательных напряжений yx , xy , zx , zy .
Примечание. На рисунках 11, 12, 13 показаны положительные направления указанных
усилий.
Из формул (22) и (23) следует, что для определения усилий и напряжений
необходимо знать функцию прогибов w(x, y), которая должна в каждой точке
пластинки удовлетворять следующим требованиям:
а) основному дифференциальному уравнению ее изогнутой поверхности
(уравнению Софи Жермен);
б) условиям на опорном контуре (граничным условиям).
Уравнение Софи Жермен имеет вид:
16
4w
x4
2
4w
x 2y 2
4w
y4
q
q
4
, или w ,
D
D
(24)
где - оператор Лапласа, q(x, y)— распределенная нормально к поверхности
пластинки нагрузка.
Укажем, каковы должны быть граничные условия для функции w(x, y) в
различных случаях закрепления пластинки (рисунок 13).
Шарнирное закрепление
x
Защемленный
край
b
Свободный
край
а
y
Рисунок 13 - Варианты закрепления граней пластинки.
Для каждого края пластинки должно быть два граничных условия.
1. Защемленный край:
w
при x=0: прогиб w=0, угол поворота
0 .
x
2. Шарнирно опертый край:
2w
2w
при y=0: прогиб w=0, изгибающий момент M y D 2 2 0 .
x
y
3. Свободный край:
2w
2w
при x=a: изгибающий момент M x D 2 2 0 , приведенная
y
x
3w
3w
поперечная сила Q D 3 2
.
2
x
x
y
Здесь рассмотрены три основные способа закрепления краев пластинки
(защемленный, опертый и свободный края) и показаны соответствующие граничные условия для функции w. На практике приходится встречаться и с другими способами закрепления. Например, встречается такое закрепление края
пластинки, когда прогиб по краю невозможен, поворот же края возможен, но
сопровождается появлением изгибающих моментов пропорциональных повороту — упруго заделанный край ( w 0, 0, M 0 ). Иногда край пластинки
опирается не на жесткий контур, а на какую-либо балку — упруго опертый
край ( w 0, Q 0 ). Возможны и другие способы закрепления. Составление
прив
x
17
граничных условий для различных случаев, на основании того, что было сделано для трех основных способов закрепления, не представит никаких трудностей.
Задача об изгибе пластинки будет решена, если будет найдена функция
w(x, y), удовлетворяющая уравнению (24) и граничным условиям. Эта задача в
некоторых случаях решается обратным методом, т. е. задается вид функции
прогибов w(x, y), а затем определяются нагрузки и условия закрепления, которым соответствует эта функция.
Очень часто, когда не удовлетворяется уравнение (24), расчет производится приближенным методом Бубнова-Галеркина. Он состоит в том, что для
заданной нагрузки q(x, y) задается вид функции w(x, y), удовлетворяющей только граничным условиям. При подстановке w(x, y) и q(x, y) в уравнение Софи
Жермен последнее может тождественно (для всех точек пластинки) не удовлетворяться. Поэтому уравнение удовлетворяют в среднем для всей площади пластинки, т. е. в интегральном смысле. Исходя из этого, получают следующее
уравнение Бубнова-Галеркина:
q
2 2
( w) wdS wdS ,
S
SD
где S — плоская область, ограниченная контуром пластинки.
Задача об изгибе круглой пластины будет осесимметричной, если нагрузка
и условия закрепления её краев не зависят от полярного угла . В этом случае
прогибы также не зависят от угла , а являются функцией координаты r, т.
е. W f (r ) . Тогда имеем:
a) Дифференциальное уравнение равновесия
d 4 w 2 d 3w 1 d 2 w 1 dw q(r )
.
(25)
dr 4 r dr 3 r 2 dr 2 r 3 dr
D
б) Внутренние силы:
изгибающие моменты
d 2 w dw
1 dw
d 2w
M r D( 2
), M D(
2 ),
dr
r dr
r dr
dr
поперечная сила
Qr D(
d 3w 1 d 2 w 1 dw
).
dr 3 r dr 2 r 2 dr
в) Граничные условия:
dw
0,
dr
dw
d 2 w dw
шарнирное закрепление - w 0;
0; M r D( 2
) 0,
dr
dr
r dr
жесткое защемление - w 0;
18
свободный край (в зависимости от действующих нагрузок) - M r 0 или
M r m, Qr 0 или Qr F .
Уравнение (25) можно решить в общем виде w w1 w2 , где w1 - общее решение однородного уравнения , w2 - частное решение неоднородного уравнения:
w1 C1 C2 ln r C3 r 2 C4 r 2 ln r .
Например, для равномерно распределённой нагрузки q(r ) q const :
qr 4
qr 4
.
Тогда
Постоянные
w
C1 C2 ln r C3 r 2 C4 r 2 ln r .
64D
64 D
C1 , C2 , C3 , C4 определяются из граничных условий.
Рассмотрим сплошную пластинку, шарнирно опёртую по контуру и
нагруженную равномерно распределенной нагрузкой интенсивности q.
w2
a
x
0
y
q
r
0
0
0.206qa2
2
0.088qa
0.088qa2
0.206qa2
Рисунок 14.
Для определения постоянных С1, С2, С3, С4 имеем следующие условия: в
центре пластинки при r=0 прогиб w должен иметь конечное значение. Т.к.
ln 0 , то С2=С4=0. Решение имеет вид:
qr 4
w(r )
C1 C3r 2 .
64 D
Определим С1 и С3; при r=a должно быть w=0; Mr=0.
Из первого условия (w=0):
19
qa 4
C1 C3a 2 0 .
64 D
Из второго условия (Mr=0):
3qa 2 v
qa 3
2C3
C3 2a
0 , откуда
16 D a
16 D
5 v qa 4
3 v qa 2
C1
; C3
.
1 v 64 D
1 v 32 D
Подставляем полученные величины в выражение для w(r ) :
q(a 2 r 2 ) 5 v 2
w(r )
a r2 ,
64 D 1 v
Подставляем функцию w(r ) в выражения для Mr и Mθ, получим:
q
M r (3 v)(a 2 r 2 );
16
q
M (3 v)a 2 (1 3v)r 2 .
16
Эпюры Mr и Mθ построены при v 0,3 (рисунок 14).
В случае сплошной защемлённой по контуру пластинки при действии
равномерно распределенной нагрузки для определения постоянных С1 и С3
имеем следующие граничные условия: на контуре пластинки должны отсутствовать прогибы и углы поворота сечений.
dw
При r a : w 0;
0.
dr
2
q
Окончательно получим: w(r )
a2 r 2 .
64 D
Для кольцевой пластинки с защемлённым наружным краем для определения постоянных С1, С2, С3, С4 в функции w(r ) , имеем следующие граничные
условия:
dw
При r=a: w 0,
0.
dr
При r=b: M r 0; Qr 0.
Подставляя в эти условия w(r ) , получим четыре уравнения для определения постоянных. Дальнейшие вычисления не представляют трудностей.
Вопросы для самопроверки.
1. Тензор напряжений T , его компоненты.
2. Определение полного P , нормального и касательного напряжения.
Условия на поверхности.
3. Определение величины главных напряжений и положения главных площадок.
20
4. Проверка ортогональности главных площадок.
5. Максимальные касательные напряжения max .
6. Октаэдрические площадки и напряжения окт, окт.
7. Построение круга Мора.
8. Тензор деформации T . Относительное изменение объема .
9. Обобщенный закон Гука.
10.Разложение тензора напряжений на составляющие T0 и D (аналитическое и графическое изображение).
11.Удельная потенциальная энергия деформации.
12.Определение расчетных напряжений по теориям прочности.
13.В чем сущность метода конечных разностей?
14.Какая разница между плоской деформацией и обобщенным плоским состоянием?
15.Напишите основное уравнение плоской задачи теории упругости.
16.Какие вы знаете методы решения плоской задачи теории упругости?
17.Какая функция называется бигармонической?
18.Дифференциальные уравнения равновесия для плоской задачи.
19.Условия на контуре для плоской задачи.
20.Как определяются напряжения X, Y, XY через функцию напряжений?
21.Каким требованиям должны удовлетворять напряжения X, Y, XY и
функциям напряжений ?
22.Какой вид имеет уравнение, которое записывается для внутриконтурных
точек?
23.Что такое x, y, ?
24.Как определить напряжения X, Y, XY в любой точке сетки МКР?
25.Для чего строятся эпюры изгибающих моментов и продольных сил?
26.Что такое соответствующая рама и требования, предъявляемые к ней?
27.Как определить значения функции напряжений на контуре балки-стенки?
28.Как выразить значения функции напряжений в законтурных точках?
29.Сколько необходимо составить уравнений МКР для решения плоской задачи теории упругости?
30.От чего зависит точность решения задачи МКР?
31.Что называется пластинкой?
32. Гипотезы теории изгиба тонких пластинок.
33.Какая пластинка называется тонкой?
34.Вид основного дифференциального уравнения изгиба пластинок?
35.Как выражаются внутренние силы в пластинке через функцию прогибов?
36.Формулы для напряжений в пластинке через внутренние условия?
37.Типы закрепления пластинок и граничные условия, которые соответствуют им.
38.Сущность метода Бубнова-Галеркина.
39.Условие прочности для определения толщины пластинки.
21
40.Сколько нужно граничных условий для каждого края пластинки и почему?
41.Что такое цилиндрическая жесткость пластинки?
42.Какую аналогию можно установить между уравнением изогнутой поверхности пластинки и бигармоническим уравнением плоской задачи?
43.В чем заключается сущность методов расчета пластинок Навье и Мориса
Леви?
44.Какие внутренние усилия возникают в пластинке при изгибе?
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
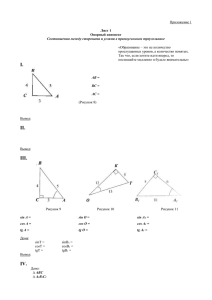
Пример 1.
Заданы компоненты напряжения на гранях элемента, вырезанного в некоторой точке загруженного тела. Стрелки на рисунке соответствуют положительным направлениям компонент в выбранной системе координат.
x 100 МПа; y 45 МПа; z 50 МПа;
xy 20 МПа; yz 30 МПа; zx 40 МПа.
Элементарный параллелепипед с заданными компонентами напряжения
представлен на рисунке 15.
z
50
30
40
40
20
100
45
20
x
30
y
Риунок 15 - Исходное напряженное состояние в точке.
Тело изотропно, материал подчиняется закону Гука. Модуль продольной
упругости Е = 200 ГПа = 2∙105 МПа; коэффициент Пуассона = 0,3.
Положение некоторой площадки, наклоненной к осям x, y, z и отсекающей от элементарного параллелепипеда тетраэдр (см. рисунок 1, в), задано
направляющими косинусами нормали к этой площадке l = cos =1/ 2 = 0,707;
m = cos =1/ 3 = 0,577; n = cos = 1/ 6 = 0,408. Как известно из математики,
направляющие косинусы должны удовлетворять условию l2+m2+n2=1.
Требуется:
1) Найти нормальную и касательную составляющие напряжений на площадке с
заданной ориентацией (с заданными направляющими косинусами l, m, n);
2) Определить величину и направление главных напряжений;
22
3) Найти величину наибольших касательных напряжений в данной точке тела и
указать площадки, по которым они действуют;
4) Найти нормальные и касательные напряжения на октаэдрических площадках
и указать их расположение;
5) Построить для заданного напряженного состояния круги Мора и указать на
них точки, изображающие напряженное состояние на площадках, на которых
напряженное состояние задано или определилось в процессе выполнения работы (площадках с нормалями x,y,z ; площадке с нормалью н, заданной направляющими косинусами l, m, n; октаэдрической площадке; площадках с максимальными касательными напряжениями; главных площадок);
6) Определить компоненты деформаций в заданных и главных осях;
7) Определить интенсивность напряжений и деформаций в рассматриваемой
точке;
8) Разложить заданный тензор напряжения на шаровой и девиатор;
9) Найти удельную потенциальную энергию деформации (полную, изменения
объема, изменения формы);
10) Определить расчетные напряжения по четырем классическим критериям
прочности и пластичности.
Решение:
1. Определение нормальной и касательной составляющих напряжения на площадке с заданной ориентацией.
Напряжения на площадке, нормаль к которой имеет направляющие
косинусы l, m, n, определяются из условий равновесия тетраэдра, отсекаемого
этой площадкой с нормалью от элементарного параллелепипеда с гранями, загруженными заданными компонентами напряжения (рисунок 16).
Составляющие вдоль осей x, y, z полного напряжения на площадке с нормалью определяются зависимостями:
pxvн x l xy m xz n ;
(26)
p yv yx l y m yz n ;
н
pz н zx l zy m z n .
Полное напряжение на площадке с нормалью :
p px2 н p y2 y pz2 н .
(27)
Нормальное и касательное напряжение на площадке с нормалью :
н px н l py н m pz н n xl 2 y m2 z n2 2 xylm 2 yz mn 2 zxnl ;
p2н 2н 2н ;
p2 2 .
н
н
н
(28)
(29)
23
Рисунок 16 - Напряжения на наклонной площадке.
Подставляя в зависимости (26) - (29) исходные данные, получаем составляющие вдоль осей x,y,z полного напряжения на площадке с нормалью н:
px = 100∙0,707+ 20∙0,577 + 40∙0,408 = 98,56 МПа;
p y = 20∙0,707 + 45∙0,577 + 30∙0,408 = - 24,07 МПа;
p z = 40∙0,707 30∙0,577 + 50∙0,408 = 31,37 МПа.
Полное напряжение на той же площадке :
p = 98,562 (24,07) 2 31,37 2 106,2 МПа.
Нормальное и касательное напряжения на площадке с нормалью :
= 100∙(1/ 2 )2 + (-45)∙(1/ 3 )2 + 50∙(1/ 6 )2 + 20∙1/ 2 ∙1/ 3 +
+ (-30)∙1/ 3 ∙1/ 6 + 40∙1/ 6 ∙1/ 2 = 68,6 МПа;
106,22 68,62 81,07 МПа.
2. Определение величины и направления главных напряжений.
Для отыскания величины главных напряжений необходимо решить кубическое уравнение:
3 I1 2 I 2 I3 0 .
(30)
Для отыскания величин главных напряжений вычисляем инварианты
напряженного состояния:
I1 x y z =100 - 45 + 50 = 105 МПа ,
I 2 x y y z z x xy2 yz2 zx2 100 (-45)+(-45) 50+50 100-20 2
-(-30) -40 =-4650 МПа ,
2
2
2
(31)
x xy xz
I 3 yz y yz x y z 2 xy yz zx x yz2 y zx2 z xy2
zx zy z
=-100 (-45) 50 +2 20 (-30) 40 - 100 (-30) 2 +45 402 - 50 202 =-311000 (МПа)3 .
24
Кубическое уравнение (5) принимает вид :
3 - 105 2 - 4650 +311000 = 0.
Кубическое уравнение (30) решаем с помощью формулы Кардано, относящейся к уравнению вида :
x 3 + c x + q = 0.
(32)
Это кубическое уравнение имеет три действительных корня, если выполняется неравенство :
D = (c/3)3 + (q/2)2 < 0.
(33)
Тогда решение кубического уравнения (32) запишется в виде :
x1 = - 2R cos(/3),
x2 = - 2R cos(/3 + 2/3),
(34)
x3 = - 2R cos(/3 + 4/3),
c
q
R
,
,
(35)
2 R3
3
при этом знак R должен совпадать со знаком q, а с 0.
Кубическое уравнение (30) можно привести к виду (32) посредством замены переменной
= x + I1 / 3.
(36)
Тогда
с = - I1 2 / 3 + I 2 ,
q = - (2 I13) / 27 + I1 I2 / 3 - I3.
(37)
Подставляя в (37) подсчитанные выше значения инвариантов напряжения
I1 , I2, I 3, находим
1052
c=-4650 =-8325 (МПа) 2,
3
2
105 (-4650)
q= 1053 +
+311000=62500 (МПа) 3.
27
3
Проверяем условия (10) и (12) :
3
2
-8325 62500
10
D=
+
= - 2,039 10 < 0 ,
3 2
C = -8325 < 0.
Оба условия выполнены. Следовательно, в данном случае можно воспользоваться решением Кардано:
8325
= 52,678 МПа,
R=+
3
cos= 62500/(2∙52,678)3 = 0,214, откуда = 1,355 рад.
По формулам (34) находим корни уравнения кубического уравнения
(32):
1,355 = - 94,791 МПа,
x1 =-2 52,678 cos
3
где: cos
25
1,355 2 = + 87,219 МПа,
x2 = -2 52,678 cos
3
1,355 4 = + 7,572 МПа.
x 3 =-2 52,678 cos
3
По формуле (36) найдем три корня уравнения (32), т.е. искомые значения
главных напряжений:
I
105
I = x1 + 1 = - 94,791+
=-59,791 МПа,
3
3
I
105
II = x 2 + 1 = 87,219+
=122,219 МПа,
3
3
I
105
III = x 3 + 1 = 7,572+
=42,572 МПа.
3
3
В соответствии с правилом 1 2 3 наибольшему по алгебраической
величине из этих напряжений присвоим индекс 1 и т. д. Тогда
1= II=122,219 МПа, 2=III=42,572 МПа, 3=I= - 59,791 МПа.
Для проверки правильности полученного решения найдем инварианты
напряженного состояния, выразив их через главные напряжения. Они должны
быть такими же, как и вычисленные выше по заданным компонентам напряжений (31):
I1 = 1 + 2 + 3 = 122,219+42,572 - 59,791 = 105 МПа,
I2 = 1 2 + 2 3 + 3 1 =122,219 42,572+42,572 (-59,791) +
+(-59,791) 122,219=-4649,91 МПа ,
I3 = 1 2 3 =122,219 42,572 (-59,791) =-311099 (МПа)3.
Положение главных площадок определяется направляющими косинусами
нормалей к главным площадкам. Для отыскания направляющих косинусов
нормали к i-той главной площадке (i=1,2,3) используем систему уравнений,
подставив в нее =i . Тогда направляющие косинусы принимают значение li ,
mi, ni.
x i li xy mi xz ni 0,
2
yx li ( y i ) mi yz ni 0,
(38)
zx li zy mi ( z i ) ni 0,
li2 mi2 ni2 1 .
(39)
Из трех уравнений (38) выберем любые два, например первое и второе. Делим эти уравнения на ni и вводим обозначения
ai = l i / n i ;
bi = m i / n i .
(40)
Получаем
x i ai xy bi xz ,
yx ai ( y i ) bi yz ,
26
отсюда
ai [ yx zy zx ( y i )] / [( x i )( y i ) xy2 ],
bi [ xy zx zy ( x i )] / [( x i )( y i ) xy2 ].
Тогда из (39) и (40)
1
li ai ni , mi bi ni ,
ni
,
1 ai2 bi2
(41)
(42)
Примем сначала: i = 1 = 122,22 МПа, и из (41) и (42) найдем :
ai = [20∙(-30) - 40∙(-45 – 122,22)]/[(100 – 122,22)∙(-45 – 122,22) - 202] = 1,836,
bi = [20∙40 - (-30)∙(100 – 122,22)]/[(100 – 122,22)∙(-45 – 122,22) - 202] = 0,040,
1
n1
0,478,
2
1 1,836 0,0402
l1 a1 n1 =1,836 0,478 0,878,
m1 b1 n1 0,040 0,478 0,019.
Проверка:
0,8782 + 0,0192 +0,4782 = 1,000.
l12 m12 n12 1,
Равенство выполнено.
Теперь подставляем в (41) и (42) 2 = 42,57 МПа и находим
a2 = [20∙(-30) - 40∙(-45 – 42,57)]/[(100 – 42,57)∙(-45 – 42,57) - 202] = - 0,535,
b2 = [20∙40 - (-30)∙(100 – 42,57)]/[(100 – 42,57)∙(-45 – 42,57) - 202] = - 0,465,
1
n2
= 0,816,
1 (0,535)2 (0,465)2
l2 a2 n2 = 0,535 0,816 0,437,
m2 b2 n2 0,465 0,816 0,379.
Проверка:
l22 m22 n22 1,
(-0,437)2 + 0,8162 +(-0,379)2 = 1,000.
Равенство удовлетворено.
Подставив в (41) и (42) 3 = -59,79 МПа, получаем:
a3 = [20∙(-30) - 40∙(-45 + 59,79)] / [(100 + 59,79)∙(-45 + 59,79) - 202] = - 0,607,
b3 = [20∙40 - (-30)∙(100 + 59,79)] / [(100 + 59,79)∙(-45 + 59,79) - 202] = 2,849,
1
n3
= 0,325,
1 0,607 2 2,8492
l3 a3 n3 = 0,607 0,325 0,197,
m3 b3 n3 2,849 0,325 0,926.
Проверка:
(-0,197)2 + 0,9262 +0,3252 = 1,002 1.
l32 m32 n32 1,
Сведем найденные значения в таблицу 1.
27
Таблица 1. Направляющие косинусы нормалей к главным площадкам.
i
1
li
0,878
0,437
0,297
mi
0,019
0,379
0,926
ni
0,478
0,816
0,345
2
3
Сделаем следующие три проверки, подтверждающие взаимную ортогональность главных площадок:
l1 l2 + m1 m2 + n1 n2 = 0;
0,878 ∙ (-0,437) + 0,019 ∙ (-0,379) + 0,478 ∙ 0,816 = -8,39∙10 -4 0;
l2 l3 + m2 m3 + n2 n3 = 0;
(-0,437) ∙ (-0,197) + (-0,379) ∙ 0,926 + 0,816 ∙ 0,325 = 3,35∙10 -4 0;
l1 l3 + m1 m3 + n1 n3 = 0;
0,878 ∙ (-0,197) + 0,019 ∙ 0,926 + 0,478 ∙ 0,325 = 2,20∙10 -4 0.
Можно сделать вывод, что взаимная ортогональность нормалей к главным площадкам этими проверками подтверждается.
Чтобы изобразить графически положение в пространстве параллелепипеда, гранями которого являются главные площадки, надо произвести следующее
построение.
Z
a)
2
-1
1
-
n2
m2
l2
n1
--1
l3
3
0
n3
l1
1
X
m1
m3
- 1
Y
1
= 122.22 МПа
б)
3
= -59.79 МПа
2
= 42.57 МПа
Рисунок 17 - Графическое построение главных площадок.
28
В осях x,y,z по заданным направляющим косинусам (таблица 1) строим
нормали к главным площадкам, взяв за исходную точку начало координат. Для
построения i-той нормали достаточно вдоль осей x ,y, z отложить в некотором
масштабе отрезки, равные направляющим косинусам li, mi, ni, и точку с такими
координатами соединить с центром О (рисунок 17, а). Его грани и будут главными площадками с напряжениями 1 , 2 , 3 .
3. Определение максимальных касательных напряжений.
Наибольшие касательные напряжения действуют по площадкам, наклоненным под углом 45 между каждой парой главных площадок (рисунок 3).
Величины наибольших касательных напряжений определяются по формулам:
13
1 3
2
;
12
1 2
;
2
23
2 3
2
;
(43)
13 = [122,22 - (-59,79)] / 2 = 91,01 МПа; 12 = [122,22 – 42,57)] / 2 = 39,83 МПа;
23 = [42.57 - (-59,79)] / 2 = 51,18 МПа;
max = 13 = 91,01 МПа.
Максимальное касательное напряжение действует по площадке, наклоненной под углом 45 к первой и третьей главным площадкам.
4. Определение октаэдрических площадок.
Площадки равнонаклонённые к трем главным площадкам l=m=n=1/ 3 ,
называются октаэдрическими (рисунок 2). Нормальное и касательное напряжения на этих площадках определяются по формулам:
окт ( 1 2 3 ) / 3;
(44)
2
12 22 32 1 2 2 3 3 1 ,
3
1
2 2
или окт
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
12 232 312 .
3
3
В данном случае:
1
окт = (122,22 + 42,57 - 59,79) = 35 МПа,
3
2
окт
39,832 52,182 91,012 74,50 МПа.
3
5. Построение кругов Мора.
В координатах и построим круги Мора для исследуемого объёмного
напряжённого состояния. Отложим в осях и точки, изображающие напряK1 ( 1 ,0) K1 (122,22;0);
жённое состояние на главных площадках:
K 2 ( 2 ,0) K 2 (42,57;0); K3 ( 3 ,0) K3 (59,79;0) (рисунок 18).
На отрезках K1 K 3 , K1 K 2 , K 2 K 3 , как на диаметрах строим окружности — это
и есть круги Мора для заданного напряжённого состояния.
окт
29
МПа
100
K13
80
60
Ky
*
K23
* Kокт
K12
* Kz
Kx
*
40
20
-60
-40
0
-20
-20
20
O2
K2
O1
O3
K3
40
80 100 120
60
K1
140
МПа
-40
-60
-80
-100
2=42.57
3 = - 59.79
1 = 122.22
Рисунок 18 - Круги Мора.
Напряженное состояние на любой площадке, проходящей через заданную
точку тела, изображается точками, которые лежат внутри заштрихованной области.
Нанесем на круги Мора точки, изображающие напряженное состояние на
площадках с нормалями x, y, z. Для этого на этих площадках найдем полные
касательные напряжения :
2
2
x xy
xz
202 402 44,72 МПа;
2
2
y yx
yz
202 30 36,06 МПа;
2
2
z zx2 yz
402 (30)2 50,00 МПа;
Координаты точек, изображающих напряженное состояние на площадках, перпендикулярных осям x,y,z :
K x ( x , x ) K x (100;44,72), K y ( y , y ) K y (45; 36,06),
K z ( z , z ) K z (50; 50).
30
Координаты точки, изображающей напряженное состояние на октаэдрической площадке:
K окт ( окт ; окт ) K окт (35; 74,5).
Точки, изображающие напряженное состояние на площадках с наибольшими касательными напряжениями K12, K23, K13, расположены на концах вертикальных диаметров кругов Мора. Все нанесенные в масштабе точки, изображающие напряженное состояние на всех рассмотренных площадках, действительно расположились внутри заштрихованной области (рисунок 18).
6. Определение компонент тензора деформации в заданных и главных осях и
относительного изменения объема.
Тензор деформации в заданных осях имеет вид:
1
1
xy
xz
x
2
2
1
1
(45)
T yx
y
yz .
2
2
1
zx 1 zy
z
2
2
Его компоненты находим по формулам обобщённого закона Гука в произвольных осях:
1
xy
x [ x ( y z )];
xy
;
E
G
1
yz
y [ y ( z x )];
yz
;
(46)
E
G
1
z [ z ( x y )];
zx zx ,
E
G
где G – модуль упругости при сдвиге;
E
2 105
G
7,69 104 МПа.
2 (1 ) 2 (1 0,3)
В нашем случае:
1
x
[100 0,3 (45 50)] 49,25 105 ;
5
2 10
1
y
[45 0,3 (50 100)] 45 105 ;
5
2 10
1
z
[50 0,3 (100 45)] 16,75 105 ;
5
2 10
20
30
40
xy
26 105 ; yz
39 105 ; zx
52 105.
4
4
4
7,69 10
7,69 10
7,69 10
Таким образом:
31
13
26
49,25
13
45 19,5 105.
26
19,5 16,75
Тензор деформации в главных осях:
1 0 0
Т 0 2 0 ,
(47)
0 0 3
где 1 , 2 , 3 — главные деформации, определяемые по формулам:
1
1
1
1 [ 1 ( 2 3 )]; 2 [ 2 ( 3 1 )]; 3 [ 3 ( 1 2 )]. (48)
E
E
E
В нашем случае:
1
1
[122,22 0,3 (42,57 59,79)] 63,69 105 ;
5
2 10
1
2
[42,57 0,3 (59,79 122,22)] 11,92 10 5;
5
2 10
1
3
[59,79 0,3 (122,52 42,52)] 54,61 10 5.
5
2 10
0
0
63,69
0
11,92
0 10- 5 .
0
0
54,61
Проверка: x y z 1 2 3 — первый инвариант деформированно-
го состояния.
( 49,25 - 45 + 16,75)∙10-5 = ( 63,69 + 11,92 – 54,61)∙10-5 ;
21∙10-5 = 21∙10-5.
Относительное изменение объема определяется по формуле
1 2 3 .
(49)
В данном примере
63,19 11,92 54,61 105 21 105.
Примечание: От деформаций по направлению осей x, y, z можно перейти к главным деформациям и определить их величины из кубического уравнения:
3 E1 2 E2 E3 0 ;
где: инварианты тензора деформаций: E1 x y z ;
1
1
1
E2 x y y z z x xy2 yz2 zx2 ;
4
4
4
1
1
1
1
E3 x y z xy yz zx x yz2 y zx2 z xy2 .
4
4
4
4
Решение данного уравнения проводится аналогично методике, изложенной в п. 2 примера.
7. Определение интенсивности напряжений и деформаций.
32
Интенсивность касательных напряжений определяем по формуле:
2
2
1
2
И
x y y z z x 6 xy2 yz2 zx2
6
2
1
2
2
100 45 45 50 50 100 6 202 ( 30) 2 40 2
6
91,241 МПа.
Интенсивность нормальных напряжений определяем по формуле:
2
2
1
2
И
x y y z z x 6 xy2 yz2 zx2 3 И
2
=158,035 МПа.
Интенсивность деформаций сдвига:
2
2
2
3 2
2
2
2
И
9,033 104 .
x
y
y
z
z
x
xy
yz
zx
3
2
Интенсивность продольных деформаций:
1
9,033 104
И
И
5,215 104 .
3
3
2
Строим направляющий тензор деформаций: Д
Д , где Д - девиа-
И
тор деформаций:
x 0
1
Д yx
2
1
zx
2
,
z 0
1
xy
2
1
xz
2
1
yz
2
y 0
1
zy
2
где средняя деформация: 0
x y z
3
49,25 45 16,75 105
7 105
3
13
26
42,25
Д 13
52 19,5 105 ,
26
19,5 9,75
Д
2
И
9,355
2,878
5, 756
2
Д
9, 033 104
2,878
11,513
4,318
42, 25
13
26
13
52
19,5
,
26
5
19,5
10
9, 75
5, 756
4,318
.
2,159
8. Разложение заданного тензора напряжения на шаровой и девиатор.
33
Компоненты напряжённого состояния, действующие по граням элементарного параллелепипеда, выделенного в некоторой точке тела, вызывают изменение объёма и формы этого параллелепипеда. Относительное изменение
y z
объёма определяется зависимостью: 0 , где 0 x
- среднее
К
3
Е
гидростатическое напряжение, К
- модуль объёмной упругости,
3(1 2 )
y z
.
(50)
0 x
К
3К
Изменение формы параллелепипеда характеризуется наличием относительных деформаций x , y , z , xy , yz , zx , которые выражаются через компоненты напряжения по закону Гука (46).
Тензор напряжений Т можно представить в виде двух составляющих
тензоров, один из которых — шаровой Т0 — связан с изменением только объёма, а другой — D — вызывает изменение только формы:
(51)
T T0 D .
Эти тензоры имеют вид:
x xy xz
x 0
xy
xz
0 0 0
0
Т yx y yz ; T 0 0 0 ; D yx
y 0
yz .
0 0
zy
z 0
zy
z
zx
0
zx
100 45 50
В нашем случае 0
35 МПа, и следовательно,
3
100 20 40
35 0 0
65 20 40
20 45 30 0 35 0 2 80 30 .
40 30 50
0 0 35
40 30 15
T
T0
D
1) Объем изменяется 1) Объем изменяется
1) Объем не изменяется
y z 0
y z 0 0
3
x
;
0 0 ;
x
0;
3K
K
3K K
3K
K
2) по формулам (49):
2) по формулам (49): 2) по формулам (49):
1 2
x y z,
x y z
0,
x y z
E
xy 0; yz 0; zx 0,
xy yz zx 0,
" xy xy ; " yz yz ; "zx zx ,
следовательно, форма
элемента изменяется.
следовательно, форма
элемента не изменяется.
следовательно, форма элемента
изменяется.
Графическое разложение на шаровой и девиатор представлено на рисунке
19.
34
Z
Z
5035
30
40
40
45
15
30
=+
100
20
Z
35
x
20
20
x
35
y
40
65
80
30
y
40
20
x
30
y
Рисунок 19 - Графическое разложение тензора напряжений на шаровой тензор
и девиатор.
Примечание. Тензор деформаций также можно разложить на составляющие:
1
1
xz
x 0 2 xy
2
0 0 0
1
1
0
0
T T D ; где T 0 0 0 , D
xy y 0
yz , 0 x y z .
2
2
3
0 0
0
1
1
zx
zy z 0
2
2
9. Определение удельной потенциальной энергии деформации (полной, изменения объема, изменения формы).
Полная удельная потенциальная энергия деформации определяется по
формулам:
1
(52)
u ( 11 2 2 3 3 ) ,
2
1
или u
[12 22 32 2 (1 2 2 3 31 )].
2Е
Полную удельную потенциальную энергию u можно представить в виде
двух составляющих, одна из которой связана с изменением объёма u0, а другая
с изменением формы uФ в окрестности некоторой точки тела:
u u0 uФ .
(53)
Удельная потенциальная энергия изменения объёма и изменения формы
выражается зависимостями:
1 2
u0
( 1 2 3 )2 ;
(54)
6E
1 2
uФ
( 1 22 32 1 2 2 3 3 1 ).
(55)
3E
В нашем случае, из (52):
35
u
1
2
2
2
5 { 122, 22 42,57 ( 59, 79) 2 0,3 [ 122, 22 42,57 42, 57 ( 59, 79)
2210
2 Дж
( 59, 79) 122, 22 ]} 5, 779 10
.
3
см
Из (54):
u
o
из (55):
u
ф
(1 20,3)
62105
(1 0,3)
3210
5
(122, 22 42,57 59, 79) 3, 675 10
2
3
Дж
,
см3
[122, 22 42,57 ( 59, 79) 122, 22 42,57 42,57 ( 59, 79)
2
2
2
( 59, 79) 122, 22] 5, 41 10
2
Дж
см
3
;
u u u = 0,368 102 5,411 102 5,779 102
о
ф
Дж
.
см3
Сравниваем полученные значения для u:
5,779 10-2 5,779 102.
10. Определение расчётных напряжений по четырём классическим критериям
прочности и пластичности.
Первый критерий (прочности) — критерий наибольших нормальных напряжений:
Р 1 122,22 МПа.
(56)
Второй критерий (прочности) — критерий наибольших удлинений:
Р 1 ( 2 3 ) 122,22 0,3 (42,57 59,79) 127,39 МПа. (57)
Третий критерий (пластичности) — критерий наибольших касательных
напряжений:
Р 1 3 122,22 (59,79) 182,01 МПа.
(58)
Четвёртый критерий (пластичности) — энергетический:
РIV 12 22 32 1 2 2 3 3 1
122,222 42,57 2 59,79 122,22 42,57 42,57 ( 59,79) ( 59,79) 122,22
2
158,03 МПа.
Сравнение результатов определения Рi показывает, что при заданном
напряжённом состоянии наиболее неблагоприятные результаты получены при
применении критерия пластичности (энергетической теории).
Пример 2.
Балка-стенка толщиной 1 м нагружена на верхней кромке и частично
на нижней распределённой нагрузкой q и сверху сосредоточенной силой P .
Пролёт балки-стенки l , а высота её h .
36
Требуется определить напряжения x , y , xy в балке-стенке и построить
их эпюры в сечениях А-А и В-В; для сечения А-А построить эпюру x по формуле сопротивления материалов.
Рисунок 20 - Схема балки-стенки.
Решение:
1. Нанесём на балку стенку сетку (3x3) с шагом x 6 м, y 3 м . Затем
пронумеруем внутренние точки (узлы сетки), соблюдая при этом симметрию
системы (рисунок 21).
Рисунок 21 - Расположение узлов сетки.
2. Выбираем статически определимую раму с учётом симметрии. Для этого разрежем нижний ригель (рисунок 22).
37
Рисунок 22 - Модель соответствующей рамы.
Составляем уравнения равновесия:
a
a
M B 0, q a l d 2 P l d a P 2 RA l 2d 0,
a
a
q a l d P l d a P
2
2
RA
l 2d
45 6 (18 3 3) 140 (18 3 6) 140 3
410 кН/м;
18 6
аналогично определяем: RB= 410 кН/м.
Строим эпюры изгибающих моментов M и продольных сил N (рисунок 23).
M 14 RA d 410 3 1230 кН;
M 11 M 8 M 5 1230 кН;
a
a
6
M 6 RA q a 410 3 45 6 420 кН.
2
2
2
38
Рисунок 23 - Эпюры М и N для соответствующей рамы.
3. По формуле (20) находим функцию на контуре балки-стенки.
14 11 8 5 1230 кН; 6 420 кН; 15 0 .
4. По формуле (21) выразим функцию в законтурных точках через
внутриконтурные.
2 2 3 0 8 8 1230 кН,
3 2 3 0 9 9 ,
4 2 6 410 6 420 4920 4500 кН,
7 2 6 410 9 9 4920,
10 2 6 410 12 12 4920,
13 2 6 410 15 4920 кН, 17 2 3 0 11 11 1230 кН,
18 2 3 0 12 12 .
5. Запишем уравнения для каждой внутриконтурной точки:
6 2 8 69 4 1 6 9 12 8 2 5 6 12 11
3 28 15 27 0,
39
6
2
6
8 6 12 4 1 9 12 15 11 2 8 9 15 14
211 18 210 0,
y2 9
0,25,
x 2 36
8,3759 5 420 0,259 12 0,25 1230 0,5 1230 420 12 1230
где
9 0,0625 1230 0 0,0625 9 4920 0,
8,37512 5 9 0,2512 0 0,25 1230 0,5 1230 9 0 1230
420 0,0625 1230 12 0,0625 12 4920 0.
Приведём подобные слагаемые и получим:
8,18759 4,512 1966,875,
4,59 8,187512 343,125.
Решая систему, находим:
9 311,204 кН,
12 129,135 кН.
6. Напряжения в i-той точке получим по формулам (19).
Сечение А-А:
26 3 311,204 2 420 129,135
24,17 кПа,
x 6 9
9
9
29 6 129,135 2 311,204 420
8,14 кПа,
x 9 12
9
9
212 9 0 2 129,135 311,204
5,88 кПа,
x 12 15
9
9
215 12 129,135 2 0 129,135
28,7 кПа,
x 15 18
9
9
6 6 1230 2 420 420
45,83 кПа,
y 6 5 236
36
9 9 1230 2 311,204 311,204
42,81 кПа,
y 9 8 236
36
12 12 1230 2 129,135 129,135
37,75 кПа,
y 12 11 236
36
15 15 1230 2 0 0
34,17 кПа,
y 15 14 236
36
xy 6 2 372 9 8 1230 311,20472 311,204 1230 0 ,
xy 9 5 6 7212 11 1230 420 72129,135 1230 4,04 кПа,
40
8 9 15 14
1230 311,204 0 1230
4,32 кПа,
72
72
18 17 1230 129,135 129,135 1230
0.
xy 15 11 12 72
72
xy 12
Рисунок 24 - Эпюры напряжений x , y , xy в сечении А-А.
Сечение В-В:
28 5 1230 2 (1230) 1230
0,
x 8 11
9
9
29 6 129,135 2 311,204 420
8,14 кПа,
x 9 12
9
9
4608,796 2 1230 311,204
51,04 кПа,
y 8 7 2368 9
36
9 9 1230 2 311,204 311,204
42,81 кПа,
y 9 8 236
36
4790,865
0,
xy 8 4 6 7212 10 4500 420 129,135
72
xy 9 5 6 7212 11 1230 420 72129,135 1230 4,04 кПа,
1230 129,135
4,04 кПа,
xy 9 6 5 7211 12 420 1230 72
129,135
0.
xy 8 6 4 7210 12 420 4500 4790,865
72
41
Рисунок 25 - Эпюры напряжений x , y , xy в сечении В-В.
Построим эпюру X в сечении А-А методом сопротивления материалов.
Представим балку-стенку в виде обычной балки (рисунок 26).
Рисунок 26 - К расчету балки-стенки по балочной схеме
(метод сопротивления материалов).
MK
;
Wz1
M K RA 3 q 6 3 420 кНм;
x
Wz
a2
6
1 92
13,5 м3;
6
42
420
31,11 кПа.
13,5
Эпюра x показана на рисунке 24 пунктирной линией.
x
Пример 3.
Дана прямоугольная полоса-балка длиной l, высотой h и толщиной, равной 1 (рисунок 27). Начало координат О принято в середине торцового сечения. Главными осями поперечного сечения являются оси Oy и Oz. Продольная
ось Ox проходит посредине полосы-балки. Выражение для функции :
( x, y) 2 x4 9 x2 y 2 y 4 .
y
y
h
О
z
x
l
Рисунок 27. Схема полосы-балки.
Объемными силами пренебречь. Требуется:
1) проверить, можно ли предложенную функцию (x,y) принять для решения
плоской задачи теории упругости;
2) найти выражения для напряжений x, y, xy;
3) построить эпюры напряжений x, y, xy для одного сечения: либо перпендикулярного оси x, либо перпендикулярного оси y;
4) определить внешние силы (нормальные и касательные), приложенные ко
всем четырем граням полосы-балки, дать их изображение на рисунке полосы-балки и привести соответствующие эпюры.
Дано: l= 6 м, h= 1 м, x= 2 м, y= 0,3 м.
Решение:
1) Проверим, можно ли предложенную функцию (x,y) принять для решения
плоской задачи теории упругости. В этих целях используем бигармоническое
уравнение:
4
4
4
2
0.
x 4
x 2y 2 y 4
Находим производные:
43
2
3
4
2
2
8 x3 18 xy 2 ,
24
x
18
y
,
48
x
,
48,
x
x 2
x3
x 4
2
3
4
2
2
2
3
18 x 12 y ,
24 y ,
24,
18 x y 4 y ,
y 2
y 3
y 4
y
3
4
36 y,
36.
x 2y
x 2y 2
Подставляем найденные производные в бигармоническое уравнение:
48 36 2 24 0,
0 0.
Следовательно, заданное (x,y) тождественно удовлетворяет бигармоническому уравнению плоской задачи теории упругости и может быть принято
для решения этой задачи.
2) Находим выражения для напряжений:
2
2
2
2
x 2 18 x 12 y ,
y 2 24 x 2 18 y 2 ,
y
x
2
2
36 xy,
xy
36 xy.
xy
xy
Выполняем проверку выполнения уравнений равновесия:
x xy
x y 0,
yx y 0.
x
y
Для этого находим соответствующие производные:
xy
y
xy
x
36 x,
36 y,
36 x,
36 y,
y
y
x
x
36 x 36 x 0,
36 y 36 y 0.
3) Строим эпюры напряжений в сечении x= 1 м. В данном случае:
x 18 12 y 2 ,
xy 36 y.
y 24 18 y 2 ,
h
По указанным выражениям для напряжений, изменяя y от 0,5 м до
2
h
0,5м, строим их эпюры.
2
Таблица 2. Расчет значений напряжений в сечении x= 1 м.
-0,5
0
0,5
-69
-72
-69
x
31,5
96
91,5
y
-36
0
36
xy
44
Ýï þðà
x
y
xy
Рисунок 28 – Эпюры напряжений в сечении x= 1 м.
4) Определяем внешние силы (нормальные и касательные), приложенные ко
всем четырем граням полосы-балки. Для этого воспользуемся условиями на
поверхности тела (условиями на контуре или статическими граничными условиями):
px x cos x, xy cos y, ,
p y yx cos x, y cos y, ,
где px, py - проекции на оси Оx и Oy внешних сил, действующих на гранях полосы-балки; - нормаль к грани; cos(x,), cos(y,) - направляющие косинусы
нормали .
Верхняя грань: y
h
0,5 м;
2
x 18 x 2 12 0,52 18 x 2 3,
xy 36 x 0,5 18 x.
l=cos(x,)=cos(x,y)=0,
px x 0 xy 1 xy 18 x,
y 24 x2 18 0,52 24 x2 4,5,
m=cos(y,)=cos(y,y)=1,
py xy 0 y 1 y 24 x2 4,5.
px=x0+xy1=xy=18x,
py=xy0+y1=y= 24 x2 4,5.
Для сил, нормальных py и касательных px строим их эпюры, изменяя x от 0 до
l= 6 м.
Таблица 3. Расчет нормальных и касательных сил для верхней грани.
0
3
6
0
54
108
px
-4,5
211,5
859,5
py
h
2
Нижняя грань: y -0,5 м;
x 18 x 2 12 0,5 18 x 2 3,
xy 36 x 0,5 18 x,
2
y 24 x 2 18 0,5 24 x 2 4,5,
2
45
l=cos(x,)=cos(x,-y)=0,
px x 0 xy 1 xy 18 x,
m=cos(y,)=cos(y,y)=-1,
py xy 0 y 1 y 24 x2 4,5.
Для сил, нормальных py и касательных px строим их эпюры, изменяя x от 0 до
l=6 м.
Таблица 4. Расчет нормальных и касательных сил для нижней грани.
0
3
6
0
54
108
px
4,5
-211,5
-859,5
py
Левая грань: x 0 ;
x 12 y 2 ,
xy 0,
y 18 y 2 ,
l=cos(x,)=cos(x,-x)=-1;
px x 1 xy 0 x 12 y 2 ,
m=cos(y,)=cos(y,-x)=0;
p y xy 1 y 0 xy 0.
Для сил, нормальных px и касательных py строим их эпюры, изменяя y от
h
h
-0,5 м до 0,5 м.
2
2
Таблица 5. Расчет нормальных и касательных сил для левой грани.
-0,5
0
0,5
-3
0
3
px
0
0
0
py
Правая грань: x l 6 м;
x 18 62 12 y 2 648 12 y 2 ,
y 24 62 18 y 2 864 18 y 2 ,
xy 36 6 y 216 y,
l=cos(x,)=cos(x,x)=1;
px x 1 xy 0 x 648 12 y 2 ,
m=cos(y,)=cos(y,x)=0;
p y xy 1 y 0 xy 216 y.
Для сил, нормальных px и касательных py строим их эпюры, изменяя y от
h
h
-0,5 м до 0,5 м.
2
2
Таблица 6. Расчет нормальных и касательных сил для правой грани.
-0,5
0
0,5
-645
-648
-645
px
-108
0
108
py
Эпюры сил, действующих на все четыре грани, приведены на рисунке.
46
Ýï þðà
Px
Ýï þðà
Py
Ýï þðà
Px
Ýï þðà Ýï þðà
Py
Py
Ýï þðà
Py
Ýï þðà
Px
Рисунок 29 – Эпюры нормальных и касательных сил
Пример 4.
Дана прямоугольная изгибаемая пластина (рисунок 30). Требуется:
47
1) установить граничные условия, которым удовлетворяет функция прогибов
w(x, y);
2) проверить, удовлетворяет ли функция w(x, y) уравнению Софи Жермен
q
22w , и если это не так, то использовать уравнение Бубнова-Галеркина:
D
q
2 2
( w) wdS wdS . Из этих уравнений определить постоянную С;
S
SD
3) по формулам для Mx, Myx, Mxy, Qx, My, Qy составить их выражения;
4) построить эпюры изгибающих моментов M x в сечении x=0 b M y в сечении
y=0.
Дано:
y
2b
x
0
2a
3 y
,
2a
2b
x
3 y
w C cos
cos
,
2a
2b
а=3м,
v=0,3,
b=2м,
Е=2105 МПа,
q0=2 МПа, []=200 МПа.
q q0 cos
x
cos
Рисунок 30 - Расчетная схема пластинки.
Решение:
1. Установим, каким граничным условиям удовлетворяет функция
прогибов w(x, y).
При x=a, w=0,
y=b, w=0.
Следовательно, пластинка оперта по всем четырем краям. Определим тип
опирания. Углы поворота:
3
x
3 y
w
x
3 y w
C sin
cos
,
C
cos
sin
,
x
2a
2a
2b
y
2b
2a
2b
w
при x=a,
0,
x
w
y=b,
0.
y
Значит, пластинка не защемлена. Проверим шарнирное опирание:
2w
2w
2w
2 w
M x D
=0, M y D
=0,
2
2
2
2
y
x
x
y
48
2 x
3 y
C cos cos
;
2
2
a
2
a
2
в
x
2
x 3 y
2w
3
C cos cos
;
2
2
в
2
a
2
в
y
2w 2w
0,
тогда при x=a,
2
2
x
y
2w 2w
0.
y=b,
y2
x2
Итак, пластинка шарнирно оперта по всем четырем краям (рисунок 31).
2w
y
x
Рисунок 31 - Схема закрепления пластинки.
2. Проверим, удовлетворяется ли уравнение Софи Жермен. Для этого вычислим производные:
3 y
4w 4 x
C cos cos
;
4
2
a
2
a
2
в
x
2
2
x
3 y
4w
3
C cos cos
;
2
2
2
a
2
в
2
a
2
в
x y
3 y
4w 3 4 x
C cos cos
.
4
2
в
2
a
2
в
y
Подставим значения производных и q(x, y) в бигармоническое уравнение:
2
1 2 3 2
x 3 y
x 3 y
CD 4 cos cos
q0cos cos
;
2a
2в
2a
2в
2a 2в
видим, что уравнение выполняется при соответствующем выражении для С.
Определяем постоянную С:
49
q0
C
.
2
2
2
1 3
D 4
2a 2в
3. Составим выражения для Mx, My, Mxy, Qx, Qy.
3w 3 x
3 y
C sin cos
;
Вычислим производные:
3
2
a
2
a
2
в
x
3 w 3 3 x 3 y
C cos sin
;
3
2
в
2
a
2
в
y
2w 3 x 3 y
C sin sin
;
x y 2a 2в 2a
2в
3w
3 2 x 3 y
C sin cos
;
2
2
a
2
в
2
a
2
в
x y
2
x 3 y
3w
3
C cos sin
.
2a
2в
x 2y 2a 2в
Тогда с учетом выражения С, получим:
1
9
4q0 ( a 2 в 2 )
x
3 y
Mx 2
cos
cos
;
2a
2в
1 9 2
2 2
a в
9 1
4q0 в 2 a 2
x
3y
My 2
cos cos
;
2a
2в
1 9
a 2 в2
M xy
12q0 (1 )
aв 2 12 92
a в
sin
2
x
2a
sin
3y
;
2в
50
Q
x
2q 13 92
0 a
ab
2
12 92
a
b
sin
Q
y
2q 27
92
3
0 b
a b
2
12 92
a
b
cos
4. Построим эпюры Mx в сечении x=0
x
2a
x
2a
cos
3 y
;
2b
sin
3 y
.
2b
и эпюры My, Mxy, Qy в сечении
y=0.
при
при
при
при
при
при
1
9
4q 2 в2
3 y
3 y
cos
114 cos
( kH )
x=0, M x 0 a
2
2
2
в
2
в
1 9
a 2 в2
Myx=0;
Qx=0;
y=b: Mx=0,1141060=0;
y=b/2: Mx=0,114106(-0,707)= - 81 кH;
y=0:
Mx=0,1141061= 114 кH;
9
1
2
2
4q0 в
x
x
a
cos 332cos ( kH )
y=0, M y
2a
2a
2 1 9 2
2 2
a в
Mxy=0;
Qy=0;
x=a:
My=3320=0;
x=a/2: My=332(-1)= - 332 кH;
x=0:
My=3321= 332 кH.
По полученным значениям строим эпюры Mx, My (рисунок 32).
51
Эпюра Мх, кН
b
Эпюра Мy, кН
y
81
114
b
81
а
х
b
y
332
х
b
а
332
332
а
а
а)
б)
Рисунок 32. Эпюры изгибающих моментов.
Пример 5.
Кольцевая пластина (рисунок 33) жестко защемлена по наружному контуру
и нагружена радиальными изгибающими моментами m , равномерно распределенными по внутреннему контуру.
Рисунок 33 – Схема кольцевой пластины.
Требуется:
1. Проверить граничные условия.
2. Определить постоянную С.
3. Составить выражения для внутренних сил.
4. В диаметральном сечении построить эпюры M r , M .
r a2 r 2
W C2 n
, а=8 м, b =4 м, 0,3 .
a
a2
Решение:
1. Проверка граничных условий. Прогиб и угол поворота в радиальном
направлении при r=a должны быть равны нулю:
52
dw
0.
dr
a a2 a2
w(r ) C 2 n
0;
2
a
a
a 1 2r
1 r
r C 2 2 2C 2 ;
r a a
r a
при r a, w 0 , r
1 a
0.
2
a a
Граничные условия выполняются.
2. Определение постоянной С.
Используем условие: при r b, M r m .
Находим производные:
d 2w
1 1
2C 2 2 ;
2
dr
a
r
dw
1 r
1 1
2C 2 2C 2 2 ;
r dr
rr a
a
r
a 2 (1 ) r 2 (1 )
1 1
M r 2CD 2 2 2 2 2CD
.
a
r
a
a 2r 2
r
a 2 (1 ) b2 (1 )
2CD
m;
a 2b2
кн м 4
2 2
м м
ma b
C
м
.
2 D a 2 (1 ) b 2 (1 ) кн м м 2
2. Находим выражения для M r , M :
mb 2
a2
Mr 2
(1 ) (1 ) 2 ,
r
a (1 ) b 2 (1 )
r (a) 2C
1 dw
1 1
2C 2 2 ;
r dr
a
r
d 2w
1 1
2 2C 2 2 ;
dr
a
r
mb 2
a2
1 1
M 2CD 2 2 2 2 2
(1
)
(
1
)
.
a
r
a
r 2
a (1 ) b 2 (1 )
r
3. Строим эпюры M r , M (рисунок 30).
Вычислим:
53
b2
42
0,244,
a 2 (1 ) b2 (1 ) 82 (1 0,3) 42 (1 0,3)
44,8
M r 0,244m 1,3 2 ;
r
44,8
M 0,244m 1,3 2 .
r
Находим:
при r 4 м, M r m ; M =-0,366 m ;
при r = 6 м, M r 0,621m ; M = 0,014 m ;
при r = 8 м, M r 0,488m ; M = 0,146 m .
Mr
m
m
+
m
+
m
M0
m
m
m
m
m
m
Рисунок Рис.
34 -6.2
Эпюры моментов.
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа включает 2 задачи. Студенты с последней четной цифрой номера группы решают задачи 1, 2, нечетной цифрой – 3 и 4.
ЗАДАЧА 1. ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО
СОСТОЯНИЯ В ТОЧКЕ УПРУГОГО ТЕЛА
Заданы компоненты напряжения на гранях элемента, вырезанного в некоторой точке
загруженного тела. Тело изотропно, материал
подчиняется закону Гука. Модуль продольной
упругости Е и коэффициент Пуассона определяются по таблице 2.
Рисунок 35.
54
Требуется:
1) Нанести исходные компоненты тензора напряжений на гранях элементарного параллелепипеда, выделенного в окрестности рассматриваемой точки.
2) Определить величину и направление главных напряжений.
3) Вычислить компоненты тензора деформаций в заданных осях, построить
тензор деформаций.
Числовые данные для выполнения задачи следует выбирать из таблицы 2 согласно пяти последним цифрам шифра и первым пяти буквам
русского алфавита.
Например, записав шифр и под каждой цифрой его буквы:
шифр 1 0 1 7 2 3
буква а б в г д,
выбирают из указанной таблицы число, которое находится на пересечении соответствующих строки и столбца. Причем, вначале берется буква, а затем по
ней определяется цифра.
ПРИМЕР. Шифр 101723. В таблице 7 по горизонтали в последней строке
первая буква "а". На пересечении этого столбца со строчкой, соответствующей
цифре шифра, т.е. цифре 0, находится x 60 МПа. Затем по следующей букве "б" и соответствующей цифре шифра 1, пересечении столбца "б" и строки
"1", получаем величину " y " и т.д.
Таблица 7. Числовые данные к задаче 1
x,
z,
y,
xy ,
№
стро МПа МПа
МПа МПа
-ки
1
30
-40
60
20
2
-80
20
-50
30
3
50
-20
40
-10
4
-20
30
-40
10
5
40
-50
20
-20
6
20
-10
-30
50
7
-40
50
50
-30
8
-90
80
-60
40
9
-30
-70
70
-40
0
-60
-50
-80
-50
а
б
в
г
yz ,
E,
ГПа
МПа
zx ,
МПа
-10
40
10
-60
80
-30
10
-70
-20
-40
д
30
-10
20
10
-60
70
-90
-40
-50
-30
а
220
150
120
85
100
70
60
70
80
110
в
0,3
0,25
0,22
0,32
0,35
0,33
0,25
0,23
0,27
0,36
г
ЗАДАЧА 2. РАСЧЕТ БАЛКИ-СТЕНКТ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
Для заданной схемы балки-стенки требуется:
1) определить значения функции напряжений во всех узлах предварительно
нанесенной сетки (33) методом конечных разностей;
55
2) подсчитать напряжения x , y , xy в узловых точках сетки и построить
эпюры этих напряжений в одном из вертикальных сечений;
3) сравнить полученное решение с решением сопротивления материалов и
выполнить анализ результатов сравнения.
Схема закрепления балки-стенки приведена на рисунке 36. Cхемы
загружения балки-стенки (рисунок 37) следует принимать по двум последним цифрам шифра. Во всех вариантах принять P 0 .
Числовые данные для выполнения задачи следует выбирать из таблицы 8 согласно пяти последним цифрам шифра и первым пяти буквам
русского алфавита (пояснение в условии задачи 1).
Таблица 8. Числовые данные к задаче 2.
l
h
a
b
№
(м)
(м)
(м)
стро- (м)
ки
1
9
6
0
0
2
12
6
l/6
l/2
3
12
9
l/3
l/3
4
15
9
l/2
l/6
5
15
12
0
l/6
6
18
9
l/6
l/3
7
18
12
l/3
l/2
8
18
15
l/2
0
9
21
12
0
0
0
21
18
l/3
l/3
в
д
в
d
(м)
q
(Кн/м2)
P
(Кн/м)
0
1
2
3
4
4
3
2
1
0
10
50
25
45
65
40
35
50
40
25
80
160
100
140
100
120
110
80
120
70
д
г
Рисунок 36 - Схема закрепления балки-стенки.
56
d
d
d
d
Схема загружения балки - стенки
q
P
P
*
b
*
b
q
P
P
1
h/2
P
q
*
4
a
a
a
P
*
b
h/2
q
P
b
b
8
l/2
a
a
10
P*
9
h/2
a
a
q
P
q
b
b
q
q
P
a
q
P
l/2
a
P
b
a
h/2
q
7
*
b
q
P
q
6
a
q
P
P*
5
a
P
P
b
b
l/2
*
3
h/2
P
h/2
b
q
P
2
h/2
q
P*
b
*
P
q
P
q
b
P*
L/2
P
*
11
12
Рисунок 37 - Схемы загружения балки-стенки.
57
Продолжение рисунка 37
P
b
P
P
b
P
P
b
b
*
q
P
P*
q
b
b
*
P
h/2
P
h/2
13
b
P
q
b
14
15
P
l/2
q
P
b
P*
b
q q
P*
16
h/2
P
h/2
q
P*
a
17
a
18
h/2
q
P
q
l/2
P
q
q
P*
P*
a
19
q
a
PP
q
P*
l/2
20
h/2
P
q
21
h/2
P
q
P
q
P*
b
b
P*
b
b
b
b
P*
22
h/2
23
h/2
24
q
q
l/2
P
q
P
P*
b
P*
h/2
a
25
P
a
h/2
a
26
a
P
P
b
P
b
b
h/2
q
P
q
P
b
P*
28
27
q
P
P*
h/2
l/2
b
P*
2P
b
P
b
P*
l/2
29
a
q
a
P
a
q
30
l/2
a
58
ЗАДАЧА 3. РАСЧЕТ ПОЛОСЫ-БАЛКИ.
Дана прямоугольная полоса-балка длиной l, высотой h и толщиной, равной 1. Начало координат О принято в середине торцового сечения. Главными
осями поперечного сечения являются оси Oy и Oz. Продольная ось Ox проходит посредине полосы-балки. Объемными силами пренебречь.
y
y
h
О
z
x
l
Рисунок 38 – Схема полосы - балки.
Требуется:
1) проверить, можно ли предложенную функцию (x,y) принять для решения
плоской задачи теории упругости;
2) найти выражения для напряжений x, y, xy;
3) построить эпюры напряжений x, y, xy для одного сечения: либо перпендикулярного оси x, либо перпендикулярного оси y;
4) определить внешние силы (нормальные и касательные), приложенные ко
всем четырем граням полосы-балки, дать их изображение на рисунке полосы-балки и привести соответствующие эпюры.
Числовые данные для решения задачи следует выбирать из таблицы 4
согласно шести последним цифрам шифра и первым шести буквам русского алфавита (пояснение приведено в условии к задаче 1).
Таблица 9. Исходные данные к расчету полосы-балки
a
b
№
Функция напряжений ( xy )
строки
1
1
1
a( x 4 y 4 ) bx3 y xy 3
2
2
1
ax( x 2 y 2 ) bx 2 y xy
3
4
5
ay( x 2 y 2 ) bxy 2 xy
x4
axy3 b( x 2 y 2 )
3
3
2
2
ax bx y xy xy
l
y
x
h
м
5
1
1
0,2
6
1
2
0,3
2
1
5
2
2
0,4
1
2
6
1
2
0,3
1
2
6
2
2
0,5
59
6
a( x 4 y 4 ) by 2 by 2 ( x2
7
8
2
2
4
2
1
0,5
a( y 4 x 4 ) bxy 3 x 2 y)
2
1
4
2
1
0,5
a 4
1
( x y 4 ) xy (bx 2 y 2 )
12
3
1
1
1
x3 y bx 2 y 2 by 4
3
2
6
1
1
1
axy 3 bx 2 y 2 bx 4
3
2
6
е
2
1
6
1
3
0,3
1
2
5
1
2
0,2
2
1
5
2
2
0,4
д
е
г
д
е
в
y2
)
3
9
0
ЗАДАЧА 4. РАСЧЕТ ТОНКИХ ПЛАСТИН.
Номер варианта выбирается в соответствии с суммой 3-х последних
цифр шифра.
Варианты 1-15. Расчет прямоугольной пластины.
Дана прямоугольная изгибаемая пластина (рисунок 39).
1.
2.
y
0
x
b
b
0
x
b
a
y
a
a
Рисунок 39. Схема пластины
Требуется:
1) установить граничные условия, которым удовлетворяет функция прогибов
w(x, y);
2) проверить, удовлетворяет ли функция w(x, y) уравнению Софи Жермен
q
22w , и если это не так, то использовать уравнение Бубнова-Галеркина:
D
q
2 2
( w) wdS wdS . Из этих уравнений определить постоянную С и выS
SD
числить максимальный прогиб Wmax;
3) по формулам для M x , M y , M xy ,Qx ,Q y составить их выражения;
4) построить эпюры внутренних сил в одном из сечений: сечение x - эпюры
M x ,Qx , M xy ; сечение y - эпюры M y ,Qy , M yx .
60
Функции для прогиба и нагрузки взять из таблицы 10, а числовые
значения – из таблицы 11. Числовые данные по таблице 11 выбираются
согласно шести последним цифрам шифра и первым шести буквам русского алфавита (см. пример в условии задачи 1).
Таблица 10. Числовые данные к расчету прямоугольных пластин
Сумма трех
Вид пластины по рисунку 39. Выражения для нагрузки
последних
q(x, y) и прогиба W( x, y) .D, С и q 0 - постоянные величины
цифр шифра
0
Рисунок 39 а
q const ; W C ( x a)2 ( y b)2
1
Рисунок 39 а
q const ; W Cxy( x a)( y b)
2
Рисунок 39 а
x y
x y
q q0 sin sin
;W C sin sin
a
b
a
b
3
Рисунок 39 а
x 2 y
x 2 y
q q0 sin sin
;W C sin sin
a
b
a
b
4
Рисунок 39 а
2 x y
2 x y
q q0 sin
sin
;W C sin
sin
a
b
a
b
5
Рисунок 39 b
x
y
x
y
q q0 sin
cos
;W C sin
cos
a
2b
a
2b
6
Рисунок 39 b
x y
x y
q q0 cos sin
;W C cos sin
2a
b
2a
b
7
Рисунок 39 b
2 x
y
2 x
y
q q0 sin
cos
;W C sin
cos
a
2b
a
2b
8
Рисунок 39 b
x 2 y
x 2 y
q q0 cos sin
;W C cos sin
2a
b
2a
b
9
Рисунок 39 b
q const ; W C ( x 2 a 2 )( y b)2
10
Рисунок 39 b
q const ; W C ( x a)2 ( y 2 b2 )
11
Рисунок 39 b
q const ; W C ( x 2 a 2 )( y 2 b2 )
61
12
13
14
15
Рисунок 39 b
x
y
x
y
q q0 cos cos
;W C cos cos
2a
2b
2a
2b
Рисунок 39 b
3 x
3 y
3 x
3 y
q q0 cos
cos
;W C cos
cos
2a
2b
2a
2b
Рисунок 39 b
3 x
y
3 x
y
q q0 cos
cos
;W C cos
cos
2a
2b
2a
2b
Рисунок 39 b
x
3 y
x
3 y
q q0 cos cos
;W C cos cos
2a
2b
2a
2b
Таблица 11. Числовые данные к задаче 4.
№
м
a
b
h
1
4
3
0,1
2
3
3
0,1
3
3
3
0,1
4
4
4
0,2
5
5
3
0,1
6
3
5
0,1
7
3
3
0,2
8
5
5
0,2
9
5
4
0,2
0
4
5
0,2
д
е
б
x
3
2
1
2
3
1
2
2
3
2
г
y
2
2
1
3
1
3
2
2
1
3
д
0,35
0,30
0,25
0,25
0,30
0,30
0,35
0,35
0,30
0,30
е
Варианты 16-27. Расчет круглой или кольцевой пластины.
Дана круглая сплошная или кольцевая пластина. Для данной схемы закрепления требуется:
1. Проверить граничные условия.
2. Определить постоянную С.
3. Составить выражения для внутренних сил.
4. В диаметральном сечении построить эпюры M r , M .
Функцию прогибов взять из таблицы 12, а числовые значения – из таблицы
13.
62
а)
с)
b)
a
a
2a
a
2a
m
2a
2a
g)
a
m
a
2a
f)
e)
d)
a
a
m
m
2a
m
m
2a
Рисунок 40Рис.
- Схемы
6.1 круглых и кольцевых пластин.
Таблица 12. Выражения для нагрузки и прогибов.
Сумма трех поВид пластины по рисунку 40.
следних цифр
Выражения для нагрузки и прогиба W(r).
шифра
D и С постоянные величины.
5 2 2
a r
Рисунок 40.а; q const ; W C (a 2 r 2 )
16
1
2
2 2
Рисунок 40.b; q const ; W C (a r )
17
r
3 2 2
( a r ) 2r 2 n
Рисунок 40.c; W C
18
a
1
19
20
21
22
r a2 r 2
Рисунок 40.d; W C r 2 n
a
2
a 2 r 2 2(1 ) b 2 r
n
Рисунок 40.e; W C
2
2
a
1
a
a
a 2 r 2 2(1 ) r
n
Рисунок 40.f; W C
2
a
1
a
r a2 r 2
Рисунок 40.g; W C 2 n
a
a2
63
25
q 4
r
64 D
q 4
Рисунок 40.b; q const ; W C3 C4r 2
r
64 D
Рисунок 40.d; W C1 nr C2r 2 nr C3 C4r 2
26
Рисунок 40.e; W C1 nr C2r 2 nr C3 C4r 2
27
Рисунок 40.g; W C1 nr C2r 2 nr C3 C4r 2
Рисунок 40.а; q const ; W C3 C4r 2
23
24
Примечания:
1. Радиальные моменты m , равномерно распределены по внутреннему или наружному
контуру.
2. Нагрузка q равномерно распределена по площади пластины.
3. В вариантах 18 и 19 постоянную С можно определить из равенства:
3 W 1 2 W 1 W
F .
D 3
2
2
r
r
r
2 а
r
r
4. В варианте 20 постоянную С можно определить из равенства: при r a , M r m ; в вариантах 21, 22 из условия: при r b, M r m .
5. В варианте 23 постоянные С3, С4 находим из условий: при r a , W 0, M r 0 ; в варианте 24: при r a , W 0, dW dr 0 .
6. Постоянные С1, С2, С3, С4 определяются из условий:
вариант 25: при r b, Q r 0 ; M r 0 ;
при r a, W 0 ; M r m ;
вариант 26: при ; M r m ;
при r a, W 0 ; M r 0 ;
вариант 27: при r b, Q r 0 ; M r 0 ;
при r a, W 0 ; dW dr 0 .
Таблица 13. Числовые данные к расчету круглой или кольцевой пластины
м
№ строки
а
b
h
1
6
4
0,1 0,25
2
5
3
0,1 0,27
3
4
2
0,2
0,4
4
5
3
0,2
0,3
5
5
3
0,2 0,33
6
6
4
0,1 0,29
7
6
3
0,1 0,35
8
5
3
0,2
0,4
9
5
3
0,1 0,36
0
6
3
0,2 0,32
д
е
д
г
64
ЛИТЕРАТУРА
1. Безухов Н.И. Основы теории упругости, пластичности и ползучести. - М.:
Высшая школа, 1968.
2. Тимошенко С.П., Гудьер Дж. Теория упругости. - М.: Высшая школа, 1979.
3. Киселев В.А. Плоская задача теории упругости. - М.: Высшая школа, 1976.
4. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. М.: Высшая школа, 1990.
5. Рочняк О.А., Фёдоров В.Г., Хвисевич В.М. Основы теории упругости.-Брест:
Изд-во БрГТУ, 2001.
6. Рекач В.Г. Руководство к решению задач прикладной теории упругости. –
М., 1984.
65
УЧЕБНОЕ ИЗДАНИЕ
Составители:
Веремейчик Андрей Иванович
Хвисевич Виталий Михайлович
ТЕОРИЯ УПРУГОСТИ И ПЛАСТИЧНОСТИ
методические указания и задания
к выполнению контрольной работы
для студентов специальности 1- 70 02 01 – “Промышленное и гражданское
строительство” факультета инновационной деятельности и финансов
Ответственный за выпуск: Веремейчик А.И.
Редактор: Строкач Т.В.
Технический редактор: Никитчик А.Д.
__________________________________________________________
Подписано к печати __.__.200_ г. Бумага писч. № 1. Гарнитура Times
New Roman. Усл. печ. л. __.___. Уч. изд. л. __.__.
Заказ № ____.Тираж _____ экз. Отпечатано на _______________
Брестского государственного технического университета.
224017, г. Брест, ул. Московская, 267.
66