Документ 4763889

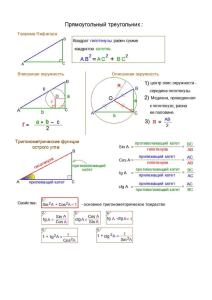
Простейший из многоугольников –
треугольник – играет в геометрии
особую роль.
Без преувеличения можно сказать,
что вся (или почти вся) геометрия
со времён «Начал» Евклида
покоится на «трёх китах» - трёх
признаках равенства
треугольников.
Исторический материал
Любой геометрический
материал возникает из
потребностей окружающей
жизни. Доказательство
признаков равенства
треугольников приписывают
древнегреческому ученому
Фалесу Милетскому (жившему
ок.625-547г.г. до н.э.). Теорему
о равенстве треугольников по
стороне и прилежащим к ней
двум углам он использовал для
определения расстояния от
берега до морских кораблей.

В древнем искусстве очень широко распространяются
изображения равностороннего треугольника .
Первобытные люди штамповали треугольники на разных
изделиях.

Вожди племен северо-американских
индейцев носили на груди символ власти: равносторонний
треугольник с точкой в центре,
в Африке женщины также украшают себя большими
пластинами из равносторонних треугольников.

Равносторонние треугольники рисовали на изображениях
священных животных.
Для составления красивых паркетов часто использовали треугольники .
Лишь на рубеже XIX – XX веков
математики научились строить
геометрию на основе более
фундаментального и общего,
чем равенство треугольников,
понятия геометрического
преобразования.
За несколько тысячелетий
геометры столь подробно
изучили треугольник, что
иногда говорят о
«геометрии треугольника»
как о самостоятельном разделе
элементарной геометрии.
Вопрос 1. Определение
треугольника
В
А
С
Вопрос 2. Определение
остроугольного треугольника
В
А
С
Вопрос 3. Определение
прямоугольного треугольника
А
С
В
Вопрос 4. Определение
тупоугольного треугольника
О
Н
Т
Вопрос 5. Определение
равностороннего треугольника
В
А
С
Вопрос 6. Определение
равнобедренного
треугольника
О
М
С
Вопрос 7. Медиана треугольника
(определение)
В
С
А
М
Вопрос 8. Медианы треугольника
(замечательное свойство)
В
К
Р
А
М
С
Вопрос 9. Свойство медианы
равнобедренного треугольника
В
С
А
М
Вопрос 10. Биссектриса
треугольника (определение)
В
О
А
С
Вопрос 11. Биссектрисы
треугольника ( свойство)
В
Н
А
К
М
С
Вопрос 12. Биссектриса
равнобедренного треугольника
В
С
А
К
Вопрос 13. Высота
треугольника
В
АН
Н
А
С
ВС
Вопрос 14. Высоты
треугольника (замечательное
В
свойство)
О
К
А
М
О
К
С
Н
Н
В
С
А
М
Вопрос 15. Свойство высоты
равнобедренного
треугольника
В
А
С
Н
Вопрос 16. Свойство углов при
основании
равнобедренного треугольника
В
К
С
Вопрос 17. Равные треугольники

Вопрос 18. Первый признак равенства
треугольников
С
К
В
Р
М
А
(По двум сторонам и углу между
ними )

Вопрос 19. Второй признак равенства
треугольников
М
В
С
Р
А
К
( по стороне и двум прилежащим к ней углам )

Вопрос 20. Третий признак
равенства треугольников
К
В
С
Т
М
(По трём сторонам)
Вопрос 21. Равные треугольники
В
С
О
А
D
AOB=
COD
(по стороне и двум углам)
Вопрос 22. Равные треугольники
E
C
DEC=
DKC
(по двум
сторонам и углу)
K
D
Вопрос 23. Равные треугольники
ADB=
ADC
(по двум сторонам и углу)
В
А
1
D
2
С
Вопрос 24. Равные треугольники
E
C
K
D
DEC = DKC
(по трем
сторонам)
Вопрос 25. Равные треугольники
Е
В
А
С
D
АСЕ = АВD
(по стороне и двум углам)
Вопрос 26. Равные треугольники
CAF = CBF
(по трем сторонам)
А
С
F
В
Вопрос 27. Равные треугольники
CAE= DBE
(по двум сторонам и углу)
Е
С
D
А
О
В
Вопрос 28.
СОСЧИТАЙ
ТРЕУГОЛЬНИКИ
Задача Фалеса
Требовалось определить
расстояние от берега до корабля,
находящегося недалеко в море.
Для этого допустим, что корабль
находится в точке A, а наблюдатель в
точке B.
Строим на суше перпендикулярно
отрезку AB отрезок BC произвольной
длины, находим его середину (точку D).
Строим перпендикулярно CB отрезок
CE так, чтобы точки E, D и A зрительно
лежали на одной прямой.
Тогда AB = CE. Докажите .
А
С
D
B
Е
Задачи с практическим
содержанием
Задача 1
Листок календаря частично
закрыт предыдущим листком.
Определите размеры
листка по данным,
указанным на рисунке.
C
B
3
E
K
1
A
4
D
Н
F
КА = 1, СЕ = 3, ED = 4.
Указания к решению задачи
Докажите равенство
∆ КВС и ∆ DEС.
3
B
C
3
E
4
4
K
1
A
D
Н
F
Решение задачи
1. Рассмотрим ∆ КВС и ∆ DEС.
1) ВС=СЕ (сторона прямоугольника).
2) КС=СD (сторона прямоугольника)
4
3)
ВСК =
DСЕ, т.к.
ВСК = 90° - х
K
DСЕ = 90° -х
1
Значит, ∆ КВС = ∆ DEС (по двум
A
сторонам и углу).
2. АВ=АК+КВ , АВ= 1+4=5
ВС=СЕ=3
Ответ. АВ=5, ВС=3.
3
B
C
3
х
E
4
D
Н
F
Задачи с практическим
содержанием
Задача 2
Лежащий на полу ковер
прямоугольной формы,
сложили по диагонали.
Выполнив измерения,
указанные на рисунке.
Саша быстро восстановил
4
размеры ковра. Как он это сделал?
5
3
Указания к решению задачи
C
B
Докажите равенство
∆ AFE и ∆ CDE.
4
5
5
A
A
E
4
3
F
3
D
D
Pешениe задачи
1. Рассмотрим ∆ АFЕ и ∆ СDE.
1) АF=СD (стороны прямоугольника).
2)
АFЕ= ЕDС = 90° ;
B
3)
FАЕ=
DСЕ, т.к.
FАЕ= 90°- х
DСЕ= 90°-х (сумма углов
треугольника 180°).
A
A
Значит, ∆ АFЕ = ∆ СDE
4
(по стороне и двум углам).
2. АВ=CD=АF=4,
ВС=AD=AЕ+ED, AD=5+3=8,
Ответ. АВ=4, ВС=8.
C
4
5
5
х E
3
F
х
3
D
D
В
19 марта 2010 года Шуховской башне
на Шаболовке исполнилось 88 лет.
Высоковольтные линии электропередачи.
Треугольники делают конструкции надежными.
Треугольники в конструкции мостов.
Начиная игру в бильярд, необходимо расположить шары в виде
треугольника. Для этого используют специальную треугольную рамку.
Расстановка кеглей в игре Боулинг тоже в виде равностороннего
треугольника.
Треуго́ льник — ударный музыкальный
инструмент в виде металлического прута ,
изогнутого в форме треугольника. Один из
углов оставлен открытым (концы прута
почти касаются).
Треуго́ льник — созвездие северного полушария неба, содержит
25 звезд, видимых невооружённым глазом.
Бермудский треугольник — район в Атлантическом океане, в котором
происходят якобы таинственные исчезновения морских и воздушных судов.
Район ограничен линиями от Флориды к Бермудским островам, далее к
Пуэрто-Рико и назад к Флориде через Багамы.
Бермудские
острова
Флорида
Пуэрто-Рико
Домашнее задание
Задача 1
Найдите на рисунке:
а) равные треугольники и обоснуйте
их равенство.
б) равнобедренные треугольники и
объясните, почему они являются
равнобедренными
B
Задача 2
От равностороннего треугольника,
площадь которого равна 36 см2,
отрезали три равных
равносторонних треугольника так,
что образовался правильный
шестиугольник. Найдите площадь
этого шестиугольника.
E
F
K
D
A
M
L
C
Указания к решению домашних
задач
Задача 2
B
Выполните дополнительные
построения, указанные на
рисунке.
F
E
O
D
A
M
K
L
C
Спасибо за
урок !