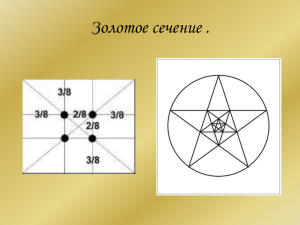
«ЗОЛОТОЕ СЕЧЕНИЕ»
реклама

«ЗОЛОТОЕ СЕЧЕНИЕ» О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Что же такое «золотое сечение»?.. Может быть, это закон красоты? Научное открытие или мистическая тайна? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно... И в этом его подлинная загадка, его великая тайна. На уроке мы раскроем тайны “золотого сечения”. Узнаем, что существует такая золотая точка на любом отрезке, которая обеспечивает, присутствие красоты, соразмерности всех частей, рассмотрим примеры где встречается “золотое сечение” в живой и не живой природе. Проведем практическую работу на нахождения “золотого сечения”. Мы попытаемся установить, есть ли что-то общее между древнеегипетскими пирамидами, картиной Леонардо да Винчи "Мона Лиза", подсолнухом, улиткой, сосновой шишкой и пальцами человека? Ответ на этот вопрос скрыт в удивительных числах, которые были открыты итальянским математиком Фибоначчи. После его открытия эти числа так и стали называться – числа Фибоначчи . Удивительная суть чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел: 1,1,2,3,5,8,13,21,34,55,… В числах Фибоначчи существует еще одна очень интересная особенность. При делении любого числа на число, стоящее перед ним, результатом всегда будет приближенно 1,62. Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. Отношение различных частей нашего тела составляют число, близкое к золотому сечению. Если эти значения совпадают со значением золотого сечения, то человек считается идеально сложенными. ПРАКТИЧЕСКОЕ ЗАДАНИЕ Найдите на руке или на лице размеры, соответствующие золотому сечению. ПРОВЕРЬТЕ: 1. Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца). 2. Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения. ПРОВЕРЬТЕ: На человеческом лице существует несколько правил золотого сечения. 1. Высота лица и ширина лица. 2. Ширина рта и ширина носа. 3. Расстояние между зрачками и расстояние между бровями. ЗОЛОТОЕ СЕЧЕНИЕ В МАТЕМАТИКЕ Возьмите отрезок длиной 100 мм и разделите его приблизительно в золотом отношении. ПРОВЕРЬТЕ: Длина одной части отрезка должна быть равна 62 мм, а второй части – 38 мм. Одна часть отрезка больше другой в 1,62 раза. ЗОЛОТОЙ ПРЯМОУГОЛЬНИК Если отношение длины прямоугольника к ширине равно 1,62, то такой прямоугольник называют ЗОЛОТЫМ. ПРАКТИЧЕСКОЕ ЗАДАНИЕ: Среди разложенных перед вами прямоугольников найдите золотые. Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. ПРАКТИЧЕСКОЕ ЗАДАНИЕ: Проверьте это! ЗОЛОТОЙ ТРЕУГОЛЬНИК Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в золотом сечении. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Например, отрезок АВ можно разделить на две части следующими способами: • На равные части – АВ : АС = АВ : ВС. • На две неравные части в любом отношении. • Так что, АВ : АС = АС : ВС. ЗОЛОТОЕ СЕЧЕНИЕ – это такое деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как большая часть относится к меньшей с : b = b : а. ПРАКТИЧЕСКОЕ ЗАДАНИЕ Разделите отрезок в золотом отношении. 1. Из точки В восставить перпендикуляр, равный половине АВ: BC = 1/2 AB. 2. Полученную точку С соединить линией с точкой А. 3. На полученной линии отложить отрезок СD = ВС. 4. На прямой АВ отложить отрезок АЕ = AD. Полученная при этом точка Е делит отрезок АВ в золотом отношении. Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. СПИРАЛЬ Лежащее в основе строения спирали правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях. Самые наглядные примеры - спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестков роз и т.д. ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев напоминают форму оси, склонной обратиться в спираль. Пауки всегда плетут свои паутины в виде спирали. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38. Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения. ЗОЛОТОЕ СЕЧЕНИЕ В КАРТИНЕ Леонардо да Винчи "Джоконда" Портрет Моны Лизы привлекает тем, что композиция рисунка построена на «золотых треугольниках». ЗОЛОТОЕ СЕЧЕНИЕ В КАРТИНЕ И. Шишкина"Сосновая роща" Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕ Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самая знаменитая из них была статуя Зевса Олимпийского, которая считалась одним из чудес света и статуя Афины Парфенос.