Транспортная задача - Томский политехнический университет

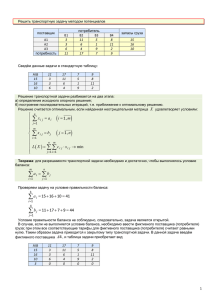
Транспортная задача
частный случай
задачи линейного программирования
Построить экономико-математическую
модель следующей задачи:
Имеются 3 поставщика и 4 потребителя.
Мощность поставщиков и спросы
потребителей, а также затраты на
перевозку единицы груза для каждой
пары «поставщик – потребитель»
сведены в таблицу поставок.
В каждой клетке стоит коэффициент
затрат – затраты на перевозку единицы
груза от соответствующего поставщика
к соответствующему потребителю.
Транспортная задача
Потребители и их спрос
Мощность
Поставщики поставщико
в
1
20
1
1
2
х11
60
1
2
100
х12
х21
120
х22
3
х14
2
х24
х23
7
х32
4
110
х13
5
3
х31
3
40
5
6
6
3
2
110
х33
4
х34
Транспортная задача
Найти объем перевозок для каждой пары
«поставщик – потребитель» так, чтобы:

мощность всех поставщиков были реализованы;

спросы всех потребителей удовлетворены;

суммарные затраты на перевозку были
минимальными.
Экономико-математическая
модель задачи
f(х) = 1x11+2x12+5x13+…+7x33+4x34 → min
 x11  x12  x13  x14  60

 x21  x22  x23  x24  120
 x  x  x  x  100
33
34
 31 32

 x11  x21  х31  20

 х12  x22  х32  110
 х13  x23  х33  40

 х14  x24  х34  110
Особенности экономико-математической
модели транспортной задачи
Система ограничений есть система
уравнений, то есть транспортная задача
задана в канонической форме.
 Коэффициенты при переменных системы
ограничений равны 1 или 0.
 Каждая переменная входит в систему
ограничений 2 раза.

Два метода нахождения
первоначального распределения
поставок (опорного плана)

Метод северо-западного угла

Метод минимальной стоимости (или метод
наименьших затрат)
Важно помнить
Обязательно вычеркивается только один:
или поставщик, или потребитель.
Если на очередном шаге решения задачи совпали
потребность покупателя и мощность поставщика,
то одного (любого) вычеркиваем, а у второго
пишем в остатке 0.
На следующем шаге решения перевозим 0, тогда
эта клетка участвует в плане перевозок.
Если этого не сделать, то в плане будет
недостаточно клеток, чтобы заполнить таблицу
потенциалов.




Алгоритм
а) Вписываем в таблицу стоимости перевозок,
соответствующих опорному плану;
б) Задаем произвольно один из потенциалов и
вычисляем остальные, учитывая, что сумма
потенциалов равна стоимости перевозки;
в) Вычисляем косвенные стоимости (суммируем
соответствующие потенциалы и заполняем
свободные клетки таблицы), помечаем косвенные
стоимости штрихом;
г) Находим разницу между стоимостью, заданной в
задаче, и косвенной стоимостью;
Алгоритм
 д) Выберем максимальную отрицательную разность
и введем ее в опорный план, то есть увеличивая ее
значение на какую-то величину, тогда значение
другой переменной должно уменьшиться на эту же
величину и так далее, замыкаем цикл. (Этот
процесс называется цикл пересчета).
 е) Если отрицательных значений нет, значит
найденный опорный план является оптимальным.
 ж) Определяем максимальную величину, на
которую может быть увеличена клетка, вводимая в
опорный план, так чтобы количество перевозки не
стало отрицательным.
Важно помнить
На каждом шаге решения задачи одна
перевозка входит в опорный план и одна выходит
из него.
Количество клеток, участвующих в плане
перевозок, в ходе решения задачи не меняется.
Если получается две клетки с одинаковыми
минимальными значениями, помеченными знаком
«–», то одна выходит из опорного плана, а во
второй (в любой) остается 0, то есть клетка
участвует в плане перевозок
Важно помнить

Метод потенциалов позволяет решать только
сбалансированные задачи, то есть задачи,
в которых суммарная мощность поставщиков
равна суммарному спросу потребителей.

На практике такая ситуация встречается редко,
поэтому любую транспортную задачу можно
привести к сбалансированной.
Задача на недостаток
Если в транспортной задаче суммарная
мощность поставщиков меньше суммарного
спроса потребителей, то такая задача называется
задачей на недостаток.
Для ее решения необходимо ввести фиктивного
поставщика, стоимости перевозок которого будут
равны нулю, а мощность равна разности
суммарного спроса потребителей и суммарной
мощности действительных поставщиков, то есть
размеру недостатка.
Задача на избыток
Если в транспортной задаче суммарный спрос
потребителей меньше суммарной мощности
поставщиков, то такая задача называется
задачей на избыток.
Для ее решения необходимо ввести фиктивного
потребителя, стоимости перевозок которого будут
равны нулю, а мощность равна разности
суммарной мощности поставщиков и суммарного
спроса действительных потребителей, то есть
размеру избытка.

Когда задача решена, цифры в строке
фиктивного поставщика показывают, какое
количество продукции, кто из потребителей не
получит, так как задача была на недостаток.


Когда задача решена, цифры в строке
фиктивного потребителя показывают, какое
количество продукции, у кого из поставщиков
останется, так как задача была на избыток.
СПАСИБО ЗА ВНИМАНИЕ!
к.т.н., доц. Калашникова Т.В.
[email protected]