1.Магнитное поле и его характеристики

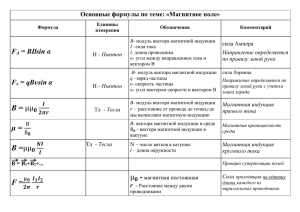
Лекция №13
Тема: «МАГНЕТИЗМ»
1.Магнитное поле и его характеристики.
2.Напряжённость магнитного поля. Формула Ампера. Закон
Био-Савара-Лапласа.
3.Магнитная индукция.
4.Поток вектора магнитной индукции. Теорема Гаусса для вектора
магнитной индукции.
5.Формула Лоренца для силы действующей на заряд со
стороны электрического и магнитного полей.
6.Диамагнитные, парамагнитные, ферромагнитные вещества.
7.Магнитная проницаемость.
8.Взаимная индукция, Трансформатор, физические принципы
его действия.
9.Энергия магнитного поля. Электромагнитная теория
Максвелла.
10.Взаимосвязь электрических и магнитных величин
1.Магнитное поле и его характеристики
В XVIII веке было обращено внимание на
намагничивание железных предметов и перемагничивание
компаса вблизи грозового разряда. Это наводило на мысль
о связи магнитных явлений с электрическими. Это
подтвердил датский физик Х.К. Эрстред. Он установил,
что электрический ток воздействует на расположенную
поблизости магнитную стрелку, ориентируя её
перпендикулярно проводу. Тогда же французский физик
Ампер экспериментально обнаружил магнитное
взаимодействие двух проводников с током.
Следовательно вокруг движущихся электрических
зарядов (токов) возникает ещё один вид поля- магнитное
поле , по средствам которого эти заряды взаимодействуют
с магнитными или другими движущимися
электрическими зарядами.

Так как магнитное поле
является силовым полем,
то его можно изобразить
силовыми линиями,
например: магнитное
поле стержневого
магнита
Магнитное поле
созданное током I в
прямолинейном
проводнике (опыт
Эрстреда)
Силовые линии представляют собой
концентрические окружности, перпендикулярные
проводу, центры которых находятся на этом проводе.
Направление силовых линий магнитного поля
определяется правилом буравчика: рукоятка буравчика,
ввинчиваемого по направлению тока, вращается в
направлении магнитных силовых линий.
В отличии от силовых
линий электрического
поля магнитные силовые
линии всегда замкнуты.
Они не имеют ни начала
ни конца.
2.Напряжённость магнитного поля. Формула
Ампера. Закон Био-Савара-Лапласа.
Для количественной характеристики магнитного поля
служит величина, получившая название напряженность
магнитного поля Н.

dH
α
dl
r

I1dl1
dH  k
r2
Эта величина
 зависит только от элемента
тока I1d l1 и положения той точки, где
находится элемент тока.
Закон Био-Савара-Лапласа для элемента тока
dH
I
R
A
α
dα
r
dl

Вектор напряженности магнитного
поля перпендикулярен плоскости в
которой лежат вектора элемента тока
и радиус- вектор данной точки.
Модуль вектора напряженности
магнитного создаваемого элементом
тока определяется по формуле
i  d  l  sin 
dH 
2
4   r
(2)
Этот закон позволяет рассчитать полную напряжённость
магнитного поля для проводника любой формы.
Закон Ампера с учётом напряжённости
dF  0  I  I 0  dl  dl0  sin   sin 
где β- угол между направлениями тока I0 и магнитного поля dH.
Определим направление силы dF по правилу левой руки

Если ладонь левой руки так, чтобы вектор напряжённости
магнитного поля входил в ладонь, а четыре вытянутых
пальца направлялись вдоль тока, от отставленный большой
палец покажет направление силы, действующей на этот ток.
1
dF
dH 

 0 I 0  dl 0
 0 - магнитная постоянная,
 0  4    10
7
Ги
м
Физический смысл:
Напряжённость магнитного поля направлена по
касательной к силовой линии поля, а по модулю равна
отношению силы, с которой поле действует на единичный
элемент тока (расположенный перпендикулярно полю в
вакууме), к магнитной постоянной.
H   dH 
l
1
4 
I  sin 
l r 2  dl
3.Магнитная индукция
Магнитное поле, не изменяющееся с течением времени,
называется стационарным.
Возникновение магнитного поля видно из
опыта Эрстреда.
Если магнитную стрелку, которая может свободно
вращаться вокруг вертикальной оси поместить под
прямолинейным проводником с постоянным током, то
она стремится расположиться перпендикулярно
проводнику с током. Чем больше сила тока, чем ближе
стрелка и меньше влияние магнитного поля Земли, тем
точнее расположиться стрелка.
.
Силовой характеристикой магнитного поля является

вектор магнитной индукции B
B   0  E


B    0  H
Где H  результирующая напряжённость
2
1
B



H

м

кг

с

А
0
Размерность индукции
А  м 1  кг  с 2  А1  Тл - Тесла


Направление вектора индукции B совпадает с
вектором напряжённости H в однородной изотропной
среде.
1 Тл – магнитная индукция такого однородного
магнитного поля которое действует с силой 1 Н на
прямоугольный проводник длинной один метр с током в 1
А расположены перпендикулярно полю.
4.Поток вектора магнитной индукции.

Теорема Гаусса для вектора B
Потоком вектора магнитной индукции (магнитным потоком )
через площадку dS называется
величина
dФ  B  dS  cos 
Поток вектора В величина
скалярная.
Ф 
B
S
n
 dS
Поток вектора магнитной индукции через произвольную
поверхность S определяется по формуле:
Теорема Гаусса для поля вектора B
поток вектора магнитной индукции через любую
замкнутую поверхность всегда равен нулю, т.е.
Ф
 B  dS
0
S
B
Это связано с тем, что линии
магнитной индукции замкнуты и
поэтому число линий входящих в
поверхность с одной стороны,
равно числу линий выходящих с
другой стороны.
5.Формула Лоренца для силы, действующей на
заряд со стороны электрического и магнитного
полей
Закон Ампера
на участок проводника длинной , по которому течёт ток
силой I со стороны внешнего магнитного поля
напряжённостью H действует сила:
F  I  l  H  sin 
где α – угол между направлением тока и напряжённости
магнитного поля

Сила тока I численно равна заряду, перенесённому в
единицу времени через поперечное сечение проводника.
Если величина отдельного заряда e , а число зарядов
перенесённых через поперечное сечение проводника в
единицу времени = n, то I  e  n следовательно:
n  n0  v  S
где n0 – число движущихся зарядов в единице объёма, v – их
скорость, S – площадь поперечного сечения.
I  e  n0  v  S
F  e  n0  v  S  l  H  sin 
n  n0  S  l
F 
F
F
e  n0  v  S  l  H  sin 


n n0  S  l
n0  S  l
Формула Лоренца
F  e  v  H  sin 
F - исходная сила, действующая
на заряд, движущийся со
скоростью v в магнитном
поле напряжённостью H.
В случае движения положительного заряда направление
силы Лоренца определяется направлением левой руки:

Если сложенные вместе
пальцы поместить по
направлению движения
заряда, а ладонь расположить
так чтобы линия
напряжённости магнитного
поля входила в ладонь то сила
F будет направлена в сторону
оттопыренного большого
пальца, а при движении
отрицательного заряда сила
F будет направлена в
противоположную сторону.
6.Диамагнитные, парамагнитные,
ферромагнитные вещества. Магнитная
проницаемость.

Диамагнитные свойства наблюдаются у веществ атомы
которых имеют магнитный момент ; равный нулю
(неполярные диэлектрики), например, Bi,Ag,Cu,
большинство органических соединений, углекислый газ.
eB

2m

- Ларморовая частота. Она не зависит от угла наклона α
и одинакова для всех электронов.
 m  0,   1

Парамагнитные свойства наблюдаются у веществ, атомы
которых имеют отличный от нуля магнитный момент
(полярные диэлектрики). В отсутствии внешнего
магнитного поля, вследствие теплового движения,
магнитные моменты атомов разориентированы и поэтому
магнитный момент вещества равен нулю.
 m  0,   1
В парамагнетиках наблюдается и диамагнитный эффект, но
он значительно слабее парамагнитного и им можно
пренебречь.
Парамагнетики и диамагнетики относятся к слабомагнитным
веществам, но существуют и сильномагнитные вещества ферромагнетики у которых   1 (железо, никель,
кобальт, гадолиний, их сплавы и соединения).
Ферромагнетики помимо способности сильно
намагничиваться обладают еще и другими свойствами,
существенно отличающими их от диа - и парамагнетиков.


всего нелинейная зависимость j от H или
Это, прежде

B от H
При возрастании
намагниченность сначала
растет быстро, затем рост
замедляется и, наконец,
достигается так называемое
магнитное насыщение уже не
зависящее от напряженности
магнитного поля .
Вторая особенность ферромагнетиков:магнитная
проницаемость μ не только имеет большие значения (для
железа - 5000, для сплава супермаллоя - 800000), но и
зависит от напряженности внешнего магнитного поля .
Вначале μ растет с увеличением Н, затем, достигая
максимума, начинает уменьшаться, стремясь в случае
сильных полей к 1

Характерная особенность
ферромагнетиков состоит в том, что для
них зависимость j от Н определяется
предысторией образца. Это явление
магнитного гистерезиса.
Магнитное действие тока
I1  
H  k
r2
1
F
H
I2  
1
k
4
2