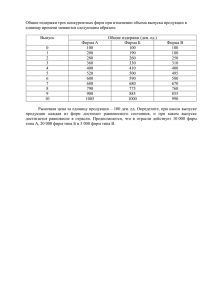
равновесное и общественно эффективное число

Ограничение конкуренции
на отраслевых рынках:
равновесное и общественно
эффективное число фирм
Макольская Я.С., Филатов А.Ю.
Иркутский государственный университет
http://matec.isu.ru, http://math.isu.ru/filatov,
http://polnolunie.baikal.ru/me, http://fial_.livejournal.com,
[email protected], [email protected]
Олигополия
Особенности:
1. Небольшое количество фирм (максимальное число которых зависит от
информационной открытости рынка).
2. Однородный (нефть) либо дифференцированный (сотовая связь) продукт.
3. Стратегическое взаимодействие между производителями.
4. Наличие барьеров входа.
Олигополия без сговора – каждая из фирм, ориентируясь на действия конкурентов, самостоятельно максимизирует прибыль, управляя своей ценой и
объемом поставок продукции.
Виды олигополии без сговора:
1. Количественная олигополия (более адекватна в ситуации, когда фирмам
после принятия плана относительно трудно изменить производственные
мощности, а, следовательно, и объем поставок).
2. Ценовая олигополия (более адекватна, когда фирмы в состоянии за небольшое время существенно изменить объем поставок, в том числе, при
возможности, завоевать весь рынок).
Модель Курно (1838)
n олигополистов с объемами поставок продукции q1,...,qn и функциями
издержек TC1q1 ,...,TCn qn . Отраслевой спрос задан некоторой функцией
Q  D p   p  D 1 Q . Прибыль каждого i-олигополиста зависит от объемов
поставок конкурентов q i и составляет


 i qi , qi   TRi qi , qi   TCi qi   pqi  TCi qi   D 1 qi   q j  qi  TCi qi   max .

j i

qi
Кривые реакции – оптимальные отклики каждого олигополиста на меняющиеся условия функционирования рынка
qi q1,...,qi 1, qi 1,...,qn .
Пересечение кривых реакции – равновесие Нэша (ситуация, в которой
ни одному из участников рынка невыгодно в одностороннем порядке менять собственную стратегию поведения).
Недостаток модели Курно: экзогенно задаваемое число фирм на рынке
При отсутствии барьеров входа положительные прибыли означают вход
новых фирм на рынок.
В реальной экономике вход ограничен наличием постоянных издержек.
Концентрация фирм на рынке
Показатели концентрации:
1. Индекс концентрации CRk – сумма рыночных долей крупнейших компаний,
действующих на рынке. CRk   yi .
2. Индекс Линда ILk – показатель, ориентированный на учет различий в ядре.
y1
 y  y2   2 ,
1
y1
, IL3  
 1

y2
2   y2  y3  2
y3

 y  y  2   y1  y2  y3 
1
y1
IL4  
 1 2
3   y2  y3  y4  3  y3  y4  2
y4
IL2 
3
.

3. Индекс энтропии E – средняя доля фирм, действующих на рынке, взвешенная по логарифму обратной величины E   yi ln 1 yi .
4. Индекс Херфиндаля-Хиршмана HHI – сумма квадратов долей всех компаний, действующих на рынке HHI   yi2  0; 10000 .
Низкая степень концентрации: CR3  45%, HHI  1000 .
Средняя степень концентрации: 45%  CR3  70%, 1000  HHI  2500 .
Высокая степень концентрации: CR3  70%, HHI  2500 .
Россия, эмпирические данные
Современное состояние рынков и тенденции (С.Авдашева):
1. Концентрация в большинстве отраслей соответствует мировому уровню.
При этом CR4 примерно на 10 пунктов выше, чем в США, однако настолько же ниже, чем в Японии.
2. На высококонцентрированных рынках концентрация незначительно снижается, на низкоконцентрированных – повышается.
3. Показатели концентрации в долгосрочной перспективе устойчивы. При
этом наблюдается перераспределение рынка между производителями, в
том числе, за счет входа/выхода фирм.
Табл.1. Россия, химическая и нефтехимическая промышленность:
Высококонцентр. CR3 HHI Среднеконцентр. CR3 HHI Низкоконцентр. CR3 HHI
Горнохимическая
Содовая
Химико-фотографич.
Пр-во калийн. удобр.
93,8
100,0
87,8
100,0
4931 Пр-во синт. красит.
4369 Пр-во синт. каучука
5636
Пр-во шин
3682 Пр-во изд. из пласт.
59,0
65,6
52,7
57,2
1570
Азотная
40,4 938
2151
Лакокрасочная
32,1 632
1358 Химико-фармацевт. 27,0 462
2459
Барьеры входа
Входной барьер – всё, что позволяет укоренившимся фирмам получать сверхприбыли без угрозы входа.
Барьеры, устанавливаемые государством (лицензии, патенты, разрешения).
## Продажа лицензий на предоставление услуг мобильной связи (в т.ч., 3G).
Барьеры, не связанные с деятельностью государства (абсолютные преимущества в издержках, эффект масштаба, доступ к ресурсам и технологиям…)
## «Polaroid» – ограничение доступа на рынок моментальной фотографии.
Блокированный вход. Укоренившиеся фирмы конкурируют, не обращая внимания на возможный вход новичков. Но даже отсутствие специальных мер, ограничивающих вход, не делает рынок привлекательным для новых фирм.
Сдерживаемый вход. Вход невозможно блокировать, но укоренившиеся фирмы модифицируют свое поведение, чтобы эффективно мешать входу.
Предоставляемый вход. Укоренившиеся фирмы (каждая в отдельности) находят более выгодным позволить новичкам войти, нежели возводить дорогостоящие входные барьеры.
Равновесие ≠
≠ общественная эффективность
Примеры:
1. Дилемма заключенного (доминирующие стратегии ведут к худшему исходу).
Не созн.
Созн.
Не созн.
15сут. / 15сут.
10 лет / 0
Созн.
0 / 10 лет
5 лет / 5лет
Дорого
Дешево
Дорого
5 млн. / 5 млн.
0 / 6 млн.
Дешево
6 млн. / 0
2 млн. / 2 млн.
2. Недофинансирование общественных благ.
3. Трагедия общины (истощение ресурсов из-за чрезмерного использования).
4. Асимметричность информации (отрицательный отбор, моральный риск).
Вопрос: могут ли барьеры увеличивать общественную эффективность?
Увеличение числа фирм:
+ усиление конкуренции, снижение цен, расширение продаж.
– многократно дублирующиеся постоянные издержки производства.
Модель с линейными издержками
Предположения модели:
1. Линейный отраслевой спрос p  a  bQ.
2. n одинаковых олигополистов с линейными издержками TCi qi   cqi  f .
3. Олигополисты конкурируют по объемам.
4. Количество фирм n определяется эндогенно из условия нулевой прибыли.
Равновесное число фирм на рынке
Максимизация прибыли:


 i qi , qi   pqi  TCi qi    a  bqi  b q j qi  cqi  f  max ,
qi
j i


a  2bqi  b q j  c  0.
Равновесные значения объемов поставок, цен и прибылей:
1 ac
n ac
q* 
, Q* 
,
n 1 b
n 1 b
a  c   f .
1
n
p* 
a
c,  *  p * q * cq *  f 
n 1
n 1
n  12 b
Равновесное число фирм на рынке:
 *  0,
a  c 2  bf ,
n  12
n1 
a  c 2
bf
j i
 1.
2
Общественно эффективное
число фирм на рынке
Общественное благосостояние = потребительский излишек + прибыль:
1
a  p *nq *  n * 
2
2
2
2
 n  a  c  na  c 


 nf 

2b
n  12 b
 n  1
2

a  c  n 2  2n

 nf 
2b n  12
2

a  c 
1 
1 
  nf  max .

n
2b  n  12 
SW  RD  n * 
2
2


a  c
a  c
3
SW  
 f  0, n  1 
.
3
bf
bn  1
2
2




a

c
a

c
n 3
1 
1  n
2
bf
bf
1
p
a
RD
p*
n ( + f )
c
Q
(a – p*)/b
– общественно эффективное число фирм
меньше равновесного!
Ситуация сговора
Оптимальный объем поставок при сговоре n одинаковых фирм:
  a  bnqq  cq  f  max , a  2bnq  c  0.
2

ac
ac q
ac
a  c
q* 
, Q* 
, p* 
, * 
 f.
2bn
2b
2
4bn
Общественное благосостояние при сговоре n одинаковых фирм:
a  c   a  c  n  nf  3 a  c   nf , SW  при n
1
SW  a  a  c  2
2
2b
4bn
8 b
2
2
Численный пример – 1
p  55  Q, TC(q)  25  15q.
Равновесное число фирм: n1  7. Общественно эффективное число фирм: n2  3.
n
q
Q
p
П
RD nП SW
n
q
Q
p
П
RD nП SW
7
5
35
20
0
613
613
7
2,86
20
35
32
200 225 425
3
10
30
25
75
450 225 675
3
6,67
20
35
108
200 325 525
1
20
20
35
375
200 375 575
1
20
20
35
375
200 375 575
0
Объемы, цены, благосостояние
в модели олигополии без сговора
Объемы, цены, благосостояние
в модели олигополии со сговором
Издержки вероятного сговора
при сократившемся числе фирм
Переход от конкуренции равновесного числа фирм к сговору эффективного
числа фирм:
1 a  c  1 a  c 
1 a  c  1
SWб / сг n1  


n
f

 f 
1
2 b
2 n1  12 b
2 b
2
2
2
2


3 a  c 
3 a  c 
a

c
SWсг ов n2  
 n2 f 
 f 3
f.
8 b
8 b
bf
2
2
2
a  c 2 f .
b
SWсгов n2   SWб / сг n1   0
a  c  .
1
1
SWсг ов n2   SWб / сг n1    x  f  xf  3 xf 2 , x 
8
2
b
SWсг ов n2   SWб / сг n1 
1 1
f
fb
gy 
   y  y  3 y2 , y  
 1.
2
x
8 2
x a  c 
1
1
2
1
3
g  y   

 0, g  y  , g 0    0, g 1   0.
2 2 y 33 y
8
8
2
g  y *  0,
y*  0,064.
2

a  c

2 y*  0,128 * RD
При высоких постоянных издержках f
CK даже сговор
2b
оказывается предпочтительнее конкуренции равновесного числа фирм.
Издержки вероятного сговора
при сократившемся числе фирм
Переход от конкуренции равновесного числа фирм к монополии:
1 a  c  1 a  c 
1 a  c  1
SWб / сг n1  


n
f

 f 
1
2
2 b
2 n1  1 b
2 b
2
2
3 a  c 
SWмон 
 f.
8 b
2
2
2
a  c 2 f .
b
SWмон  SWб / сг n1   0
a  c  f .
1 a  c  3
SWмон  SWб / сг n1   
 f 
8 b
2
b
SWмон  SWб / сг n1 
1
3
ac
g z  
  z 2   z, z 
.
f
8
2
bf
2
1
3
g z   0,  z 2  z   0,
8
2
2
2

a  c
z  2; 6,
 36 .
bf
1 a  c 
1
f  *
 * RDCK  0,056 * RDCK моно18
2b
18
2
При высоких постоянных издержках
полия оказывается предпочтительнее конкуренции равновесного числа фирм.
Модель с квадратичными издержками
Численные примеры
p  55  Q, TC (q)  25  15q  3q 2 .
Равновесное число фирм: n1  9. Общественно эффективное число фирм: n2  7,9.
n
q
9
2,5
7,9
2,7
1
5
П
RD
nП
SW
n
q
Q
p
П
RD
nП
SW
22,5 32,5
0
253
0
253
9
1,7
15
40
8,3
113
75
188
21,2 33,8
3,8
225
30
255
7,9
1,8
14,5 40,5 11,7
105
92
197
75
13
75
88
1
5
13
75
88
Q
5
p
50
Объемы, цены, благосостояние
в модели олигополии без сговора
5
50
75
Объемы, цены, благосостояние
в модели олигополии со сговором
p  55  Q, TC (q)  110  23q  0,1q 2 .
Равновесное число фирм: n1  2. Общественно эффективное число фирм: n2  1,174.
n
q
Q
p
П
RD
nП
SW
n
q
2
10
20
35
0
200
0
200
2
7,6
90
125
106
231
123
106
123
229
1,2 13,5 15,8 39,2
1
14,5 14,5 40,5
П
RD
nП
SW
15,2 39,8
12
116
24
140
1,2
12,6 14,7 40,3
91
109
107
215
1
14,5 14,5 40,5
123
106
123
229
Q
p
Модель с квадратичными издержками
Предположения модели:
1. Линейный отраслевой спрос p  a  bQ.
2. n одинаковых олигополистов с квадратичными издержками TCi qi   dqi2  cqi  f .
3. Олигополисты конкурируют по объемам.
4. Количество фирм n определяется эндогенно из условия нулевой прибыли.
Максимизация прибыли:


 i qi , qi   pqi  TCi qi    a  bqi  b q j qi  dqi2  cqi  f  max , a  2bqi  b q j  2dqi  c  0.
qi
j i
j i


Равновесные значения объемов поставок, цен и прибылей:
a  c  b  d   f .
ac
nba  c 
2
q* 
, p*  a  bQ*  a 
,  *  p * q * d q *  cq *  f 
nb  b  2d
nb  b  2d
nb  b  2d 2
2
Равновесное число фирм на рынке:
 *  0,
a  c 
bd

nb  b  2d
f , n1 
a  c 
b  d b  2d

.
b
b f
Свойство:
bd
,
Если постоянные издержки не выше критического уровня f  a  c 2
2
b  2d 
на рынке работает положительное количество фирм n1  0.
Модель с квадратичными издержками
Функция общественного благосостояния:
1 n 2ba  c 
na  c  b  d 
SW 

 nf  max .
2
2
n
2 nb  b  2d 
nb  b  2d 
2
3 a  c 
SW '  dx  bb  2d   kx
, x  nb  b  2d ,
3
2
x


k

f
a

c
.
3
x
g x  
SW '  dx  bb  2d   kx3.
2
a  c 
2

g(x(n))
2

b(b+2d)
При g(x) > 0 SW, при g(x) < 0 SW,
при g(x) = 0 SW достигает максимума.
xn1  
b  2d   b  2d  a  c  b  d .
ba  c  b  d
b
b
b f
f
a  c 
g  xn1   d
При
f  a  c 
bd
f
x(n1) x(n)
d 3k
SW
x(n2)
SW
3


f
a  c  b  d  b  d
bd



 b  2bd 

b
b

2
d

a

c

f f
f
a  c 2

2

.


bd
(условии выгодности работы фирм на рынке) g xn1   0.
b  2d
С учетом монотонности перехода от n к x(n) n1  n2 – общественно эффективное число фирм всегда меньше равновесного и для квадратичных издержек!
Выводы
1. С точки зрения максимизации общественного благосостояния на рынке
должно находиться меньше, чем в равновесии, более крупных, чем в равновесии, фирм.
2. Вывод применим не только к линейным издержкам, для которых справедлива возрастающая отдача от масштаба, но и к квадратичным функциям
общего вида, для которых с некоторого объема производство становится
заведомо невыгодным даже при фиксированных ценах.
3. Ограничения входа, инициируемые укоренившимися фирмами, не всегда
уменьшают общественное благосостояние.
4. В некоторых случаях целесообразно не стимулировать избыточную конкуренцию, а напротив, ограничивать вход на рынок новых компаний.
5. При малых постоянных издержках значительную опасность представляет
увеличение вероятности сговора при ограничении числа фирм. При высокой доле постоянной составляющей в издержках их уменьшение является
более важным, чем возможный сговор.
6. При ограничении входа через систему лицензирования важным является
недопущение коррупции, весьма вероятной при распределении лицензий
чиновниками, а не через аукцион.
Спасибо
за внимание!
http://matec.isu.ru, http://math.isu.ru/filatov,
http://polnolunie.baikal.ru/me, http://fial_.livejournal.com,
[email protected], [email protected]