МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 2 Основные темы • :

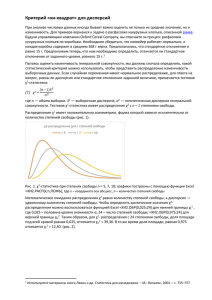
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 2
Основные темы
• Проверка статистических гипотез
•Критерии согласия:
• Критерий Пирсона (хи-квадрат),
• Критерий Колмогорова.
•Параметрические критерии:
•Критерий Фишера (сравнение дисперсий);
• Сравнение математических ожиданий
• при больших и малых объёмах выборок.
• Ранговые критерии
• Однофакторный дисперсионный анализ
• Элементы теории корреляции
Проверка статистических гипотез
§ Основные сведения
Статистической гипотезой называется любое
предположение о виде или параметрах неизвестного
закона распределения.
Проверяемую гипотезу называют нулевой (основной),
обозначают её Н0.
Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой, обозначают её Н1.
Задача: проверить, верна ли нулевая гипотеза Н0 при
альтернативной гипотезе Н1?
Гипотеза Н0
Принимается
Отвергается
Верна
Правильное решение
Ошибка 1-го рода
Неверна
Ошибка 2-го рода
Правильное решение
Обозначим через  – вероятность допустить ошибку
1-го рода, через  – вероятность ошибки 2-го рода.
Вероятность  допустить ошибку 1-го рода, то есть
отвергнуть верную гипотезу Н0, называют уровнем
значимости.
1. Задаём уровень значимости  .
2. Строим случайную величину K, называемую статистическим критерием, для которой выполняются следующие условия:
1) она является функцией от выборочных данных:
K=K(x1,x2,…,xn);
2) её значения позволяют судить о «расхождении
выборки с гипотезой Н0», то есть о том, надо принимать или отвергать гипотезу H0;
3) распределение этой величины известно.
3. Вычисляем значения критерия, подставляя в него
выборочные данные. Это число называют наблюдаемым значением критерия и обозначают Kнабл.
4. Находим критическую область данного критерия,
то есть совокупность значений критерия,
при которых нулевую гипотезу отвергают.
Все остальные значения критерия образуют область,
называемую областью принятия нулевой
гипотезы.
5. Если наблюдаемое значение критерия попадает в
критическую область, то нулевую гипотезу
отвергаем, в противном случае нулевую гипотезу
принимаем.
Точки, которые отделяют критическую область от
области принятия гипотезы, называют критическими
точками.
Чаще всего встречаются следующие виды критических
областей:
а) левосторонняя
K < kкр
kкр
б) правосторонняя
K > kкр
kкр
в) двусторонняя
K < kкр1
kкр1
kкр2
K > kкр2
Критическую область W целесообразно находить
согласно следующим требованиям:
1. p( K  W )  
2. вероятность  ошибки 2-го рода – минимальная,
то есть вероятность (1   ) – максимальная
Вероятность (1   ) не допустить ошибку 2-го рода,
то есть отвергнуть гипотезу H0, когда она неверна,
называется мощностью критерия.
Мощность критерия – максимальная.
• При разработке статистического
критерия невозможно одновременно
минимизировать обе ошибки. Поэтому
поступают следующим образом: при
заданном числе испытаний n
устанавливается верхняя граница для
ошибки первого рода.
• Выбирается тот критерий, у которого
наименьшая ошибка второго рода.
Пять шагов проверки
гипотезы
1. Сформулировать нулевую H0 и альтернативную H1
гипотезы.
2. Выбрать статистику критерия T(X) и уяснить её закон
распределения.
.
3. Задать уровень значимости критерия По таблицам
квантилей распределения статистики найти критические
точки и указать критическую область.
4. Подсчитать наблюдаемое значение статистики
критерия и проверить условие его попадания в
критическую область.
5. Сделать вывод о принятии нулевой или альтернативной
гипотезы.
Критерии, с помощью которых проверяется гипотеза
о теоретическом законе распределения, называются
критериями согласия.
H0: генеральная совокупность имеет некоторое
определённое распределение
Параметрические критерии тестируют гипотезы
о параметрах некоторого распределения :
1. Генеральная совокупность имеет биномиальное
распределение с параметрами m = 10 и p = 0.4.
2. Генеральная совокупность распределена нормально
с математическим ожиданием, равным 5 и дисперсией,
равной 4.
§ Критерий согласия Колмогорова
Нулевая гипотеза: исследуемая случайная величина
имеет заданный закон распределения.
F(x) – теоретическая функция распределения
Fn(x) – эмпирическая функция распределения
Обозначим D  max Fn ( x)  F ( x)
– статистика критерия Колмогорова
Критерий:   D n
Критическая область W – правосторонняя:
кр
Из требования для критической области:
p ( W )  p (  кр )  p( D n  кр )  
1
0.8
0.6
i
N
c no rm Xi 0.4
( )
0.2
0
Xi
13
Можно доказать, что при n  
p( D n  кр )  p(кр )  1 
 1

(1)
2
2

2
k

k
кр
e



(1)
2
2

2
k

k
кр
e
k  
кр
k  

0.4
0.3
0.2
0.1 0.05 0.025 0.01 0.005 0.001 0.0005
кр 0.89 0.97 1.07 1.22 1.36 1.48 1.63 1.73
1.95
2.03
15
§ Критерий согласия Пирсона (хи-квадрат)  2
Найдём теоретические частоты вариант.
1. Распределение дискретное  p(x).
xi
x1
x2
…
xl-1
xl
pi p1=p(x1) p2=p(x2) … pl-1=p(xl-1) pl=1-p1-p2-…-pl-1
Теоретическая частота появления варианты xi – это npi.
2. Распределение непрерывное  F(x).
xi
(x1, x2)
(x2, x3)
…
(xl-1, xl)
(xl, xl+1)
pi p1=p(X< x2) p2=p(x2<X<x3) … pl-1=p(xl-1<X<xl) pl=1-p1-p2…-pl-1
=F(x2)
=F(x3)- F(x2)
=F(xl)- F(xl-1)
Теоретическая частота попадания в интервал (xi, xi+1) –
это npi.
Критерий:
2
(
n

np
)
i
2   i
npi
i 1
l
ni – эмпирические частоты
npi – теоретические частоты
При n   случайная величина  2 имеет распределение Пирсона с k степенями свободы, где
k = l – r –1,
l – число вариант (интервалов),
r – число параметров предполагаемого
распределения, оцениваемых по выборке.
Критическая область W – правосторонняя:
2
 кр
Из требования для критической области:
p(  2 W )  

2
p(  2   кр
) 
2
2
p (  2   кр
)  1  p(  2   кр
)  1
2
2
p (  2   кр
)  F (  кр
), F(x) – функция распределения  2
2
F (  кр
) 1

2
 кр
 F 1 (1   )
F(x) – функция распределения Пирсона с k= l – r –1
степенями свободы, l – число вариант (интервалов),
r – число параметров, оцениваемых по выборке.
Для нахождения критической области необходимо по
заданной вероятности ошибки первого рода (уровню
значимости критерия)  найти квантиль хи-квадрат
распределения на уровне 1 -  .
1
1- 
Область
принятия
гипотезы
C
Критическая область
Алгоритм применения критерия согласия Пирсона
Подсчитываем значение статистики критерия и сравниваем
его с критической точкой. Если статистика критерия
попадает в критическую область,
2
то нулевая гипотеза:
C
исследуемая случайная величина
имеет заданный закон распределения
отвергается.
В противном случае она принимается на уровне значимости 
Критерий легко приспосабливается и для непрерывных
распределений путем их дискретизации.
Проверку гипотезы удобно совмещать с построением
гистограмм.
§ Критерий Фишера
Две генеральные совокупности X и Y распределены
нормально.
Проверить гипотезу: H 0 : D( X )  D(Y )
Обозначим nX – объём выборки из совокупности X,
nY – объём выборки из совокупности Y,
s2X и s2Y – исправленные выборочные дисперсии.
Критерий:
F
s 2X
sY2
F имеет распределение Фишера с (nX –1) и (nY –1)
степенями свободы
Критическая область строится в зависимости от вида
конкурирующей гипотезы.
1. H1 : D( X )  D(Y )
Критическая область W – правосторонняя:
0
fпр,кр
Так как s2X >0 и s2Y >0, то F >0  положительная часть
Из требования 1 для критической области:
p( F W )    p( F  f пр ,кр )  
p( F  f пр,кр )  1  p( F  f пр,кр )  1  
p( F  f пр,кр )  F ( f пр ,кр ), F(x) – функция распределения F
F ( f пр,кр )  1  
 f пр ,кр  F 1 (1   )
F(x) – функция распределения Фишера с (nX –1) и
(nY –1) степенями свободы
2. H1 : D( X )  D(Y )
Обозначим
1 sY2
F   2
F sX
H1 : D(Y )  D( X )
, F’ имеет распределение
Фишера с (nY –1) и (nX –1)
степенями свободы
 предыдущий случай:
 ,кр  F 1 (1   ), где F(x) –
f пр
0
функция распределения F’
f’пр,кр
 ,кр )  
p( F   f пр
 ,кр )  p( F  1 / f пр
 ,кр )
 ,кр )  p(1 / F  f пр
p( F   f пр

 ,кр )  
p( F  1 / f пр
 ,кр )  
p( F  1 / f пр
Обозначим
 ,кр  1 / f пр
 ,кр , тогда
f лев
p( F  f лев ,кр )  
Таким образом, критическая область для критерия F
имеет вид:
0
 ,кр
f лев
fлев,кр
1
1
, где F(x) – функция

 1
 ,кр F (1   )
f пр
распределения Фишера
с (nY –1) и (nX –1)
степенями свободы
3. H1 : D( X )  D(Y )
Критическая область W – двусторонняя:
0
f1,кр
f2,кр
Пусть p( F  f1,кр )  p( F  f 2,кр )   / 2
Аналогично пунктам 1 и 2 получаем:
f 2,кр  F11 (1   / 2)
где F1(x) – функция распределения Фишера с (nX –1) и
(nY –1) степенями свободы
f1,кр
1
1

 1
f 2,кр F2 (1   / 2)
где F2(x) – функция распределения Фишера с (nY –1)
и (nX –1) степенями свободы
§ Критерий Стьюдента (t-критерий)
Генеральная совокупность распределена нормально.
Проверить гипотезу: H 0 : a  a0
a0 – некоторое число
Критерий:
xв  a
T
 n
s
Т имеет распределение Стьюдента с (n-1) степенями
свободы
Критическая область строится в зависимости от вида
конкурирующей гипотезы.
1. H1 : a  a0
Критическая область W – правосторонняя:
tпр,кр
Из требования 1 для критической области:
 p(T  tпр,кр )  
p(T  W )  
p(T  tпр,кр )  1  p(T  tпр,кр )  1  
p(T  tпр,кр )  F (tпр ,кр ) , F(x) – функция распределения T
F (tпр,кр )  1  

tпр, кр  F 1 (1   )
F(x) – функция распределения Стьюдента с (n-1)
степенями свободы
2. H1 : a  a0
Критическая область W – левосторонняя:
tлев,кр
Из требования 1 для критической области:
 p(T  t лев ,кр )  
p(T  W )  
p(T  t лев ,кр )  F (t лев ,кр )   , F(x) – функция
распределения T
 t лев , кр  F 1 ( ) , F(x) – функция распределения
Стьюдента с (n-1) степенями
свободы
Плотность распределения Стьюдента – чётная функция
f(x)
p(T<-t) -t
 p(T  t )  p(T  t )
t p(T>t)
Критическая точка tпр,кр находится из требования:
p(T  tпр,кр )  

p(T  tпр,кр )  

–tпр,кр является критической точкой для левосторонней
области:
t лев , кр  tпр , кр
3. H1 : a  a0
Критическая область W – двусторонняя:
t1,кр
Пусть
t2,кр
p(T  t1, кр )  p(T  t2, кр )   / 2
В силу чётности плотности распределения Стьюдента:
t1, кр  t2, кр
Аналогично пунктам 1 и 2 получаем:
t2, кр  F 1 (1   / 2), t1, кр  t2, кр
t1, кр
или
 F 1 ( / 2),
t2, кр  t1, кр
2. H1 : D( X )  D(Y )
Обозначим
1 sY2
F   2
F sX
H1 : D(Y )  D( X )
, F’ имеет распределение
Фишера с (nY –1) и (nX –1)
степенями свободы
 предыдущий случай:
 ,кр  F 1 (1   ), где F(x) –
f пр
0
функция распределения F’
f’пр,кр
 ,кр )  
p( F   f пр
 ,кр )  p( F  1 / f пр
 ,кр )
 ,кр )  p(1 / F  f пр
p( F   f пр

 ,кр )  
p( F  1 / f пр
Однофакторный дисперсионный анализ
Пример: выявить зависимость объёма выполненных
на стройке работ за смену от работающей бригады.
Номер бригады
Номер наблюдения
1
2
3
4
5
6
Средний объём
1
2
3
4
20
25
22
24
30
23
24
27
31
22
32
18
19
29
26
28
28
24
23
23
21
20
26
25
23
X – случайная величина
F – фактор, воздействующий на случайную величину X
F1, F2, …, Fp – уровни фактора
a1, a2, …, ap – математические ожидания на уровнях
F1, F2, …, Fp соответственно
H0: a1 = a2 = … = ap
Дисперсионным анализом называется статистический
метод, предназначенный для выявления влияния
отдельных факторов на результат эксперимента, а
также для последующего планирования эксперимента.
Критерий Бартлетта
H0: D1(X) = D2(X) = … = Dp(X)
гипотеза о равенстве дисперсий на каждом уровне
q1, q2, …, qp – количество наблюдений на уровнях
F1, F2, …, Fp соответственно
s12, s22, …, sp2 – исправленные выборочные дисперсии
на уровнях F1, F2, …, Fp соответственно
p
s02 

( qi  1) si2
i 1
p
 ( qi  1)
i 1
,




p



1
1
1


Q  1 
 p




 3( p  1)  i 1 qi  1


(
q

1
)

i




i 1



1
Критерий:
2

s
  Q    ( qi  1)  ln 02 
si 
i 1 
p
Если q1, q2, …, qp > 3, то критерий имеет распределение,
близкое к распределению Пирсона с (p-1) степенями
свободы.
Критическая область – правосторонняя.
p ( W )  p(   кр )   
F ( кр )  1  
p(   кр )  1  
p(   кр )  F ( кр )
  кр  F 1 (1   ) ,
где F(x) – функция распределения
Пирсона с (p–1) степенями свободы.
Уровень фактора F
Номер наблюдения
1
F1
F2
…
Fp
x11
x12
…
x1p
2
x21
x22
…
x2p
…
Число наблюдений
q1
q2
…
qp
Среднее значение
y1
y2
…
yp
H0: a1 = a2 = … = ap
Объём выборки: n = q1+ q2+…+ qp
Уровень фактора F
Номер наблюдения
1
F1
F2
…
Fp
x11
x12
…
x1p
2
x21
x22
…
x2p
…
Число наблюдений
q1
q2
…
qp
Среднее значение
y1
y2
…
yp
1-ая группа – уровень F1: x11, x21, … , xq11
2-ая группа – уровень F2: x21, x22, … , xq 2
2
…
p-ая группа – уровень Fp: x1p, x2p, … , xq p p
Dв= Dмежгр+Dвнгр
1-ая группа – уровень F1: x11, x21, … , xq11
2-ая группа – уровень F2: x21, x22, … , xq 2
2
…
p-ая группа – уровень Fp: x1p, x2p, … , xq p p
p
1.
Dмежгр=
2
q
(
y

x
)
i i в
i 1
n
Факторная сумма:
p
Sфакт =
2
q
(
y

x
)
i i в
i 1
p
2.
Dвнгр=
 qi Di г р
i 1
n
, где Diгр – дисперсия i–той группы
i-тая группа: x1i, x2i, … , x qii , групповая средняя: yi
qi
2
(
x

y
)
 ji i
Diгр=
qi
 qi

 ( x  y )2 / q 
q
 i   ji i i 
i 1  j 1
 

n
p
p
Dвнгр=
j 1
 qi Di г р
i 1
n
p qi
p qi
2
(
x

y
)
 ji i
i 1 j 1
Остаточная сумма: Sост =  ( x ji  yi ) 2
i 1 j 1
n
Факторная дисперсия:
Остаточная дисперсия:
2
sфакт
2
sост

Sфакт
p 1
Sост

n p
2
D( x )  sост
– всегда
2
D( x )  sфакт
– если несущественно влияние фактора
H0: a1 = a2 = … = ap
2
2
H 0 : Sост
 S факт
2
2
H 0 : Sост
 S факт
Критерий: F 
2
sфакт
2
sост
имеет распределение Фишера с
(p–1) и (n–p) степенями свободы
2
2
H1 : S факт
 Sост
Критическая область W – правосторонняя:
0
fпр,кр
Из требования 1 для критической области:
p( F W )    p( F  f пр ,кр )  

f пр ,кр  F 1 (1   )
F(x) – функция распределения Фишера с (p–1) и (n –p)
степенями свободы
Элементы теории корреляции
Зависимость величины Y от X называется функциональной, если каждому значению величины X соответствует единственное значение величины Y.
Зависимость величины Y от X называется статистической (вероятностной, стохастической),
если каждому значению величины X соответствует не
одно, а множество значений величины Y, причём
сказать заранее, какое именно значение примет
величина Y невозможно.
Среднее значение, которое принимает величина Y при
X=x, называется математическим ожиданием случайной величины Y, вычисленным при условии, что X=x,
или условным математическим ожиданием:
М(Y|X=x)
Если при изменении x условные математические
ожидания М(Y|X=x) изменяются, то говорят, что имеет
место корреляционная зависимость величины Y от X.
При этом функцию f (x)=М(Y|X=x) называют функцией
регрессии.
f (x)=М(Y|X=x) – ?
f (x)=М(Y|X=x) – ?
Условным средним y x называют среднее арифметическое наблюдавшихся значений Y, соответствующих
X=x.
Условное среднее является оценкой условного математического ожидания: М(Y|X=x)  y x
Каждому x соответствует своё значение y x , следовательно, y x – есть функция от x:
y x  f * ( x)
это уравнение называется выборочным уравнением
регрессии, а функция f*(x) – выборочной функцией
регрессии.
f ( x)  f * ( x)
f (x)=М(Y|X=x) – ?
Если функция регрессии – линейная:
f (x) = М(Y|X=x) = ax+b,
то выборочное уравнение регрессии имеет вид:
 n xy xy  nx y
Y
x, y
– выборочy x  y  rв
( x  x ) , где rв 
X
n X  Y
ный коэффициент корреляции
x, y – выборочные средние
 X , Y – выборочные средние квадратические отклонения
nxy – частота пары вариант (x, y)
Корреляционная таблица
X
10
20
30
40
nY
0.4
5
–
7
14
26
0.6
–
2
6
4
12
0.8
3
19
–
–
22
nX
8
21
13
18
n=60
Y