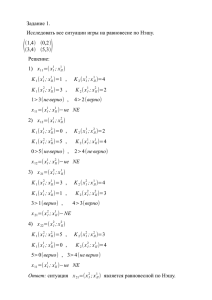J(x,y)

Бесконечные
антагонистические игры
Лектор:
доцент каф. АОИ
Салмина Нина
Юрьевна
Понятие бесконечной игры
Нормальная форма игры:
Г = <X, Y, J>
X – множество чистых стратегий 1-го игрока
Y – множество чистых стратегий 2-го игрока
J – функция выигрыша 1-го игрока
Принцип оптимальности:
max min J ( x, y)  min max J ( x, y)
xX
yY
yY
xX
Игры на единичном квадрате
Антагонистические игры, в которых оба игрока
имеют континуум чистых стратегий,
называются играми на единичном квадрате
Примеры:
Г = < [0,1], [0,1], J(x,y) >
Г = < [-2,2], [0,10], J(x,y) >
Г = < [2,4], [-1,0], J(x,y) >
Если функция выигрыша J(x,y) непрерывна по обеим
переменным, то игра имеет решение в смешанных
стратегиях
Понятие смешанной стратегии
Смешанная стратегия игрока 1 (2) есть
вероятностное распределение на множестве
2x (2y )
2x (2y ) – множество всех подмножеств X (Y)
Примеры смешанных стратегий:
1
1 

F  
,
 2 x 0 2 x 1 
1
1
1 

F  
,
,
 4 x 2 2 x 1 4 x 3 
1
1
1 

Q
,
,
3

 y 0 3 y 1 3 y  2 
1
Q
2

1
,
y[1, 2 ] 2



y  1 
Выпуклые и вогнутые функции
Функция f(x) выпукла, если
d 2 f ( x)
0
2
dx
Функция
f(x) вогнута, если
d 2 f ( x)
0
2
dx
Выпуклые и вогнутые игры
Игра на единичном квадрате называется выпуклой
(вогнутой), если J(x,y) выпукла по y (вогнута по x).
Игра на единичном квадрате вогнуто-выпукла, если ее
функция выигрыша вогнута по x при каждом значении y и
выпукла по y при каждом значении x.
В выпуклой игре у второго (минимизирующего) игрока
имеется чистая оптимальная стратегия.
В вогнутой игре у первого (максимизирующего) игрока
имеется чистая оптимальная стратегия.
В вогнуто-выпуклой игре существует седловая точка в
чистых стратегиях.
Решение вогнуто-выпуклых игр
Функция выигрыша вогнута по х
Функция выигрыша выпукла по y
Оба игрока имеют решение в чистых стратегиях
V  max min J ( x, y)  min max J ( x, y)
xX
yY
yY
(можно использовать любой критерий)
xX
Пример 1
Г  [1,1], [1,1], 3xy  x 2  2 y 2  2 y 
Проверяем игру на выпуклость/вогнутость:
J x'  3 y  2 x
J xx''  2  0 - игра вогнута
J y'  3x  4 y  2 J yy''  4  0 - игра выпукла
Выбираем минимаксный критерий: V  min max J ( x, y)
y
x
Пример 1
Г  [1,1], [1,1], 3xy  x 2  2 y 2  2 y 
Проверяем игру на выпуклость/вогнутость:
J x'  3 y  2 x
J xx''  2  0 - игра вогнута
J y'  3x  4 y  2 J yy''  4  0 - игра выпукла
Выбираем минимаксный критерий: V  min max J ( x, y)
y
x
J x'  0  x  1.5 y
J  4.5 y 2  2.25 y 2  2 y 2  2 y  4.25 y 2  2 y
J y'  0  8.5 y  2  0  y*  4 / 17  0.2353
x*  1.5 y  6 / 17  0.3529
Пример 1 (продолжение)
Г  [1,1], [1,1], 3xy  x 2  2 y 2  2 y 
J y'  3x  4 y  2 J yy''  4  0
Выбираем максиминный критерий:
V  max min J ( x, y)
x
y
J y'  0  y  0.5  0.75x
J  1.5 x  0.5  2.125 x 2
J x'  0  1.5  4.25 x  0  x*  6 / 17  0.3529
y*  0.5  0.75  6 / 17  4 / 17  0.2353
Решение вогнутых/выпуклых игр
Критерий
выпуклой / вогнутой игры:
V  min max J ( x, y)
0 y 1 0 x1
V  max min J ( x, y).
0 x1 0 y 1
Существенные стратегии игроков:
Y1  y  [0, 1] J ( x* , y )  V ,
X 1  x  [0, 1] J ( x, y  )  V

Решение
Оптимальная
чистая стратегия
Оптимальная
смешанная стратегия



выпуклой
вогнутой игры
y*
x*
F*
Q*
Теорема поиска решения в
выпуклых играх
Пусть в выпуклой игре функция выигрыша J(x,y) дифференцируема по y, а
y* — чистая оптимальная стратегия 2-го игрока. Тогда:
1) если y*=1 то среди оптимальных стратегий 1-го игрока существует чистая
существенная стратегия x1 такая, что
'
J y ( x1 ,1)  0
2)
если y*=0 то среди оптимальных стратегий 1-го игрока существует чистая
существенная стратегия х2 такая, что
'
J y ( x2 ,0)  0
3)
если 0<y*<1 то среди оптимальных смешанных стратегий 1-го игрока
существует такая, которая является смесью существенных стратегий x1, x2,
и для них выполняются неравенства J ' ( x , y*)  0, J ' ( x , y*)  0
y
1
y
2
При этом стратегии употребляются с вероятностями α и (1-α)
соответственно, где α — решение уравнения:
  J y' ( x1 , y*)  (1   )  J y' ( x2 , y*)  0
Оптимальную стратегию в этом случае будем обозначать:

F *   x ,1  
1
x2

Пример 2
Г  [0,1], [0,1], y 3  2 xy  x 2  0.5x 
Проверяем игру на выпуклость/вогнутость:
J x'  2 y  2 x  0.5 J xx''  2  0 - игра НЕ вогнута (ф.выигрыша выпукла по Х)
J y'  3 y 2  2 x J yy''  6 y  0 - игра выпукла
Выбираем минимаксный критерий: V  min max J ( x, y)
y
x
Максимум по Х достигается на одной из границ интервала [0,1], в
зависимости от Y:
Пример 2
Г  [0,1], [0,1], y 3  2 xy  x 2  0.5x 
Построим графики функций:
J (0, y )  y
3
J
1.5
J (1, y)  y  2 y  1.5
3
Используем минимаксный критерий:
V  min max J ( x, y)
y
J(1,y)
1
J(0,y)
x
0.5
V
0
y*
1
y
Пример 2
Г  [0,1], [0,1], y 3  2 xy  x 2  0.5x 
Построим графики функций:
J (0, y )  y
3
J
1.5
J (1, y)  y  2 y  1.5
3
Используем минимаксный критерий:
V  min max J ( x, y)
y
1
J(0,y)
x
y 3  y 3  2 y  1.5
2 y  1.5
3
y*   0.75
4
J(1,y)
27
V
 0.422
64
0.5
V
0
y*
1
y
Пример 2
Г  [0,1], [0,1], y 3  2 xy  x 2  0.5x 
Найдем существенные стратегии:
J ( x, y*)  V
3
3
27
3
2
   2 x   x  0.5 x 
4
64
4
x2  x  0
x1  0 x2  1
Пример 2
Г  [0,1], [0,1], y 3  2 xy  x 2  0.5x 
Найдем существенные стратегии:
J ( x, y*)  V
3
3
27
3
2
   2 x   x  0.5 x 
4
64
4
x2  x  0
x1  0 x2  1
Вероятности выбора стратегий:
2
27
3
J y' (0, y*)  3     2  0 
 1.6875
16
4
2
5
3
'
J y (1, y*)  3     2 1    0.3125
16
4
27
5
  (1   )  0
16
16

5
32
Пример 2
Г  [0,1], [0,1], y 3  2 xy  x 2  0.5x 
Решение игры:
Оптимальная стратегия 1-го игрока:
Оптимальная стратегия 2-го игрока:
Цена игры:
V
27
 0.422
64
 5
27 


F*  
,
 32 x 0 32 x 1 
y* 
3
 0.75
4
Пример 3
Г  [0,1], [0,3], xy  5x 2  5 y 2 
Проверяем игру на выпуклость/вогнутость:
J x'  y  10 x J xx''  10  0 - игра вогнута
J y'  x  10 y J yy''  10  0 - игра НЕ выпукла (ф.выигрыша вогнута по Y)
Выбираем максиминный критерий: V  max min J ( x, y)
x
y
Минимум по Y достигается на одной из границ интервала [0,3], в
зависимости от X:
Пример 3
Г  [0,1], [0,3], xy  5 x 2  5 y 2 
Построим графики функций:
J ( x,0)  5x
2
J ( x,3)  3x  5 x  45
J
0
x*
1
2
Используем максиминный критерий:
-5
J(x,0)
V  max min J ( x, y)
x
y
V
-45
-47
J(x,3)
x
Пример 3
Г  [0,1], [0,3], xy  5 x 2  5 y 2 
Построим графики функций:
J ( x,0)  5x
2
J ( x,3)  3x  5 x  45
J
0
x*
1
2
Используем максиминный критерий:
-5
J(x,0)
V  max min J ( x, y)
x
y
J x' ( x,3)  3  10 x  0
x*  0.3 V  44.55
V
-45
-47
J(x,3)
x
Пример 3
Г  [0,1], [0,3], xy  5 x 2  5 y 2 
Определим существенные стратегии:
J ( x*, y )  V
0.3 y  0.45  5 y 2  44.55
5 y 2  0.3 y  44.1  0
J
0
-5
x*
1
J(x,0)
y1  3 y2  2.94
Решение игры:
x*  0.3
y*  3
V  44.55
V
-45
-47
J(x,3)
x
Примеры простых решений
1.
Г  [3,1], [1,3],  x 2  2 y 2 
x  min
2.
y  max
 x*  0, y*  3
Г  [0,2], [0,1], x 3  2 x 2  5 y 
 x*  2, y*  1