Дидактические материалы курса Математика ставит

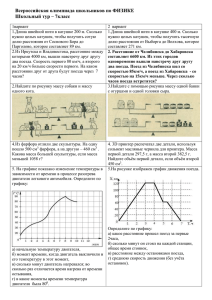
Проект «Математика ставит эксперимент»
Дидактические материалы
7-9 классы
Морохова Лариса Александровна,
учитель математики МОУСОШ № 50
г. Воронежа
Как всё начиналось ?
Чем больше становится стаж общения учащихся с
математикой, тем более абстрактными становятся в
учебнике
математические
задачи.
Ученики
сталкиваются с проблемой: «А нужна ли будет
математика в нашей дальнейшей профессии?» И
тогда мы с учениками 10 класса стали работать над
проектом «Математика ставит эксперимент»,
результатом которого стала составленная нами
книга прикладных задач по большинству тем
математики. Многие эксперименты опасно или
невыгодно проводить опытным путём. Математика
приходит на помощь и ставит свой эксперимент.
Функция
Т◦ С
1. В начале нагревания вода
имела температуру 6ºС. От
нагревания температура воды
повышалась каждую минуту на
2ºС. Составьте формулу,
которая выражает изменение
температуры Т воды от времени
t её нагревания. Будет ли эта
функция линейной? Через
сколько минут вода закипит?
О т в е т. Т = 2 t + 6, t = 47 мин.
t час
Функция
2. Годовая зарплата агронома состоит из годового
оклада и 0,3% этого оклада за каждый процент
перевыполнения плана производства
сельскохозяйственной продукции. Составьте формулу
вычисления годовой зарплаты агронома с месячным
окладом 150000 руб.
У к а з а н и е.
у = 150000 ∙ 12 + 0,003 ∙ 150000 ∙ 12х = 1800000 + 5,4х,
где х – процент перевыполнения плана производства
сельскохозяйственной продукции.
Функция
Т◦ С
3. На рисунке изображён график
изменения температуры
охлаждения смолы. Запишите
формулу зависимости между
температурой и временем.
О т в е т. T ∙ t = 50
t час
Функция
4. Участок прямоугольной формы площадью 400 м2 нужно
оградить забором. Определите размеры участка. Составьте
формулу, по которой вычисляют площадь прямоугольника.
Заполните таблицу:
Х
У
S
5
8
10
20
25
40
50
100
400 400 400 400 400 400 400 400
Постройте график, сделайте вывод. Какой из
прямоугольников вы бы выбрали для ограждения?
Почему?
Ответ
Система уравнений
5%
40%
1. Одна часть стального лома содержит 5%
никеля, а другая 40%. Сколько нужно взять лома
из каждой части, чтобы получить 140 т стали с
содержанием никеля 30%?
Р е ш е н и е. Обозначим массу первой части
лома через х, а другой – через у. Тогда
0,05 х  0,4 у  140  0,3;
 х  40,


 х  у  140,
 у  100.
Система уравнений
2. Коэффициент трения F ременных передач в
зависимости от скорости V скольжения ремня
определяют по формуле f = a + bV. Определите
постоянные a и b, если на опыте было найдено, что при
скорости скольжения V = 0,1 м/с коэффициент трения
f1 = 0, а при скорости скольжения V = 0,5 м/с – f2 = 0,5.
О т в е т.
а = 0,375, b = 0,25.
Система уравнений
3. Расстояние между двумя пристанями равно 90 км. Это
расстояние по течению реки катер проходит за 3 часа, а против
течения – за 4,5 часа. Найдите скорость катера и скорость
течения реки.
У к а з а н и е. 3v  u   90,

4,5v  u   90,
Где v - собственная скорость катера, u – скорость течения реки.
Алгебраические дроби
1. Тракторист должен вспахать участок поля за t
часов при норме а гектаров в час. За какое время
тракторист обработает этот же участок, если за
час он будет пахать на 0,1 га больше нормы?
аt
О т в е т.
.
a  0,1
Алгебраические дроби
2. Поезд мимо телеграфного столба проходит за 20 с, а
мимо моста длиной 80 м – за 25 с. Какова длина поезда?
Какова скорость поезда?
Ответ
У к а з а н и е. Когда поезд проходит мимо телеграфного
столба, то любая точка поезда на 20 с проходит расстояние х
метров, которая равна длине поезда, а когда мимо моста, то
(х+80)м за 25 с. Скорость поезда будет: х или х  80
20
25
Поскольку скорость поезда будем считать постоянной, то
х
х  80

,
20
25
Откуда х = 320 (м),
320
v
 16( м / с)  57,6(км / час)
20
Алгебраические дроби
3. Автомобиль проехал расстояние между двумя пунктами
со скоростью 75 км/час, а возвращался со скоростью 50
км/час. Какова средняя скорость его движения?
Ответ
Р е ш е н и е. Задача помогает учащимся установить разницу
ab
между средним арифметическим
и средним
2
2 ab
гармоническим
чисел а и b,
ab
c которыми часто имеют дело в курсе физики.
Обозначив расстояние между двумя пунктами через S и
искомую среднюю скорость через V, составим уравнение
2s
s
s
2 1
1

 , или 

v 75 50
v 75 50,
которое даёт возможность найти правильный ответ:
1 
 1
v  2 :     60(км / час).
 75 50 
Алгебраические дроби
4. Расстояние между двумя станциями длиной S км поезд
проходит со скоростью 60 км/час. На сколько необходимо
увеличить скорость поезда, чтобы он проходил это расстояние на
2 часа быстрее (максимальная скорость поезда на этом участке не
может превышать 100 км/час)? При каких значениях решение
возможно?
На 2 ч быстрееV
V = 60
? км/час
км/час
Р е ш е н и е. Пусть скорость поезда увеличена на
х км/час. Тогда по условию задачи имеем:
s
s
sx

 2;
 2;
60
60  x
60(60  x)
s  120 x  7200,
7200
x

.

s  120
 x  60;
По условию задачи 0  x  40, откуда
7200
7200  40( s  120)
0
 40;
 0; s  300.
s  120
s  120
Итак, задача имеет решение при условии S ≥ 300.
Неравенства
1. Диаметр шкива электродвигателя, который делает
960 оборотов в минуту, равен 150 мм. На сколько
миллиметров должен быть меньше диаметр нового
шкива, чтобы электродвигатель делал не менее чем
1200 оборотов в минуту?
У к а з а н и е. Если диаметр шкива уменьшится на х
мм, то задача сводится к решению неравенства
150  960  (150  х)   1200, откуда __ х  30см.
Неравенства
2. Машина стоимостью 4000 руб.(цены относительные)
поставлена на капитальный ремонт после 10 лет
эксплуатации. Стоимость ремонта 1600 руб. Каким должен
быть срок гарантии работы машины после ремонта, чтобы
была оправдана его стоимость.
У к а з а н и е. Обозначив через х гарантийный срок
работы машины, получим неравенство
4000 1600

, откуда    х  4( лет).
10
х
Неравенства
3. В грузовом автомобиле с двумя колёсами спереди и
четырьмя сзади шины передних колёс стираются через
20000 км пройденного пути, а задних – через 30000 км.
Сколько километров можно проехать на тех же шинах, если
их своевременно поменять местами?
Р е ш е н и е. Количество резины, которое стирается на одной
шине, пока она пригодна, возьмём за единицу. Тогда перед
началом эксплуатации автомобиля есть 6 единиц резины.
Если шина стоит на переднем колесе, то на 1 км пути
1
1
стирается 20000 единицы, если на заднем единицы.
30000
Итак на 1 км пути стирается
7х
.
единицы резины, а за х километров пути 
1
1
1
2
7
2
 400 


20000
30000
10000 15000 30000
30000
Поскольку в автомобиле может стереться не более 6 единиц
7х
2

6
,
х

25714
.
резины, то имеем неравенство 30000
7
2
25714 км ,
Шины сотрутся одновременно на пути
если каждая
7
из них пройдёт 1/3 пути на переднем колесе.
На тех же шинах можно проехать приблизительно 25700 км.
Уравнения с модулем вида
а kx  l  b  0
1. По дороге в противоположных направлениях едут
два автомобиля со скоростями 70 и 80 км/час. Через
какое время расстояние между ними будет равно 15
км, если в данный момент оно составляет S км?
У к а з а н и е. Если расстояние между автомобилями
S км, а через t часов 15 км, то по условию задачи
|S – 150 t| = 15. Если 150 t ≤ S, то S – 150 t = 15 и
S  15
если
t
, S  15
150
S  15
S  150t , тоS  150t  15иt 
, S  15
150
15км
Sкм
Sкм
15км
Квадратные уравнения.
1. Для сооружения склада вместимостью 240 м3
подготовлен материал для внешних стен общей
длиной 32 м и высотой 4 м. Какие размеры должен
иметь склад?
У к а з а н и е. Задача сводится к решению уравнения:
4х(16 – х) = 240, где х – один из размеров
прямоугольного здания.
Квадратные уравнения.
2. Для раствора, который содержит 6 кг соли, долили
100 кг воды, после чего концентрация раствора
уменьшилась на 25%. Сколько воды в растворе?
У к а з а н и е. Массу воды, которая содержится в
растворе обозначим через х. Решение задачи сводится к
нахождению корней уравнения
6  100 6  100

 25.
6  х 100  х
Квадратные уравнения.
3. Зависимость между площадью использованной
земли и валовым доходом из расчёта на 100 га
сельскохозяйственных угодий лесостепной полосы
можно выразить функцией
у ≈ 9 + 9х – 1,5х2, где х – площадь
сельскохозяйственных угодий (в тыс. га), у – валовой
доход на 100 га сельскохозяйственных угодий (в тыс.
руб). С какой площади хозяйство будет иметь
наибольшую прибыль?
У к а з а н и е. Хозяйство будет иметь наибольшую
прибыль на 100 га с площади 3 тыс. га, поскольку
у ≈ 9+9х-1,5х2=-1,5(х-3)2+22,5 = 22,5-1,5(х-3)2 ≤ 22,5.
V. Прогрессии
1. Ступенчатый шкив
состоит из 10 ступеней.
Диаметры их образуют
арифметическую
прогрессию. Наибольший
диаметр 300 мм,
наименьший - 210 мм.
Найдите другие диаметры.
О т в е т. 220, 230, …,
290.
V. Прогрессии
Задача 2. Найдите силу F,
которую необходимо приложить
к свободному концу жгутового
каната, чтобы удержать груз Р =
4  103 Н при помощи
полиспаста, который состоит из
четырёх блоков. Известно, что
благодаря трению натяжение
каната полиспаста изменяется в
геометрической прогрессии,
знаменатель которой q = 0,837.
О т в е т. F = 1530 Н.
полиспаст
Список литературы
1. Апанасов П.Т. Методика решения задач с
экономическим содержанием. – М.: Высшая школа,
1981.
2. Возняк Г.М. Взаимосвязь теории с практикой в процессе
изучения математики. – К.: Радянська школа, 1989.
3. Энциклопедический словарь юного математика/Сост.
Савин А.П. – М.: Педагогика, 1985.
Электронные издания
1. Большая Российская энциклопедия. - © «Кирилл и
Мефодий», 2002.
2. Коллекция 80000 анимаций. - www.animashky.ru