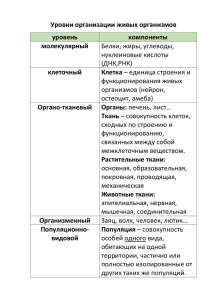
Модель передачи информации в условиях конкуренции.

Модель передачи
информации
в условиях конкуренции
Рассмотрим модель передачи информации в популяции ограниченной численности.
Список переменных и коэффициентов:
y – численность носителей информации,
x – численность необученных особей,
a – коэффициент размножения необученных особей при отсутствии лимитирующих факторов,
r – коэффициент рождаемости,
s – коэффициент смертности,
b – коэффициент взаимной конкуренции между необученными особями, а
так же
коэффициент конкурентного противостояния необученных особей по отношению к
обученным,
k
–
коэффициент взаимной конкуренции между обученными, а
так же коэффициент
конкурентного противостояния обученных особей по отношению к необученным,
c – коэффициент обучения (передачи информации от обученных к необученным).
Математическое моделирование
процессов отбора
2
Гипотезы:

Смертность и рождаемость у обученных особей равна смертности и рождаемости у
необученных , но потомство обученных всегда является необученным;

острота конкурентно противостояния обученных особей по отношению к необученным
снижена (коэффициент конкуренции
условиях противостояния
обучение
k – меньше при этом коэффициента b), так как в
невозможно,
коэффициент конкуренции
между
носителями информации так же снижен до значения k, так как приобретенная информация
способствует их консолидации;

все коэффициенты считаются положительными, k < b, c > b.
Уравнения динамики:
x  ax  cxy  bx 2  ry  kxy,
y   sy  cxy  bxy  ky .
2
Математическое моделирование
процессов отбора
(1)
3
Обозначим
w = x + y.
Уравнение динамики общей численности популяции:
  aw  bxw  kyw  w(a  (b  k ) x  kw).
w
( 2)
Нормирующая замена:
x
 
w
удельный вес необученных особей;
y
 
w
удельный вес обученных особей.
Система динамики удельных весов обученных и необученных особей:
  a  c  b 2 w  r  kw   (a  bw  r  s  kw) 
 cw  r ,
  cw  r   (cx  r ),
Математическое моделирование
процессов отбора
(3)
4
a
r a br
(
0
,
0
),
(
,
0
),
(
,  ).
Состояний равновесия:
b
c k kc
Линеаризованная система (1) в состоянии (0,0) :
x  ax  ry ,
y   sy.
Собственные числа:
1  a,
2   s.
Следовательно, (0,0) – седло.
Линеаризованная система (1) в состоянии
x  ax  ( r 
y  (
(c  k ) a
) y,
b
(
a
,0 ) :
b
ca
 r ) y.
b
Собственные числа:
1  a,
2 
ca
 r.
b
.
Математическое моделирование
процессов отбора
5
a
a
r
( ,0)  при
 седло, иначе, устойчивый узел.
b
b
c
r a
br
(
,

):
Линеаризованная система (1) в состоянии
c k
kc
ac
kr
x  
x
y,
k
c
br
  (a 
y
) y.
c
Следовательно,
Собственные числа:
ac
,
k
br
2   a  .
c
r a
br
a
r

)  при

Следовательно, ( ,
c k
kc
b
c
1  
устойчивый узел, иначе, не существует.
Математическое моделирование
процессов отбора
6
Рассмотрим вспомогательную систему:
  aw  bw 2  kw 2 ,
w
  cw  r.
Учитывая
  1   , получаем:
w  aw  bw 2  k (1   ) w 2 ,
  c (1   )w  r (1   ).
Векторное поле для этой системы:
dw aw  bw 2  k (1   )w 2 w(a  bw  k (1   )w)


d  c (1   )w  r (1   )
(1   )(cw  r )
Математическое моделирование
процессов отбора
7
Главными изоклинами являются:
 :
w
1    0,
 сw  r  0;
0 :
(1,
w  0,
a
)
b
a  bw  k (1   ) w  0.
(0,0)
1
Инвариантные прямые

w  0,   0.
Математическое моделирование
процессов отбора
8
Из плоскости
( , w) прейдем в плоскость (x, y):
y
a br

k
kc
(0,0)
r
c
a
b
x
Фазовый портрет системы (1) при ac > rb
Математическое моделирование
процессов отбора
9
y
(0,0)
a
( ,0 )
b
x
Фазовый портрет системы (1) при ac < rb
Математическое моделирование
процессов отбора
10
Рассмотрим модель, в которой существуют особи, обладающие разными видами информации.
Список переменных и коэффициентов:
x – численность необученных особей,
y – численность носителей информации первого вида,
z – численность носителей информации первого вида,
a – коэффициент размножения необученных особей при отсутствии лимитирующих факторов,
r – коэффициент рождаемости,
s – коэффициент смертности,
c – коэффициент обучения (передачи информации от обученных к необученным).
Математическое моделирование
процессов отбора
11
Гипотезы:

потомство носителей информации является необученным;

предположим, что рождаемость, смертность и эффективность передачи информации для
всех особей одинаковы;

информация от носителя одного вида не передается носителю другого вида;

коэффициент конкуренции b у носителей второго вида такой же как и у необученных
особей, а у носителей первого вида снижен до k.
Уравнения динамики:
x  ax  cy  bx 2  ry  kxy  bxz  cxz  rz ,
y   sy  cxy  bxy  ky 2  byz ,
( 4)
z   sz  cxz  bxz  bz 2  byz.
Математическое моделирование
процессов отбора
12
Обозначим w = x + y + z .
Нормирующая замена:
x
 ,
w
y
 ,
w
z
 .
w
Уравнения (4) принимают вид:
  (r  cw)(   )  kw   (k (   ) w  bw),
  r  cw  k 2 w   (k (   ) w  bw),
  r  cw  bw   (k (   ) w  bw).
Система на стандартном симплексе, представленная через функции перехода:
   r (   )  c (   ) w  kw,
  r  cw  k 2 w,
   r  cw  bw.
Математическое моделирование
процессов отбора
13




r

c

w

k

w
 r  cw  bw.
Сравним
и
 




.
Так как k < b, то


Следовательно  (t )  0 при t  , (0)  0.
Поскольку w – величина ограниченная, то z (t )  0 при t  , y (0)  0.
Линеаризованная система (4) в состоянии
(
r a
br
, 
,0) :
c k
kc
br
br

,
c
c
a br
br
a br
  (c  b)( 
)  (  a 
)  b( 
) ,
k kc
c
k kc
b a br
  (1  )( 
) .
k k kc
  
Собственные числа:
1  
br
,
c
br
,
c
b
br
3  (1  )( a 
)
k
c
2   a 
Математическое моделирование
процессов отбора
14
Таким образом,
(
r a
br
, 
,0)  при
c k
kc
a
r

устойчиво, иначе не существует.
b
c
Следовательно, общая численность популяции, как и в предыдущей модели, при
a
r

b
c
стремится к
a (b  k ) r
a br

, y(t) стремится к

,
k
kc
k kc
x(t) стремится к
r
.
c
Выводы:

существование системы носителей информации напрямую зависит от коэффициента
передачи: с ростом эффективности передачи увеличивается удельный вес носителей
информации;

для передачи информации большое значение имеет внутренняя конкуренция – уровень
противостояния между актуальными и потенциальными носителями информации. Чем
ниже уровень этого противостояния, тем легче передается информация.
Математическое моделирование
процессов отбора
15