Методы экспериментальной оптимизации

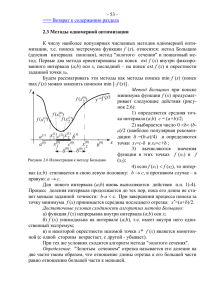
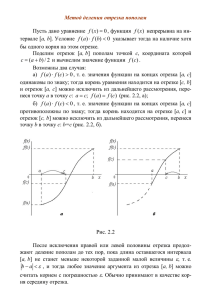
МЕТОДЫ
ЭКСПЕРИМЕНТАЛЬНОЙ
ОПТИМИЗАЦИИ
Метод деления отрезка пополам
Метод позволяет исключать на каждой итерации в точности половину интервала.
Иногда этот метод называют трехточечным поиском на равных интервалах,
поскольку его реализация основана на выборе трех пробных точек, равномерно
распределенных в интервале поиска.
Шаг 1. Положить xm=(a+b)/2 и L=b-a. Вычислить значение I(xm)
Шаг 2. Положить x1=a+L/4 и x2= b-L/4. Точки x1,xm,x2 делят отрезок [a,b] на четыре
равные части. Вычислить значения I(x1) и I(x2).
Шаг 3. Сравнить I(x1) и I(xm). Если I(x1) < I(xm), исключить интервал (xm,b] , положив
b=xm. Средней точкой нового интервала поиска становится точка x1. xm=x1.
Перейти к шагу 5. Если I(x1) ≥ I(xm), перейти к шагу 4.
Шаг 4. Сравнить I(x2) и I(xm). Если I(x2) < I(xm), исключить интервал [a,xm), положив
a=xm. Так как средней точкой нового интервала становится точка x2, положить
xm=x2. Перейти к шагу 5. Если I(x2) ≥ I(xm), то исключить интервалы [a, x1) и (x2,b] и
положить a = x1 и b = x2. Перейти к шагу 5.
Шаг 5. L=b-a. Если величина |L| мала, закончить поиск. В противном случае
вернуться к шагу 2.
Метод деления отрезка пополам
I ( x)
a
I ( x)
а
x
1
x
m
x
x
2
b
a
I ( x)
б
x
1
xm
x
2
b
x
a
в
x
1
x
m
x
x
2
b
Особенности метода:
1. На каждой итерации алгоритма исключается в точности половина интервала
поиска.
2. Средняя точка последовательно получаемых интервалов всегда совпадает с
одной из пробных точек x1, x2 или xm, найденных на предыдущей итерации.
Следовательно, на каждой итерации требуется не более двух вычислений значения
функции.
3. Если проведено n вычислений значения функции, то длина полученного интервала
составляет (1/2)n/2 величины исходного интервала.
4. В литературе показано, что из всех методов поиска на равных интервалах
(двухточечный, трехточечный, четырехточечный и т. д.) трехточечный поиск, или метод
деления интервала пополам, отличается наибольшей эффективностью.
Метод золотого сечения
Золотым сечением отрезка называют деление его на две неравные части так, что
отношение длины всего отрезка к длине большей части равно отношению длины
большей части к длине меньшей части отрезка.
Точки x1 и x2 осуществляют золотое сечение
отрезка [a,b].
3 5
x a
(b  a )  a  0.381966  (b  a )
2
1
x2  a 
5 1
(b  a )  a  0.618033 (b  a )
2
Оказывается, что точка осуществляет золотое
сечение отрезка [a,x2] , а точка x2 – отрезка [x1,b].
Этот факт позволяет на каждой итерации (за
исключением первой) добавлять только по одной
экспериментальной точке (с учетом золотого сечения).
x1
1 
a
1


x1


b
; 1    2
1 
5 1

 0.61803...
2
1 

x2
b
x1 x 2
b
a

1 
a
2
Метод золотого сечения
Итерационная процедура сокращения отрезка [a,b] выглядит следующим образом.
Точки x1 и x2 золотого сечения вычисляется
минимизируемая функция I(x1) и I(x2).
Если I(x1)≤I(x2), то принимается a1=a, b1=x2, x2=x1.
Если I(x1)>I(x2), то принимается a1=x1, b1=b, x2=x2.
Отрезок [a1, b1] содержит x0.
На n-m шаге после вычисления I(x1), I(x2), I(xn+1) найден отрезок Отрезок [an, bn]
включающий x0.
По заданной величине δ точности поиска x0 необходимое число шагов n вычисляется
из равенства:
[( 5  1) / 2]n (b  a )  
Метод с использованием квадратичной
аппроксимации
При реализации метода оценивания функции I(x) с использованием квадратичной
аппроксимации предполагается, что на ограниченном интервале можно
аппроксимировать функцию квадратичным полиномом, а затем использовать
аппроксимирующую функцию для оценивания координаты точки истинного минимума
функции I(x).
Если задана последовательность точек x1, x2, x3 из интервала [a,b] и известны значения
функции I(x1), I(x2), I(x3) , то можно определить три коэффициента a0, a1, a2 из условия,
что значения квадратичной функции
q( x)  a0  a1 ( x  x1 )  a2 ( x  x1 )( x  x 2 )
Находим коэффициенты:
a0  I 1
a1  ( I 2  I 1 ) / ( x 2  x1 )
 I 3  I1 I 2  I1 
 I 3  I1

1




a2  3


a
1
2  3
1
2
1
3
2  3
1
(x  x )  x  x
x  x  (x  x )  x  x

1
Находим точку x0, обеспечивающую минимум квадратичной аппроксимации:
dq
 a1  a2 ( x  x 2 )  a2 ( x  x 1 )  0
dx
x 0  ( x1  x 2 ) / 2  (a1 / 2a2 )
Одномерный глобальный поиск
Наиболее эффективные и теоретически обоснованные алгоритмы глобальной
аппроксимации трудны для реализации. Поэтому чаще реализуют более простые
алгоритмы, отвечающие частным критериям рациональности.
Считаем, что минимизируемая функция I(x), a ≤x ≤b – липшицева функция с известной
константой L.
| I ( x2 )  I ( x1 ) |  L | x2  x1 |
 L | x  x i | I ( x)  I ( x i )  L | x  x i |, x, x i [a, b]
i ( x )  I ( x i )  L | x  x i | I ( x )
I ( x)
I ( x)
I ( x )  I ( x i )  L| x  x i |
I
a
x
xi
i
i
i
I ( x )  L | x  x |  ( x)
b
x
a
x3
x1
x5
[a , b] \ D 
x4
b
x2
x
Последовательный симплексный метод
Правильный симплекс – это регулярный многогранник.
Шаг 1. Задается исходная вершина
симплекса, размер симплекса и строится
симплекс.
Шаг 2. В вершинах симплекса
вычисляется минимизируемая функция.
Шаг 3. Осуществляется проверка
выполнения условий окончания поиска
оптимума.
Шаг 4. Находится наихудшая вершина симплекса. Эта вершина с максимальным
значением. Производится отражение симплекса.
Шаг 6. Если новый симплекс хуже предыдущего, то возврат к предыдущему симплексу
и его редукция. Переход на Шаг 3.
Метод деформируемого многогранника
В целях ускорения сходимости, повышения точности при подходе к экстремуму и
устранения трудностей на искривленных оврагах симплексный метод был
модифицирован Нелдером и Мидом.
Правильный симплекс в процессе поиска меняет свою форму и становится
неправильным, а добавление к нему дополнительных точек трансформирует его в
деформируемый многогранник. Деформируемый многогранник (даже деформируемый
симплекс) по сравнению с правильным симплексом адаптируется к топографии
целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, меняя
направление в изогнутых впадинах и сжимаясь в окрестности минимума.
Метод деформируемого многогранника
 1
а
xm4
xm3
б
0   1
xp
xp
в
г
0   1
x p  1
0
 1
xm2
xm2
xm2
xm3   1.5
xi
xi
= 3
xl
Процедура отыскания вершины с
меньшим значением I(x) состоит из
следующих операций:
а) Отражение.
б) Растяжение.
в) Сжатие.
г) Редукция.
Эти операции позволяют значительно
ускорить сходимость симплекс метода.
Градиентный метод с использованием
планирования первого и второго порядка
x2
x2

x2l

x1l
x1


x1
Методы случайного поиска
Наиболее простой способ использования случайности при поиске минимума
функции заключается в следующем. Внутри области, где отыскивается экстремум,
последовательно по случайному механизму распределяются точки x и в них
измеряется функция качества. Точки, обеспечивающие наименьшее значение
функции качества, запоминаются. Процесс поиска заканчивается, когда число
безрезультатных проб превысит порог.
Проба считается безрезультатной, если значение функции качества больше, чем
наименьшее значение функции, встретившееся во всех предыдущих пробах.
Недостатком данного способа поиска экстремума является чрезвычайно большое
число испытаний.
Рассмотрим еще один способ: сочетание локальных детерминированных методов
поиска со случайным просмотром области. Производится n запусков алгоритмов
локального поиска из случайных точек. Среди них отбирается самая минимальная и
считается оценкой глобального минимума.