Решение задач векторно

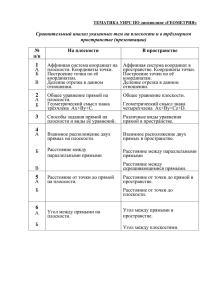
Система работы учителя
математики по подготовке
учащихся к ЕГЭ
Что я считаю самым важным при подготовке к ЕГЭ?
1.Вычислительные навыки.
2.Обязательное знание правил и
формул.
3.Постоянное совершенствование
учебных навыков на практике.
4.Проверка знаний и умений
учащихся.
Информационная поддержка
участника ЕГЭ




www.educom.ru – сайт Департамента образования
www.fipi.ru – сайт Федерального института
педагогических измерений – здесь указана
рекомендуемая литература по отдельным
предметам
www.ege.edu.ru – портал поддержки ЕГЭ, где
размещена вся основная информация о ЕГЭ
www.mioo.ru – сайт Московского института
открытого образования, где действует система
прямых ссылок на наиболее важные страницы
портала поддержки
Этапы совместной работы учителя и
родителей
1. информационный этап;
- рекомендации ученику;
- рекомендации родителям;
2. систематическая связь с
родителями.
Рекомендации ученику
ПОМНИТЕ! Фундамент математических знаний закладывается на
обычных уроках математики и при систематической подготовке к
ним.

Необходимо внимательно выслушивать теоретический материал
на уроках.

Старайтесь не пропускать без уважительной причины уроки
математики.

Не допускайте формального усвоения программного материала.

Помните, что умение решать задачи является следствием глубоко
понятого соответствующего теоретического материала.

Выполняйте все домашние задания самостоятельно, и
своевременно выясняйте непонятные моменты.

Составьте свой личный план подготовки к экзамену. Покажите его
учителю или другому квалифицированному специалисту для
подтверждения его правильности и соответствия вашим
индивидуальным способностям.

Регулярно занимайтесь дополнительно по личному плану, не реже
1 раза в неделю.

Запомните: вся подготовка к экзамену зависит лично от каждого
из вас.

Роль учителя в школе действительно велика, но он не всемогущ, и
обучить может лишь того, кто хочет учиться и кто сам учится.
Рекомендации родителям
Уважаемые папы и мамы!





Неверно думать, что если у Вас нет
математического образования, то Вы ничем не
можете помочь своему ребенку при подготовке к
ЕГЭ.
Это всегда можно сделать, организуя и
контролируя его самоподготовку. Здесь Ваша
помощь просто необходима.
Ознакомьтесь с « Рекомендациями ученику» и
помогайте ребенку их выполнять.
Контролируйте его работу и посещаемость на
уроках математики в школе (не реже 1 раза в месяц
встречайтесь с учителем математики и старайтесь
выполнять его рекомендации).
Организуйте качественное питание и отдых
ребенка в течение всего учебного года (особенно в
период сдачи экзаменов).
Рекомендации учителю







Материал на уроках необходимо излагать в простой,
доступной, понятной форме.
Формы работы на уроках необходимо разнообразить,
повышая тем самым интерес к предмету.
Необходимо добиваться от учащихся не формального
усвоения программного материала, а глубокого
осознанного его понимания.
В процессе преподавания необходимо делать
определенные акценты на те разделы, которые
представлены в тестах ЕГЭ.
Объяснение нового материала необходимо строить
как можно более наглядно, создавать яркие образы.
Необходимо разработать систему контроля знаний
учеников и возможность устранения пробелов в их
знаниях.
Необходимо сформировать у всех учащихся
достаточно высокий уровень учебной самостоятельной
деятельности,
Полезные замечания:
1.
2.
3.
4.
5.
Любую задачу С2 можно решить методом
координат.
Метод координат – не единственный метод
решения задач С2
Метод координат универсален, потому что
есть алгоритм решения для любого типа
заданий С2.
Целесообразно задавать систему координат
специальным способом для разных
объектов.
Целесообразно изображать плоскость Оху и
основание геометрического тела в ней
отдельно.
Общий алгоритм для решения С2
методом координат
1. Ввести прямоугольную систему координат (выбор
зависит от объекта).
2. Выписать координаты всех необходимых точек.
3. Вычислить координаты необходимых векторов.
4. Применить формулу, выполнить вычисления.
5. Записать ответ.
Примеры «удобного» задания системы координат для разных
объектов
Прямоугольный параллелепипед
z
y
y
х
х
Правильная треугольная призма
z
y
1
3
2
1
2
y
х
х
Правильная шестиугольная призма
y
1
2
1
3
2
х
Правильная пирамида
1. Начало координат в центре описанной
(вписанной) около основания окружности
2. Ось Оz – проходит по высоте пирамиды
z
О
1
2
А
y
3
2
1
y
х
Задача 1 (угол между прямыми)
В правильной шестиугольной призме А…F1,
все ребра которой раны 1, найдите
косинус угла между прямыми АВ1 и ВС1
1/2
3
2
1
Решение
задачи
1
Введем прямоугольную систему координат
z
(см. рисунок)
А(0;0;0)
1/2
В(0;1;0)
В1 (0;1;1)
3 3
С1 (
; ;1)
2 2
АВ10;1;1
 3 1 
ВС1 
; ;1
 2 2 
3
2
1
y
x
cos  
3 1
0  ( )   1
2
2
3 1
0 11
 1
4 4
Ответ: 0,75
у
х
3
3
2


2 2 4
Задача 2 (угол между прямой и
плоскостью).
В кубе A...D1 найдите тангенс угла между прямой AC1 и
z
плоскостью BDD1.
В
С
y
А
D
х
х
ÀÑ  DB (äèàãîíàëè êâàäðàòà )
ÀÑ  ÂÂ1 ( ò .ê .ÂÂ  ( ÀÂÑ ))
çíà÷èò , ÀÑ  ( ÂÂ1 D1 )( ïðèçíàê ïåðïåíä . ïðÿìîé
è ïëîñêîñòè
)
у
Решение задачи 2
z
Введем прямоугольную систему координат
(см. рисунок)
В
С
y
А
D
ÀÑ 1;1;0
у
х
Пусть α – искомый угол)
ÀÑ1 1;1;1
х
А(1;0;0)
С(0;1;0)
С1(0;1;1)
11 0
2
sin   cos( ÀÑ; ÀÑ1 ) 

11 0 111
6
4
1
соs  1  
6
3
tg  2
Ответ : 2
Задача 3.Угол между
плоскостями
В правильной четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите косинус двугранного угла, образованного гранями
SBC и SCD.
z
D
С
y
А
В
О
х
х
Введем прямоугольную систему координат (см.рис.)
Найдем угол между перпендикулярами к плоскостям SBC и SCD.
Обозначим искомый угол α.
Составим уравнения плоскостей.
у
Решение задачи 3
(1) aх+by+cz+d=0 – общий вид уравнения плоскости
вектор _ na; b; c  плоскости
z
Т.к. точки S,B,C принадлежат плоскости SBC,
то их координаты удовлетворяют уравнению (1)
Составим и решим систему уравнений
1 1 
В ; ;0 
2 2 
 1 1 
С   ; ;0 
 2 2 

2

S  0;0;
2 

1
1
 2 a  2 b  d  0;

1
 1
 a  b  d  0;
2
 2
 2
cd 0

 2
х
у
Неизвестных 4, уравнений 3
Пусть d=1
Решение задачи
3(продолжение)
a  0;
b  2;


c   2 ;
 d  1.

Аналогично найдем координаты вектора,
перпендикулярного плоскости SCD

2


S  0;0;
2 

 1 1 
C   ; ;0 
 2 2 
 1 1 
D  ; ;0 
 2 2 


m2;0; 2  SCD
n 0;2; 2  SBC
cos  
Ответ :
1
3
002
42 42

1
3
z
у
х
 2
с  d  0;

 2
1
 1
 a  b  d  0;
2
 2
1
 1
 2 a  2 b  d  0.

a  2;
b  0;


c   2 ;
 d  1.

Задача 4 (Расстояние от точки до
прямой)
В правильной шестиугольной пирамиде SABCDEF, стороны основания
которой равны 1, а боковые ребра равны 2, найдите расстояние от точки F до
Прямой BG, где G – середина ребра SC
z
SO  4  1  3
FBG
S (0;0; 3 )
C (0;1;0)
FB 
 1 3

G  0; ;

 2 2 
F (0;1;0)
 3 1 
B
; ;0 
 2 2 
3 9
 0  3
4 4
FG  0 
BG 
9 3
  3
4 4
3
3
6
0 
4
4
2
х
у
BFG  равнобедренный
6
21
42
FH  3 


16
8
4
42
Ответ :
4
Задача 5 (Расстояние от точки до плоскости)
В единичном кубе А…D1 найдите расстояние от точки А до плоскости ВDA1
Решение:
Введем прямоугольную систему координат
А1 (1;0;1)
D (0;0;0)
B (1;1;0)
А(1;0;0)
a  1
b  1


c  1
d  0
z
а  с  d  0

d  0
a  b  d  0

у
х
1
3


3
111
3
Ответ :
3
Задача 6 (Расстояние от точки до плоскости)
В правильной шестиугольной пирамиде SABCDEF, стороны основания
которой равны 1, а боковые ребра равны 2, найдите расстояние от точки А до
плоскости SBC.
z
Уравнение _ плоскости
3 1
A( ; ;0)
2
2
3 1
B ( ; ;0)
2 2
C (0;1;0)
SBC :
 3c  d  0

1
 3
a

bd 0

2
 2
b  d  0
SO  4  1  3 
S (0;0; 3 )
a  3

b  3

c  3
 d  3


O
у
х
3
 1
3
 3    3
2
 2
393
3
15


5
15
Ответ :
15
5
Задача 6 (Расстояние между скрещивающим
прямыми)
В единичном кубе А…D1 найдите расстояние от АD1 до A1C1
Пусть NM- общий перпендикуляр прямых АD1 и A1C1
z
NM  x AD1  AA1  y A1C1
AD10;1;1
A1C1 1;1;0
2 x  y  1

2 y  x  0
2

x


3

y  1

3
 1 1 1
NM  ; ; 
 3 3 3
NM  AD1  0
NM  A1C1  0
АА10;0;1
NM  y; x  y; x  1
x  y  x  1  0

y  x  y  0
у
х
A
N
Ответ : NM 
3
3
A1
M
Разные задачи С2
Задача № 1
Так как косинус угла между прямыми равен модулю косинуса угла
между направляющими векторами, то косинус угла между АЕ и ВК
равен 2
5
Задача № 2
Задача № 3
Задача № 4
Задача № 5
Задача № 6
Задача № 7
Тренировочная работа Угол между прямыми
Тренировочная работа
Угол между прямой и плоскость
Тренировочная работа
Угол между двумя плоскостями
Тренировочная работа
Расстояние от точки до прямой
Тренировочная работа
Расстояние от точки до плоскости
Тренировочная работа
Расстояние между двумя прямыми
Диагностическая работа
Ответы к диагностической
работе