20 км/ч

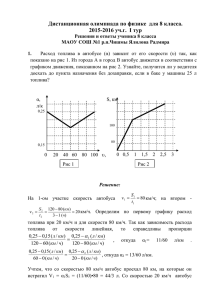
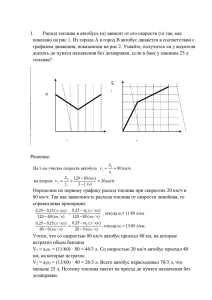
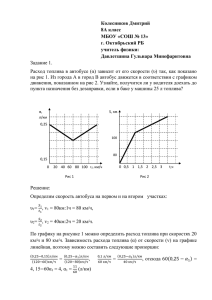
1. Решение: По графику ( рис1) на первом участке скорость автобуса
v1=
V1=
80 км
1ч
𝑠1
𝑡1
= 80км/ч;
На втором участке v2 =
V2 =
120 км−80км
3ч−1ч
𝑠2
𝑡2
= 20 км/ч
По графику (рис 1) расход топлива определим при 20 км/ч и при 80 км/ч.
Так как ∝ (𝑣) линейная функция, то
11
∝1=
60
л
км
км
120 − 60 км/ч
ч
0,25 − 0,15 л/км
=
л
км
км
120 − 80 км/ч
ч
0,25 − ∝1 л/км
л/км
л
км
км
60 − 0 км/ч
ч
0,25 − 0,15 л/км
=
л
км
км
20 − 0 км/ч
ч
0,25 − ∝2л/км
; ∝2 =
13
60
л/км
Со скоростью V1 = 80км/ч автобус проехал 80 км и истратил V1 = ∝ 𝟏*S1
V1 =
11
60
*80 =
44
3
2
= 14 (л);
3
Со скоростью 20 км/ч проехал 40 км и истратил V2 = ∝ 𝟐*S2;
V2=
13
26
60
3
*40 =
2
= 8 (л).
3
2
2
1
3
3
3
Всего V1+ V2= 14 + 8 = 23 (л)
1
23 (л) < 25 л, значит, топлива хватит.
3
Ответ: топлива хватит, чтобы добраться из пункта А до В
2.
Решение: расставим силы, действующие на шар, когда шар летит вверх и
вниз.
F сопр.1 = F сопр; F сопр.2 =
𝐹сопр
2
так как F сопр2~v( после
освобождения балласта стал подниматься вдвое меньшей скоростью)
Fсопр + F арх. = m1g
𝐹сопр
2
+ m2g = Fарх.
Fсопр +
3
2
3
2
3
2
𝐹сопр
2
+ m2g=
Fсопр = m1g
- m2g
Fсопр =g(m1-m2)
Fсопр = g*60
m1g
Fсопр = 400H
Ответ: 400Н.
3. Решение:
Представим стержень как две материальные точки массами m и m.
Тогда получится рычаг, на плечи которого действует равные силы.
Тогда и плечи сил равны,
𝑙
2
-x=x
2x =
X=
𝑙
4
1м
4
= 0.25 м.
Ответ: прут надо подвесить на расстоянии 0.25 м от вершины
прямого угла.
4. Решение:
При нагреве энергетический баланс Q=N𝜏1=cm∆𝑡 1+Nпотерь 𝜏1 (1).После
отключения кипятильника сm ∆𝑡2 = 𝑁потерь 𝜏2, (2)где N-мощность
нагревателя, m-масса воды в кастрюле, 𝜏1 и 𝜏2- это время нагрева и
охлаждения
𝑁𝜏1−ст ∆𝑡1
Из (1):N потер
𝜏1
Из (2) Nпотерь
с𝑚∆𝑡2
𝜏2
𝑁𝜏1 − ст𝑚∆𝑡1 с𝑚∆𝑡2
=
𝜏1
𝜏2
(N𝜏1-сm∆t1)*𝜏2= сm∆𝑡2 ∗ 𝜏1 ∗ 𝑁𝜏1 ∗ 𝜏2 − с𝑚∆𝑡1 ∗ 𝜏2 = с𝑚∆𝑡2 ∗ 𝜏1
M=
𝑁 𝜏1
𝜏1
𝑐(∆𝑡1+ ∆𝑡2)
𝜏2
=
500вт∗1с
Дж
4200
кг кг с∗(5 с+120с∗1 с)
60с
=
60000
29400
≈ 2 кг
Ответ:2 кг
5. Решение:
Вытопленная вода имеет массу m=𝜌(𝐻2𝑂)*V масса содержимого котелка и
масса снега не изменилась. mснега = mводы; 𝜌снега* V кот =
𝜌(𝐻2𝑂)*Vводы
𝑚
𝜌(𝐻2𝑂)∗𝑉
𝜌𝑐
𝜌𝑐н
Тогда V кот = =
=
𝜌(𝐻2𝑂)
𝜌 снега
∗ 𝑉 = 4 ∗ 0.75 == 3л
Ответ: 3л
6. Решение: V «гриба» = l*s= 0.01м*0,01м2 = 0,0001м3
2) 100м2 - 100%
х – 5%
х = 5м2 - покрыта «грибами»
5: 0,01 = 500(ледяных грибов)
𝐴 𝑄 𝑄1+𝑄2+𝑄3
3) P= = =
𝑡
𝑡
𝑡
Q1=C льда*m льда*(t2-t1)
кг
Q2= λ льда*m льда; m=𝜌 ∗ 𝑉 = 900 3 *0,001м3
м
Q3=C льда*m воды*(t3 – t2)
Q1=2100
ДЖ кг
* *0,0001м3 *(0°С-(-10° ))=189 Дж
кг°с м3
Q2= λ* m; Q2=340000
Q3=4200
Дж
кг°С
Дж
кг
*0,09кг=30600Дж
*0,09кг*50° С + 18900Дж
Q=189Дж+30600Дж+18900Дж=49689Дж
49689 Дж
t=
200Вт
= 24.8445 с
t=24.8445C
Время плавления на одного «гриба» с утюгом 24, 8445 с, с учетом
дополнительных потерь 24,8445+20 = 44,8445 с.
Всего «грибов» - 500. Значит, 500 * 44,8445= 22500с = 6,25 часов.
Ответ: на «выглаживание» катка уйдет 6.25 часов и Петя в воскресенье
сможет покататься.
7. Решение: Обозначим длину Кита L, тогда его радиус R =
𝐿
/
20
По представлениям того времени, Кит и Земля находятся в однородном
гравитационном поле.
Если суммарная масса Кита и Земли не больше массы воды в объеме Кита, то
можно записать
2
3
𝜋𝜌з*𝑅3 + 20 r 𝜋 𝑟 2 𝜌к ≤ 20 r 𝜋 𝑟 2 𝜌в
2
20 r 𝜋 𝑟 2 𝜌в - 20 r 𝜋 𝑟 2 𝜌к ≥ 𝜋𝜌з*𝑅3
3
2
𝑟 3 (20 𝜋 𝜌в - 20 𝜋 𝜌к) ≥ 𝜋𝜌з*𝑅3
3
3
𝜌з
r≥ √
*Rз
30(𝜌в−𝜌к)
ρз=5,5 г/см
3
3
=5500кг/м3 ; ρК=0,9 г/см
= 900кг/ 3
м ;
3
5500кг/м3
r≥ √
900кг/м3 ) * 6400000м =8700000м=8700км. Тогда длина
30(5500кг/м3 −
Кита должна быть не меньше 174000км. Значит эта оценка несколько
занижена, так как для устойчивого плавания необходимо, чтобы Кит
погружался в воду.
8. Решение:
Чтобы успеть на автобус, зайка должен выйти в 7,47, а чтобы успеть на
трамвай – в 7,45.
У Знайки есть два варианта поведения: идти к остановке А или к остановке
В, соответственно, он должен выбрать тот из них, который требует меньше
времени, чтобы попасть на остановку В.
Пусть Знайка хочет успеть на автобус. Если он пойдет на остановку В, то он
должен выйти за (2 км-0,8 км)/4,8 км/ч =15 мин. до 8 часов. Если же он
пойдет на остановку А, то чтобы успеть на автобус, ему необходимо прийти
туда не к 8.00, а на 2 км/40 км /ч = 3 ч мин. Раньше, поэтому ему надо выйти
за 0,8км/4,8км/ч+3мин=13мин. До 8,00.Поэтому в этом случае для Знайки
выгоднее идти к остановке идти к остановке А и нужно выйти из дома в 7.47.
Аналогичные рассуждение для случая, когда Знайка идет к Остановке В, то
он должен выйти за 15 минут до 8.00, а если к А то за 16 минут до 8.00,
поэтому Знайка должен выйти в 7.45 и пойти к остановке В.
Ответ: Чтобы успеть на автобус, Знайка должен выйти в 7.47; а чтобы успеть
на трамвай – в 7.45.
9. Решение:
Время погони (t = Sулитки /Vулитки) ; t = 100 : 0,002 = 50 000 с.
Кролик за это время пробежал (Sкролика= Vкролика t) ; Sкролика= 0,628 * 50
000 = 31 400 м.
Один круг кролик пробегает примерно за (Т = 2πR/V);Т = (2*3,14 *
100) /0,628 = 1000 с.
Число кругов (N= t/ Т); N = 50 000/1000 = 50.
Расстояние «по дуге» примерно 0 м. (31400 м - 31400 м = 0 м ).
Следовательно движение закончится в начальной точке, т.е кролик находиться
в первоначальной точке.
Ответ: движение закончится в начальной точке, т.е кролик находиться в
первоначальной точке.
10. Решение
m1 = m2 = m3 = 2*m4 – m0 = 2 кг – 0,3 кг = 1,7 кг