х 1 - Северо-Кавказский горно
реклама

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
В ЭКОНОМИКЕ
Методические указания к лабораторным работам
для студентов, обучающихся по направлениям подготовки
080100.62 "Экономика", 080200.62 "Менеджмент"
Составители:
М. Д. Джиникаев, Н. А. Цгоева, Д. А. Дегтярева
Владикавказ 2015
0
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"СЕВЕРО-КАВКАЗСКИЙ ГОРНО-МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ)"
Кафедра "Информационные системы в экономике"
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
В ЭКОНОМИКЕ
Методические указания к лабораторным работам
для студентов, обучающихся по направлениям подготовки
080100.62 "Экономика", 080200.62 "Менеджмент"
Составители:
М. Д. Джиникаев, Н. А. Цгоева, Д. А. Дегтярева
Владикавказ 2015
1
УДК 004.7:65.01:33
ББК 73:65
Д41
Рецензент
доктор технических наук,
профессор Северо-Кавказского горно-металлургического института
(государственного технологического университета)
Кумаритов А. М.
Д41
Компьютерное моделирование в экономике: Методические указания к лабораторным работам для студентов, обучающихся по направлениям подготовки 080100.62 "Экономика", 080200 "Менеджмент" /
Сост. М. Д. Джиникаев, Н. А. Цгоева, Д. А. Дегтярева; СевероКавказский горно-металлургический институт (государственный технологический университет). – Владикавказ: Северо-Кавказский горнометаллургический институт (государственный технологический университет). Изд-во «Терек», 2015. – 40 с.
Методические указания предназначены для формирования комплекса
знаний, умений и навыков, необходимых для анализа современных проблем в
области производства, финансов и кредитов; поиска оптимальных решений
стратегических и тактических задач организационного управления. Рекомендовано для студентов направлений подготовки 080100.62 "Экономика",
080200.62 "Менеджмент".
УДК 004.7:65.01:33
ББК 73:65
Редактор: Хадарцева Ф. С.
Компьютерная верстка: Цишук Т. С.
Составление. ФГБОУ ВПО «Северо-Кавказский
горно-металлургический институт
(государственный технологический университет)», 2015
Джиникаев М. Д., Цгоева Н. А.,
Дегтярева Д. А., составление, 2015
Подписано в печать 06.11.2015. Формат 60 х 84 1/16. Бумага офсетная. Гарнитура «Таймс».
Печать на ризографе. Усл. п.л. 2,33. Уч.-изд. л. 2,5. Тираж 30 экз. Заказ № .
Северо-Кавказский горно-металлургический институт (государственный технологический
университет). Издательство «Терек».
Отпечатано в отделе оперативной полиграфии СКГМИ (ГТУ).
362021, г. Владикавказ, ул. Николаева, 44.
2
ОРГАНИЗАЦИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
Лабораторные работы по курсу «Компьютерное моделирование в экономике» охватывают большинство тем курса и содержат четыре лабораторные
работы: решение финансовых задач с помощью MS Excel (лабораторная работа
№ 1); решение и анализ финансово-экономических задач средствами MS Excel
(лабораторная работа № 2); задачи линейного программирования (лабораторная
работа № 3) и задачи оптимальных перевозок (лабораторная работа № 4).
Особенностью лабораторных работ является их компьютерная направленность. В качестве программной среды используются средства MS Excel.
Техническое обеспечение – это персональные компьютеры любой современной
конфигурации.
Организация выполнения каждой лабораторной работы протекает в несколько этапов и предусматривает:
1. Составление отчета.
Отчет должен быть оформлен на отдельных листах формата А4, либо в
тетради с обязательным указанием номера группы, ФИО исполнителя, номера и
названия лабораторной работы. Отчет должен содержать цель работы, основные сведения по теории. После выполнения работы студенты записывают условие задачи и ход её решения, приводят таблицы и графики экспериментальных
зависимостей показателей, делают выводы о причинно-следственных связях и
взаимном влиянии факторов, сравнивают полученные результаты с теоретическими положениями учебников.
2. Выполнение работы.
Сначала студент на основе усвоения основных теоретических положений
и общей постановки задачи, получает самостоятельно на компьютере правильный ответ тестового примера. Студент показывает его преподавателю, который
проверяет полученные результаты и после этого выдает студенту одно из индивидуальных заданий, приведенных в конце лабораторной работы. Студент приступает к выполнению полученного индивидуального задания. Полученные результаты на компьютере студент предъявляет преподавателю для проверки.
3. Сохранение результатов выполненной работы.
Результаты выполнения работы студент сохраняет на жестком диске в
папке «Мои документы\КМЭ» под именем ФИО_Работа№_Вариант№ (например, ИвановАП_Работа№1_Вариант№3) и на съемном носителе информации.
Записать результаты в отчет.
4. Представление результатов выполнения работы (отчета и файлов) для
проверки преподавателю.
5. Защита выполненной работы.
Ответы на контрольные вопросы по теоретическому материалу и на замечания преподавателя по выполненной работе.
3
Лабораторная работа № 1
Решение финансовых задач с помощью MS Excel
Цель работы: – изучение некоторых финансовых функций;
– приобретение навыков использования функций Excel для
решения задач финансового анализа;
– решение типичных финансовых задач с помощью Excel.
1.1. Функции MS Excel
С помощью формул и функции в Excel можно выполнять математическую и статическую обработку данных, а также решать типичные финансовые
задачи. Неоспоримым преимуществом электронной таблицы Excel является то,
что при изменении данных листа результаты вычислений моментально обновляются. Excel делит все функции на следующие категории [1, 2]:
1.
Финансовые (Financial) – функции для расчета амортизации имущества, стоимости основных фондов, нормы прибыли, величины выплат на основной капитал и других финансовых показателей.
2.
Дата и время (Date & Time) – операции прямого и обратного преобразования даты и времени в текстовые строки.
3.
Математические (Math & Trig) – математические и тригонометрические функции.
4.
Статистические (Statistical) – функции для расчета среднего значения, дисперсии, статистических распределений и других вероятностных характеристик.
5.
Ссылки и массивы (Lookup & Reference) – операции преобразования
ссылки на ячейку в число, расчета ссылок на основе числовых аргументов, вычисление числа строк и столбцов диапазона и других параметров, связанных с
адресацией ячеек листа Excel.
6.
Работа с базой данных (Database) – функции формирования выборки из базы данных и расчета статистических параметров величин, расположенных в базе данных.
7.
Текстовые (Text) – функции для работы с текстовыми строками.
8.
Логические (Logical) – функции для работы с данными логического
типа, то есть величинами или условиями, принимающими значение Истина
или Ложь.
9.
Проверка свойств и значений (Information) – функции проверки типа данных аргумента, режима форматирования ячейки, типа сгенерированной
ошибки и других специальных условий.
В списке Категория (Function Category) есть также пункты Полный алфавитный перечень (All) и 10 недавно использовавшихся (Most Recently Used), которые выводят соответственно список всех функции и 10 функций, применявшихся последними.
4
1.2. Некоторые часто используемые финансовые функции
1.
ПС – возвращает приведенную (к текущему моменту) стоимость
инвестиции. Приведенная (нынешняя) стоимость представляет собой общую
сумму, которая на настоящий момент равноценна ряду будущих выплат.
Например, когда вы занимаете деньги, сумма займа является приведенной (нынешней) стоимостью для заимодавца.
Синтаксис: ПС (ставка; кпер; плт; бс; тип)
2.
БС – возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки.
Синтаксис: БС (ставка; кпер; плт; пс; тип)
3.
КПЕР – возвращает общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной
ставки.
Синтаксис: КПЕР (ставка; плт; пс; бс; тип)
4.
ПЛТ – возвращает сумму периодического платежа для аннуитета
на основе постоянства сумм платежей и постоянства процентной ставки.
Синтаксис: ПЛТ (ставка; кпер; пс; бс; тип)
Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и
платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.
5.
СТАВКА – возвращает процентную ставку по аннуитету за один
период. СТАВКА вычисляется путем итерации и может давать нулевое значение
или несколько значений. Если последовательные результаты функции СТАВКА
не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО!.
Синтаксис: СТАВКА (кпер; плт; пс; бс; тип; предположение).
1.3. Аргументы финансовых функций
Аргументы, набранные жирным шрифтом, являются обязательными,
остальные аргументы могут отсутствовать.
Ставка – процентная ставка за период. Например, если получена ссуда на
автомобиль под 10 процентов годовых и делаются ежемесячные выплаты, то
процентная ставка за месяц составит 10%/12 или 0,83%. В качестве значения
аргумента ставка нужно ввести в формулу 10%/12 или 0,83% или 0,0083.
кпер – общее число периодов платежей по аннуитету. Например, если получена ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то
ссуда имеет 4 12 (или 48) периодов. В качестве значения аргумента кпер в
формулу нужно ввести число 48.
плт – выплата, производимая в каждый период и не меняющаяся за все
время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включают других сборов или налогов. Например, ежемесячная выплата по четырехгодичному займу в 10 000 р. под 12 процентов го5
довых составит 263,33 р. В качестве значения аргумента выплата нужно ввести
в формулу число 263,33.
бс – требуемое значение будущей стоимости или остатка средств после
последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая
стоимость займа, например, равна 0). Например, если предполагается накопить
50 000 р. для оплаты специального проекта в течение 18 лет, то 50 000 р. – это и
есть будущая стоимость. Можно сделать предположение о сохранении заданной процентной ставки и определить, сколько нужно откладывать каждый месяц.
пс – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
тип – число 0 или 1, обозначающее, когда должна производиться выплата
(0 или опущен – в конце периода, 1 – в начале периода).
прогноз (предположение) – предполагаемая величина ставки. Если значение предположения опущено, то оно полагается равным 10 процентам. Если
функция СТАВКА не сходится, попробуйте подставить различные значения для
предположения. СТАВКА обычно сходится, если величина предположения
находится между числами 0 и 1.
Все аргументы, означающие денежные средства, которые должны быть
выплачены (например сберегательные вклады), представляются отрицательными числами, денежные средства, которые должны быть получены (например
дивиденды), представляются положительными числами.
Аннуитет – это ряд постоянных денежных выплат, делаемых в течение
длительного периода. Например, заем под автомобиль или заклад являются аннуитетами.
1.4. Примеры решения задач с использованием финансовых функций Exсel
1.
Рассчитать, какая сумма окажется на счете, если 270 тыс. р. положены на 3 года под 18,5 % годовых. Проценты начисляются один раз в год.
Запускаем приложение Excel, в строке формул нажимаем кнопку fx или
выбираем команду Вставка → Функция, откроется диалоговое окно Мастер
функции.
6
В раскрывающем списке категория выбираем Финансовые, а в списке
функции – функцию БС и в открывшемся диалоговом окне вводим аргументы
функции, как показано на рис. 1.1.
Ответ: БС (ставка; кпер; плт; пс; тип) = БС(18,5 %; 3; ; –270 000) =
= 449 281 р. 79 к.
2.
Условия те же, но начисление процентов производится раз в полгода (см. рис. 1.2).
Ответ: БС (ставка; кпер; плт; пс; тип) = БС(18,5 % / 2;3*2; ; –270 000) =
= 459 084 р. 30 к.
3.
На счет в банке вносится сумма по 10 тыс. руб. в течении 10 лет в
начале каждого года. Годовая ставка 4 %. Какая сумма будет на счете через 10
лет? (см. рис. 1.3).
Ответ: БС (ставка; кпер; плт; пс; тип) = БС(4 %; 10; –10 000; ;1) =
= 124 863 р. 51 к.
7
Рис. 1.1. Ввод аргументов функции БС
Рис. 1.2. Ввод аргументов функции БС
8
Рис. 1.3. Ввод аргументов функции БС
4.
К примеру, мы хотим накопить 200 тыс. р. за 5 лет, положив некоторую сумму в банк при условии начисления 15 % годовых ежегодно. Найти
эту первоначальную сумму (см. рис. 1.4).
Рис. 1.4. Ввод аргументов функции ПС
Ответ: ПС (ставка; кпер;плт; бс; тип)=ПС(15 %; 5 ; ; 200000) = –99 435 р. 35 к.
Проведем проверку: БС(15%;5;; –99 435,35)=200000 р., таким образом
значение совпало с аргументом Бс функции ПС.
5. Фирме потребуется 500 тыс. р. через 12 лет. Определить необходимую
сумму вклада, если ставка процента по нему составляет 12 % в год (рис. 1.5).
9
Рис. 1.5. Ввод аргументов функции ПС
Ответ: ПС (ставка; кпер; пс; бс; тип)=ПС(12%;12;500 000) = –128337 р. 55 к.
6. Рассчитать размер периодического ежемесячного платежа кредита
размером 300 000 р., выданного на 3 года, с процентной ставкой 6 % годовых.
Ответ: ПЛТ (ставка; кпер; пс; бс; тип) = ПЛТ(6 % /12; 3*12; 300 000) = –9 126 р 58 к.
7. Рассмотрим обратную задачу. Рассчитать количество периодов выплаты 6 %-го кредита, размером 300 тыс. р. с ежемесячной выплатой –9 126,58 р.
Для решения используем функцию КПЕР (рис 1.6).
Рис. 1.6. Ввод аргументов функции КПЕР
10
КПЕР (ставка; плт; пс; бс; тип)=КПЕР(6 % /12; –9 126,58; 300 000) = 36.
Ответ: Количество периодов выплат составит 36 месяцев или 3 года.
Отсюда следует, что функция КПЕР обратна функции ПЛТ.
8.
Определить процентную ставку для 7-летнего займа в 250 000 р. с
ежемесячной выплатой в 5500 р. Решение задачи показано на рис. 1.7.
Рис. 1.7. Ввод аргументов функции СТАВКА
СТАВКА (кпер; плт; пс; бс; тип; предположение) = СТАВКА (7*12; –5 500; 250 000)=
= 2 %, т. к. это месячная процентная ставка, то годовая процентная ставка составит 2 %*12 = 24 %.
Ответ: Годовая процентная ставка составит 24 %.
9.
Выполнить расчет 20-летней ипотечной ссуды покупки квартиры за
3 500 000 р. с годовой ставкой 13 % и начальным взносом 30 %. Сделать расчет
ежегодных и ежемесячных выплат.
Для решения данной задачи необходимо использовать функцию ПЛТ. Решение данной задачи показано на рис. 1.8 и 1.9. На рис. 1.8 указаны необходимые
формулы для решения задачи, а на рис.1.9 – полученные результаты.
11
Рис. 1.8. Формулы для решения задачи
Рис. 1.9. Результаты расчета
1.5. 3адачи для самостоятельного решения
1. Вычислить значение суммы на расчетном счете по истечении 5 лет,
если в банке размещено 200 000 р. под 8 % годовых и начисление процентов
производится один раз в полгода. Проверить результат.
2. Ссуда в 150 000 р. дана на полтора года под ставку 22 % годовых с
ежеквартальным начислением. Определить сумму конечного платежа.
3. Рассмотреть два варианта покупки дома: заплатить сразу 2 300 000 р.
или в рассрочку – по 20 500 р. ежемесячно в течение 15 лет. Определить, какой
12
вариант предпочтительнее, если ставка процента – 8 % годовых.
4. Ссуда размером 66 000 р., выданная под 36 % годовых, погашается
ежемесячными платежами 6630 р. Рассчитать срок погашения ссуды.
5. Рассчитать процентную ставку для четырехлетнего займа в 170 000 р.
с ежемесячными погашением по 4500 р.
6. Рассчитать платежи по процентам трехгодичного займа в 800 000 р. из
расчета 10 % годовых.
1.6. Задания
2. Вычислить N-годичную ипотечную ссуду покупки квартиры за Р р. с
годовой ставкой I % и начальным взносом А %. Сделать расчет ежемесячных и
ежегодных выплат.
№ вар.
1
2
3
4
5
6
7
8
9
10
N, лет
7
5
4
6
5
4
3
4
5
6
P, руб. 800 000 950 000 870 000 690 000 950 000 880 000 670 000 890 000 1 000 000 895 000
I, %
11
12
14
13
15
12
15
16
10
13
A, %
25
40
30
15
35
20
10
16
22
33
3. Вы берете в долг Р р. под годовую ставку I % и собираетесь выплачивать по A р. в год. Сколько лет займут эти выплаты?
№ вар.
P, руб.
I, %
A, руб.
1
8 000
11
2 500
2
9 000
12
1 400
3
8 700
14
2 300
4
6 000
13
1 450
5
9 500
15
2 305
6
8 800
12
2 500
7
6 700
15
1 900
8
8 900
16
2 160
9
10 000
10
1 220
10
8 900
13
2 033
4. Вас просят дать в долг Р р. и обещают возвращать по А р. в течение N
лет. При какой годовой процентной ставке эта сделка имеет?
№ вар.
P, руб.
N, лет
A, руб.
1
8 000
4
2 500
2
9 000
12
1 400
3
8 700
5
2 300
4
6 000
8
1 450
5
9 500
10
1 305
6
8 800
12
1 520
7
6 700
15
900
8
8 900
16
860
9
10 000
10
1 220
10
8 900
13
903
5. Вы собираетесь вкладывать по А руб. в течение N лет при годовой
ставке I %. Сколько денег будет на счете через N лет?
№ вар.
N, лет
I, %
A, руб.
1
8
11
250
2
9
12
400
3
7
14
230
4
6
13
140
5
9
15
130
6
8
12
520
7
7
15
1 900
8
8
16
810
9
1
10
720
10
9
13
903
6. Определить процентную ставку для N – летнего займа в Р р. с ежемесячной выплатой А р.
№ вар.
P, руб.
N лет
A, руб.
1
8 000
11
200
2
9 000
12
400
3
8 700
14
300
4
6 000
13
150
5
9 500
15
105
13
6
8 800
12
200
7
6 700
15
100
8
8 900
16
160
9
10 000
10
220
10
8 900
13
303
1.7. Контрольные вопросы
1. Перечислите известные вам категории функции Excel. В чем их
назначение?
2. Перечислите известные вам финансовые функции.
3. Перечислите аргументы финансовых функций.
4. Назначение функций ПЛТ, БС, ПС, ЧПС, КПЕР, СТАВКА?
5. Назначение аргументов финансовых функций.
6. Что такое процент? В каких случаях удобно использовать при расчётах проценты?
7. В чем отличие между простыми и сложными процентами?
8. Что такое дисконтирование?
14
Лабораторная работа № 2
Решение и анализ финансово-экономических задач средствами MS Excel
Цель работы:
– приобретение навыков использования средств Excel для
финансово-экономического анализа и прогнозирования;
– решение финансово-экономических задач с помощью
Подбора параметра и Сценариев.
2.1. Подбор параметра
Когда желаемый результат одиночной формулы известен, но неизвестны
значения, которые требуется ввести для получения этого результата, можно
воспользоваться средством Подбор параметра. Пои этом Excel изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой
ячейки, не возвращает нужный результат [2, 3].
Подбор параметра вызывается командой Данные Анализ «что - если…» Подбор параметра…
Рассмотрим использование инструмента Подбор параметра на следующих задачах [4].
Задача 1. Вас просят дать в долг 100 000 р. и обещают вернуть 20 000 р. –
через год, 40 000 р. – через 2 года и 70 000 р. – через 3 года. При какой годовой
процентной ставке эта сделка имеет смысл?
Для решения данной задачи необходимо использовать финансовую функцию ЧПС.
ЧПС – возвращает величину чистой приведенной стоимости инвестиции,
используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения) [2, 4].
Синтаксис: ЧПС(ставка ; значение1; значение2; ...)
ставка – ставка дисконтирования за один период.
значение 1, значение 2, ... – от 1 до 29 аргументов, представляющих расходы и доходы.
Значение 1, значение 2, ... должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
ЧПС использует порядок аргументов значение 1, значение 2, ... для определения порядка поступлений и платежей. Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел, учитываются. Аргументы, которые являются значениями ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются.
Если аргумент является массивом или ссылкой, то учитываются только
числа. Пустые ячейки, логические значения, текст или значения ошибок в массиве или ссылке игнорируются.
Считается, что инвестиция, значение которой вычисляет функция ЧПС,
начинается за один период до даты денежного взноса значение 1 и заканчивает15
ся с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов.
ЧПС аналогична функции ПС (текущее значение). Основное различие
между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от
денежных взносов переменной величины в функции ЧПС, денежные взносы в
функции ПС должны быть постоянны на весь период инвестиции.
Решение:
На рабочий лист вводим исходные данные, как показано на рис. 2.1.
В ячейку С6 введем функцию = ЧПС(C5; C2: C4).
Первоначально в ячейку С5 вводим произвольный процент, например
5 %, Затем командой Данные Анализ «что - если…» Подбор параметра…, откроется диалоговое окно Подбор параметра и вводим данные.
В поле Установить в ячейке: вводим $C$6;
в поле Значение: – 100 000;
в поле Изменяя значение ячейки вводим адрес ячейки $C$5.
После нажатия кнопки OK, появится диалоговое окно Результат подбора
параметра (рис. 2.2) с результатами расчета.
• приведенная стоимость займа – 100 000 р.;
• процентная ставка – 11,79 % (приблизительно 12 %).
Рис. 2.1. Исходные данные
16
Рис. 2.2. Результаты расчета
2.2. Сценарий
Сценарием в Microsoft Excel называется набор значений подстановки, используемый для прогнозирования поведения какой-либо модели. Существует
возможность создания и сохранения на листе различных сценариев и переключения на любой из этих сценариев для просмотра результатов. Taк, если требуется сформировать бюджет, но годовой доход точно не известен, то для дохода
определяются различные значения, а затем для каждого сценария выполняется
анализ «что – если» [2].
Задача 3. Вас просят дать в долг 100 000 р. и обещают возвращать по
20 т. р. в течение 6 лет. Будет ли выгодна эта сделка при годовой процентной
ставке 7 %.
Решение:
Введем исходные данные в соответствии с рис. 2.3. В ячейку В5 запишем
формулу = ПС(B4; B2; –B3).
17
Рис. 2.3. Исходные данные
Для наглядности полученного решения в ячейку В6 введем следующее
выражение:
= ЕСЛИ (B1 < B5; "Выгодно дать в долг";
ЕСЛИ (B1 = B5;
"Варианты равнозначны";
ЕСЛИ (B1 > B5; "Выгодно положить под проценты"))).
Часто бывает удобно проанализировать ситуацию для нескольких возможных вариантов параметров. Для этого служит команда Данные Анализ
«что - если…» Диспетчер сценариев…
Рассмотрим применение этой команды для 3-х комбинаций срока и суммы ежегодно возвращаемых денег:
• 6 лет и 22 000 р.;
• 10 лет и 15 000 р.;
• 8 лет и 16 000 р.
Выполним команду Данные Анализ «что - если…» Диспетчер сценариев… На экране появится диалоговое окно Диспетчера сценариев, в котором
нужно нажать кнопку Добавить. После этого откроется следующее диалоговое
окно Добавление сценария, в котором нужно ввести имя сценария, например
Сц1, и адреса изменяемых ячеек, в данном случае это В3:В4 (рис 2.4).
После нажатия кнопки OK на следующем шаге появится диалоговое окно
Значения ячеек сценария, показанное на рис. 2.5. В соответствующих полях
ввода необходимо ввести значения изменяемых ячеек и нажать кнопку Добавить. После этого последовательно появятся диалоговые окна Добавление сце18
нария (рис. 2.4) и Значения ячеек сценария (рис. 2.5), в которых надо указать
соответствующие данные для второго сценария Сц2: срок 10 лет и ежегодная
сумма 15 000 р. Нажав кнопку Добавить необходимо все шаги аналогично провести для третьего сценария Сц3 с исходными данными 8 лет и 16 000 р. и
нажать кнопку OK (рис. 2.6).
Рис. 2.4. Диалоговое окно Добавление сценария
Рис. 2.5. Диалоговое окно Значение ячеек сценария
После этого в окне Диспетчера сценариев, нажать кнопку Отчет. На
экране появится диалоговое окно Отчет по сценарию, в котором надо указать
тип отчета, например Структура и ввести адреса ячеек результата, в данном
случае В5:В6. Нажав кнопку ОК, появится лист Структура сценария с отчетом
и результатами решения данной задачи, показанный на рис. 2.7.
Как видно из листа, в третьем случае выгодно положить деньги под проценты, а в первом и во втором случаях – дать в долг. Если после внесения из19
менений в сценарий он будет сохранен с первоначальным именем, то новые
значения изменяемых ячеек заменят значения в исходном сценарии.
Рис. 2.6. Диалоговое окно Диспетчер сценариев
Рис. 2.7. Результат решения задачи
2.3. Задания
1.
Вас просят дать в долг Р р. и обещают вернуть Р1 р., через год, Р2 р.
через 2 года и Рп р. через N лет. При какой годовой процентной ставке эта сделка имеет смысл?
20
№ вар.
N, лет
Р, руб.
Р1, руб.
Р2, руб.
Р3, руб.
Р4, руб.
1
4
17 000
5 500
8 000
2 500
3 000
2
3
20 000
8 500
6 000
7 000
3
4
5
3
2
4
18 500 5 000 12 000
6 500 2 000 1 500
6 500 3 500 2 500
7 500
4 000
6 000
6
4
2 500
500
800
1 000
400
7
8
3
2
3 600 5 600
850 3400
950 2400
2000
9
4
4 500
1 300
1 100
1 500
1 200
10
4
52 500
19 000
20 500
5 500
10 000
2. Вас просят дать в долг А р. и обещает возвращать по Р р. в течение N лет.
Будет ли выгодна эта сделка при годовой процентной ставке I %.
Проанализируйте ситуацию для 3-х возможных комбинаций срока, суммы ежегодно возвращаемых денег и годовой процентной ставки:
• N1 лет, P1 р. и I1 %;
• N2 лет, P2 р. и I3 %;
• N3 лет, P3 р. и I4 %.
№ вар.
А, руб.
Р, руб.
N, лет
I, %
Р1, руб.
N1, лет
I1 , %
Р2, руб.
N2, лет
I2 , %
Р3, руб.
N3, лет
I3 , %
1
2
3
5 500 4 900 8 900
1 300 1 400 2 300
5
4
4
6
6
1
1 250 1300 2 400
7
5
5
7
6
3
1 350 1250 2 350
5
7
5
6
5
2
1 400 1500 2 500
6
4
4
7
7
3
4
9 500
3 300
3
2
3 500
3
4
3 400
5
6
4 000
3
8
5
7 600
1 700
6
9
1 600
9
6
1 800
5
6
1 700
9
6
6
6 800
1 900
4
5
1 900
5
4
2 000
4
8
1 700
7
3
7
5 300
1 400
4
2
1 300
5
3
1 400
5
5
1 500
4
6
8
7 400
1 800
5
7
1 750
7
5
1 900
4
3
2 000
5
9
9
8 500
1 500
6
2
4 500
2
6
2 500
4
5
1 600
10
3
2.4. Контрольные вопросы
1.
2.
3.
4.
5.
6.
Поясните алгоритм средства Подбор параметра?
В чем назначение средства Сценарии?
Какие числовые форматы вы знаете?
Чем отличаются денежный и финансовый форматы?
Что такое маркер копирования?
Перечислите назначение кнопок панели инструментов Excel.
21
10
9 700
2 400
5
8
2 200
8
5
2 500
5
6
2 300
9
9
Лабораторная работа № 3
Задачи линейного программирования
Цель работы:
– освоить решение оптимизационных задач линейного
программирования с помощью MS Excel;
– получить навыки использования задач распределения
ресурсов в хозяйственной деятельности современных
предприятий и организаций.
3.1. Основные сведения
Задачи линейного программирования (ЗЛП) представляют собой оптимизационные задачи, описываемые линейными математическими моделями. Различные аспекты оптимизации занимают очень важное место в бизнесе и деятельности современных организаций и предприятий [3, 5]. Проблемы оптимизации присутствуют в самых различных процессах, которые можно грубо разделить на следующие категории:
- оптимизация перевозок грузов;
- оптимизация распределения ресурсов (в самом широком смысле – от
распределения производственных мощностей для выпуска нескольких
(многих) видов товаров с различной прибыльностью до оптимизации состава стада крупного рогатого скота для наиболее прибыльного производства молока и мяса);
- оптимизация расхода/раскроя материалов и т.д.
В общем виде постановка оптимизационной задачи математического программирования состоит в определении таких значений переменных х1, х2, …, хп,
при которых целевая функция достигает наибольшего или наименьшего значения
f(x1, x2, …, xn) → max (или min),
а сами переменные удовлетворяют одновременно системе ограничений
gi(x1, x2, …, xn) ≤ (≥) bi, i=1, 2, …, m,
где f и gi – заданные функции, bi – заданные числа.
Если все функции f и gi линейны, то соответствующая задача математического программирования является ЗЛП. Линейность предполагает наличие двух
свойств: пропорциональности и аддитивности. Пропорциональность означает,
что вклад каждой переменной в целевую функцию и ограничения прямо пропорционален величине этой переменной. Аддитивность заключается в том, что
и целевая функция, и ограничения для каждого значения индекса i представляют собой сумму вкладов от различных переменных.
Математическая модель ЗЛП в общем случае формулируется следующим
образом [5, 6].
Найти значения неотрицательных переменных x1, x2, …, xn, доставляющих
максимум (или минимум) линейной целевой функции
F = c1x1 + c2x2 + … +cnxn → max (или min),
22
удовлетворяющих одновременно всем ограничениям – неравенства/равенствам:
a11 x1 a12 x 2 a1n x n (, )b1 ,
a x a x a x (, )b ,
21 1
22 2
2n n
2
a m1 x1 a m 2 x 2 a mn x n (, )bm .
Содержательный смысл рассматриваемых в линейном программировании задач требует также выполнения условий неотрицательности переменных
x1 ≥ 0, x2 ≥ 0, …, xn ≥ 0.
Рассмотрим решение ЗЛП на примере задачи распределения ресурсов.
Организация производит три вида продукции (П1, П2, П3), на их производство затрачиваются три ресурса (Р1, Р2, Р3, например, время работы оборудования, денежные средства и сырьё). На изготовление одной единицы продукции П1 затрачивается 1 усл.ед. Р1, 7 усл.ед. Р2 и 4 усл.ед. Р3. На изготовление
П2 затрачиваются соответственно: 1 усл.ед. Р1, 2 усл.ед. Р2, 8 усл.ед. Р3, а на
П3 соответственно затрачиваются: 1 усл.ед. Р1, 4 усл.ед. Р2 и 10 усл.ед. Р3.
Организация имеет на своем складе запас ресурсов в количестве 20 усл.ед.
Р1, 100 усл.ед. Р2 и 200 усл.ед. Р3. Руководству организации необходимо определить план выпуска продукции, при котором прибыль от её реализации будет
максимальной. Если реализация одной единицы продукции вида П1 приносит
80 ден.ед. прибыли, продукции вида П2 – 100 ден.ед. прибыли, а П3 – 50 ден.ед.
прибыли.
Математическая модель
Переменные. Так как необходимо определить объёмы производства каждого вида продукции, переменными в модели являются: x1 – количество произведенной продукции вида П1, x2 – количество произведенной продукции вида
П2 и x3 – количество произведенной продукции вида П3.
Целевая функция. Руководство организации желает получить максимальную прибыль от реализации произведенных организацией продукции.
Поэтому целевая функция должна представлять собой суммарную прибыль от
реализации произведенной продукции. Так как прибыль от реализации одного
вида продукции П1 равна 80 ден. ед., то прибыль от его реализации составить
80x1 ден. ед. Аналогично, прибыль от реализации x2 продукции вида П2 составить 100x2 ден.ед., и для продукции вида П3 – 50x3 ден. ед.
Целевая функция, выражающая суммарную прибыль от реализации выпускаемой фирмой продукции, будет равна:
F 80 x1 100 x2 50 x3 max .
Ограничения. Ограничения в математической модели отражают ограниченность ресурсов, используемых при производстве продукции.
Запишем ограничение на расход ресурса Р1. Поскольку на производство
одной единицы продукции вида П1 затрачивается 1 усл. ед. Р1, то на производство продукции П1 в объеме х1 будет затрачено в объеме 1х1. Аналогично на
производство продукции П2 в объеме х2 будет затрачено 1х2 Р1, для производства П3 в объеме х3 – 1х3 Р1.Тогда суммарный расход Р1 составит х1 + х2 + х3 и
23
он не может превосходить имеющегося на складе объема (20 усл. ед.). Таким
образом получаем первое ограничение на расход ресурса Р1:
х1 х2 х3 20.
Ограничение на использование ресурса Р2 можно записать следующим
образом. На изготовление одной единицы продукции П1 затрачивается 7 усл.ед.
ресурса Р2, а на изготовление в объеме х1 – 7х1, аналогично для П2 в объеме х2 –
2х2, для П3 в объеме х3 – 4х3 ресурса Р2. Суммарный расход ресурса Р2 для
производства трех видов продукции составит 7х1 + 2х2 + 4х3 и не может превышать запасов ресурса Р2 (100 усл.ед.). Тогда ограничение на ресурс Р2 можно
записать в виде:
7 х1 2 х2 4 х3 100.
Точно так же составляется ограничение на ресурс Р3, которые ограничены 200 усл. ед. На изготовление одной единицы продукции П1 требуется 4 усл.
ед. Р3, а в объеме х1 – 4х1 Р3.Анологично для П2 расход ресурса Р3 в объеме х2
составит 8х2, а для П3 – 10х3. Суммарные затраты ресурса Р3 составит
4х1 + 8х2 + 10х3,
получаем третье ограничение:
4 х1 8х2 10 х3 200.
По смыслу задачи объемы выпускаемой продукции не могут быть отрицательными, поэтому к приведенным выше ограничениям необходимо добавить еще три:
х1 0, х2 0, х3 0.
Таким образом, получаем следующую математическую модель задачи:
F 80 x1 100 x2 50 x3 max,
x1 x2 x3 20,
7 x1 2 x2 4 x3 100 ,
(3.1)
4 x1 8 x2 10 x3 200 ,
x1 0, x2 0, x3 0.
Математическая модель линейна поскольку переменные х1, х2 и х3 входят
в нее в первой степени.
Решение задачи средствами Excel.
В Excel имеется стандартный механизм разрешения подобных задач заключенный в надстройке Поиск решения. Для его использования необходимо
активировать данную надстройку: Кнопка «Office» → Параметры Excel →
Надстройки. Далее в открывшемся диалоговом окне Надстройки активируем
элемент списка Поиск решения следующим образом: Управление → Надстройки Excel → Перейти → Поиск решения. После этого данный элемент станет доступен в меню Данные.
24
Рис. 3.1. Кнопка «Office»
Рис.3.2. Поиск решения
25
Теперь необходимо ввести исходные данные на лист Excel для решения
задачи. Форма должна выглядеть, как показано на рис. 3.3.
Коэффициенты целевой функции, представленные в ячейках диапазона
B4:D4, a объемы производства, которые будут после решения задачи представлены в ячейках B3:D3, то формула расчета целевой функции должна рассчитывать сумму произведений ячеек B3:D3 на B4:D4.
Для расчета суммы произведений диапазонов ячеек в Excel предусмотрена математическая функция СУММПРОИЗВ.
Для расчета целевой функции необходимо в ячейку F4 ввести формулу:
=СУММПРОИЗВ(B3:D3;B4:D4).
Теперь необходимо ввести ограничения на использование ресурсов – систему неравенств-ограничений, согласно математической модели (3.1).
Каждое неравенство выражает ограничение объемов производства различных видов продукции имеющимся количеством данного ресурса. Столбец
Расход ресурсов представляет собой сумму произведений количества ресурса,
требуемого на производство единицы продукции на объем производства данного вида продукции. Столбец Запасы ресурсов отражает количество ресурса, которое имеется на складе.
Так как объемы производства представлены в диапазоне ячеек B3:D3, а
количество ресурса, необходимое для производства единицы продукции, представлено в диапазонах B8:D8 для Ресурса 1, в диапазонах B9:D9 для Ресурса 2,
в диапазонах B10:D10 для Ресурса 3, то в ячейках Е8:Е10 соответственно должны быть формулы:
=СУММПРОИЗВ($B$3:$D$3;B8:D8),
=СУММПРОИЗВ($B$3:$D$3;B9:D9),
=СУММПРОИЗВ($B$3:$D$3;B10:D10),
т. е. суммы произведений соответствующих ячеек.
Рис. 3.3. Исходные данные
26
Выполним команду Данные → Поиск решения... Откроется диалоговое окно Поиск решения (рис. 3.4).
В поле Установить целевую ячейку необходимо указать $F$4.
Установить переключатель Равной: максимальному значению, что означает максимизацию значения целевой функции.
В поле Изменяя ячейки указать диапазон ячеек, в которые необходимо
будет поместить значения объемов производства для каждого вида продукции,
т.е. необходимо указать диапазон $B$3:$D$3.
Рис. 3.4. Диалоговое окно Поиск решения
В поле Ограничения: вводим ограничения для расчета, для чего необходимо нажать кнопку Добавить и в появившемся диалоговом окне заполнить
параметры ограничения для каждого неравенства.
В поле Ссылка на ячейку выбрать ячейку, содержащую формулу левой
части соответствующего неравенства, т. е. для первого неравенства выбрать
ячейку $E$8, знак ограничения ставим в соответствии с математической модели. В поле Ограничение необходимо ввести имя ячейки, содержащей значение
запасов ресурса 1, ячейку $F$8. Процедуру повторяем для каждого неравенства.
Нажимаем кнопку Параметры, откроется диалоговое окно Параметры
поиска решения. В диалоговом окне необходимо установить параметры, как показано на рис. 3.5. Нажимаем кнопку OK и возвращаемся в диалоговое окно
Поиск решения. В диалоговом окне Поиск решения нажимаем кнопку Выполнить. Если оптимальное решение существует, на экран будет выведен следующий диалог (рис. 3.6). Диалог свидетельствует об успешном поиске оптимального решения.
27
Рис. 3.5. Диалоговое окно Параметры поиска решения
Предложенное Сохранить найденное значение означает, что найденные
значения объемов производства х1, х2, х3, максимизирующие целевую функцию
прибыли будут помещены в соответствующие ячейки B3:D3.
Восстановить исходные значения – означает отмену проведенного расчета. Если решение найти не удалось, то пользователю будет выведен диалог о
неуспешной попытке поиска оптимального решения.
Результат расчета представлен на следующем рис. 3.7. Из рисунка видно,
что максимальная прибыль составит 2000 денежных единиц, при этом необходимо запланировать выпуск Продукции 2 в объеме 20 единиц, а Продукцию 2 и
Продукцию 3 не производить вовсе в условиях установленных ограничений на
использование ресурсов.
Рис. 3.6. Диалоговое окно Результат поиска решения
28
Рис. 3.7. Результат решения задачи
3.2. Задания
1. Для изготовления четырех видов продукции (П1, П2, ПЗ, П4) используются три вида ресурсов (P1, P2, Р3). Другие условия представлены в следующей таблице:
Запас ресурсов, ед.
Р1
3500
Р2
1300
Р3
3200
Прибыль от единицы
продукции, ден.ед.
Ресурсы
Нормы расхода сырья на единицу продукции, ед.
П1
П2
П3
П4
2
1
1
4
1
5
3
0
3
0
6
2
9
4
6
15
Необходимо определить план выпуска продукции, при котором прибыль
от ее реализации будет максимальной.
29
2. Для изготовления семи видов продукции (П1, П2, ПЗ, П4, П5, П6, П7)
используются пять видов ресурсов (Р1, Р2, РЗ, Р4, Р5). Другие условия представлены в следующей таблице:
Запас ресурсов, ед.
Р1
1500
Р2
3100
Р3
2300
Р4
1000
Р5
4500
Прибыль от единицы
продукции, ден.ед.
Ресурсы
Нормы расхода сырья на единицу продукции, ед.
П1
П2
П3
П4
П5
П6
П7
2
1
1
4
4
4
3
1
5
3
0
0
2
0
5
5
1
2
4
2
0
3
0
1
6
0
2
2
1
5
6
2
7
9
2
20
10
3
4
11
15
23
Необходимо определить план выпуска продукции, при котором прибыль
от ее реализации будет максимальной.
3.3. Контрольные вопросы
1. Опишите сущность задачи линейного программирования.
2. Математическая форма записи задачи линейного программирования.
3. Как математическая форма записи связывается с шаблоном для решения задачи линейного программирования?
4. Каким образом производится поиск решения задачи линейного программирования?
5. О чем говорят результаты расчета в случае успешного поиска оптимального значения?
6. Как минимизировать целевую функцию средствами Excel при заданной системе ограничений?
30
Лабораторная работа № 4
Задачи оптимальных перевозок
Цель работы:
– освоить решение задач оптимальных перевозок с помощью MS Excel;
– получить навыки использования транспортных задач в
хозяйственной деятельности современных предприятий
и организаций.
4.1. Основные сведения
Общая постановка задачи оптимальных перевозок (транспортной задачи)
состоит в определении оптимального плана перевозок некоторого однородного
груза из т пунктов отправления А1, А2, ..., Аm в п пунктов назначения В1, В2, ..., Вn.
В качестве критерия оптимальности (целевая функция) обычно задается
минимальная суммарная стоимость перевозок всего груза или минимальная
суммарная транспортная работа по доставке грузов, которая может быть пропорциональна времени доставки грузов потребителям или расстоянию между
поставщиками и потребителями. Рассмотрим транспортную задачу, в качестве
критерия оптимальности которой взята минимальная суммарная стоимость перевозок всего груза [3, 5, 6].
Обозначим сij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через ai – запасы груза в i-м пункте отправления,
через bj – потребности в грузе в j-м пункте назначения, а через xij – количество
единиц груза, перевозимого из i-o пункта отправления в j-й пункт назначения.
Тогда математическая модель транспортной задачи состоит в определении минимального значения функции:
F
m n
cij xij min ,
(4.1)
i 1 j 1
при условиях
m
xij b j ,
j 1, 2, , n
xij ai ,
i 1, 2, , m
i 1
n
(4.2)
j 1
xij 0, i 1, 2, m; j 1, 2, n.
Поскольку переменные xij 0, i 1, 2,m; j 1, 2,n удовлетворяют системам линейных уравнений и условию неотрицательности (4.2), обеспечиваются
доставка необходимого количества груза в каждый из пунктов назначения, вывоз всего имеющегося груза из всех пунктов отправления, а также исключаются
обратные перевозки.
31
Суммарное количество груза у поставщиков равно
m
a
i 1
требность в грузе в пунктах назначения равна
n
b
j 1
j
i
, а суммарная по-
единиц. Если суммарная
потребность в грузе в пунктах назначения равна суммарному запасу груза в
пунктах отправления, т. е.
m
n
i 1
j 1
ai b j ,
(4.3)
то такая транспортная задача называется закрытой или сбалансированной. В
противном случае – открытой или несбалансированной.
В случае превышения суммарного запаса над суммарной потребностью,
т. е. если
m
n
i 1
j 1
ai b j ,
вводится фиктивный n+1-й потребитель (или пункт назначения) с потребностью, равной:
m
n
i 1
j 1
bn1 ai b j ,
а соответствующие транспортные тарифы от всех поставщиков до фиктивного
потребителя полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (4.3).
В случае превышения суммарной потребности в грузе над суммарными
запасами поставщиков, т. е. если
m
n
i 1
j 1
ai b j ,
вводится фиктивный m+1-й пункт отправления с запасом груза в нем, равным:
n
m
j 1
i 1
a m1 b j ai ,
а соответствующие транспортные тарифы от фиктивного поставщика до всех
потребителей полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (4.3).
Замечания.
1.
Перед решением транспортной задачи необходимо сначала проверить, является ли транспортная задача открытой или закрытой. Если транспортная задача является открытой, то необходимо ввести фиктивного поставщика или фиктивного потребителя.
2.
Оптимальное решение транспортной задачи при целочисленных
правых частях ограничений всегда является целочисленным.
m
3.
n
В целевой функции F cij xij min коэффициенты cij могут
i 1 j 1
быть как тарифами, так и расстояниями между пунктами отправления и получения грузов или временами доставки грузов. В двух последних случаях целевая функция представляет собой транспортную работу.
32
Рассмотрим решение транспортной задача на следующем примере.
Предположим необходимо организовать поставки сырья на 5 заводов города Владикавказ. На заводах спрос на сырье равен соответственно 500 ед., 600 ед.,
500 ед., 5000 ед. и 1000 ед. Сырье сосредоточено у четырех поставщиков на складах в разных городах, запасы которых равны 750 ед., 900 ед. 4500 ед. и 550 ед.
Сырье на заводы может завозиться от любого поставщика. Стоимость перевозки единицы сырья cij (i – номер поставщика, j – номер завода-потребителя) известны и задаются матрицей:
2
3
С
4
2
3 4 8 5
4 6 2 7
.
6 8 2 6
5 5 4 3
Составить такой план перевозок, при котором суммарная стоимость всех
перевозок будет минимальной.
Математическая модель. Обозначим через хij количество единиц сырья,
перевозимого от i-гo поставщика на j-й завод. Так как сумма запасов грузов
750 + 900 + 4500 + 550 = 6700 поставщиков не равна сумме потребностей грузов потребителей: 500 + 600 + 500 + 5000 + 1000 = 7600. Таким образом, потребности в грузах у потребителей превышают их запасы у поставщиков и
данная транспортная задача является открытой. Для того чтобы она стала закрытой, вводим фиктивного поставщика с номером 5, у которого запас груза
равен 7600 – 6700 = 900 ед. В этом случае суммарный запас у поставщиков
станет равным 7600 и мы получим закрытую транспортную задачу. При этом
все тарифы от фиктивного поставщика ко всем потребителям груза полагаются
равными нулю. В матрице тарифов появится пятая строка, в которой стоят все
нули:
2
3
С 4
2
0
3
4
6
5
0
4
6
8
5
0
8
2
2
4
0
5
7
6.
3
0
Условия доставки необходимого сырья и вывоза имеющегося сырья
обеспечиваются выполнением следующих равенств-ограничений:
х11 х12 х13 х14 х15 750,
х х х х х 900,
22
23
24
25
21
х31 х32 х33 х34 х35 4900 ,
х х х х х 550,
42
43
44
45
41
х51 х52 х53 х54 х55 900,
33
(4.4)
х11 х21 х31 х41 х51 500,
х х х х х 600,
22
32
42
52
12
х13 х23 х33 х43 х53 500,
х х х х х 5000 ,
24
34
44
54
14
х15 х25 х35 х45 х55 1000 .
xij 0, i 1,5;
(4.5)
j 1,5
Целевая функция, выражающая суммарную стоимость перевозок, при
данном плане составит:
F 2 x11 3 x12 4 x13 8 x14 5 x15 3 x21 4 x22 6 x23
2 x24 7 x25 4 x31 6 x32 8 x33 2 x34 6 x35 2 x41 5 x42
(4.6)
5 x43 4 x4 5 x15 0 x51 0 x52 0 x53 0 x54 0 x55 min
Таким образом, математическая постановка задачи состоит в нахождении
такого неотрицательного решения системы линейных равенств-ограничений (4.4)
и (4.5), при котором целевая функция (4.6) принимает минимальное значение.
Решение задачи средствами Excel.
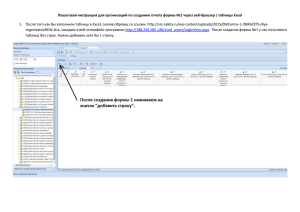
Создаем рабочую форму на чистом листе книги Excel (рис. 4.1).
Рис. 4.1. Создание рабочей формы для решения транспортной задачи
34
В ячейках B4:B8 заносим запасы грузов, хранящиеся на складах у поставщиков, включая и фиктивного поставщика, в ячейках E4:E8 заносим потребности в сырье на заводах. В ячейки с адресами B15:F19 занесены коэффициенты матрицы стоимости на перевозку сырья между всеми пунктами отправления и назначения. Пятая строка этой матрицы соответствует (ячейки
B19:F19) перевозкам от фиктивного поставщика.
В ячейки G26:G30 введем формулы для расчета ограничений (4.4), а в
ячейки B31:F31 – формулы для расчета ограничений (4.5).
Формулу для расчета целевой функции вводим в ячейку I21 и имеет следующий вид:
=СУММПРОИЗВ(B15:F19;B26:F30).
Выполним команду Сервис→Поиск решения... Откроется диалоговое окно
Поиск решения. В поле Установить целевую ячейку необходимо указать $I$21.
Установить переключатель Равной: минимальному значению, что означает минимизацию значения целевой функции.
В поле Изменяя ячейки указать диапазон ячеек, в которые необходимо
будет поместить значения объемов производства для каждого вида продукции,
т.е. необходимо указать диапазон $B$26:$F$30.
В поле Ограничения: вводим ограничения для расчета, для чего необходимо нажать кнопку Добавить и в появившемся диалоговом окне заполнить
ограничения
для
каждого
равенства
($B$31:$F$31=$E$4:$E$8,
$G$26:$G$30=$B$4:$B$8, $B$26:$F$30=целое и $B$26:$F$30>=0). Диалоговое
окно Поиск решения будет выглядеть, как на рис. 4.2.
Рис. 4.2. Диалоговое окно Поиск решения с занесенными данными
В диалоговом окне Поиск решения нажимаем кнопку Выполнить. Если
оптимальное решение существует, на экран будет выведен следующий диалог,
свидетельствующий об успешном поиске оптимального решения.
Предложенное Сохранить найденное значение означает, что найденные
оптимальные значения по стоимости перевозок в заданной системе ограничений, минимзирующие целевую функцию будут помещены в соответствующие
ячейки $B$26:$F$30.
35
Восстановить исходные значения – означает отмену проведенного расчета. Если решение найти не удалось, то пользователю будет выведен диалог о
неуспешной попытке поиска оптимального решения.
Результат расчета представлен на следующем рис. 4.3. Из рисунка видно,
что суммарная минимальная стоимость всех перевозок составит 15 050 денежных единиц.
Рис. 4.3. Результат решения транспортной задачи
Полученный результат позволяет сделать вывод, что сырье от Поставщика 1
надо вести сырье на Завод 1 (х11) в количестве 194 ед., на Завод 2 (х12) – 506 ед. и
на Завод 3 (х13) – 50 ед. От Поставщика 2 надо вести сырье на Завод 1 (х21) в
количестве 306 ед., на Завод 2 (х22) – 94 ед. и на Завод 4 (х24) – 500 ед. Поставщик 3 все сырье отправляет на Завод 4 (х34) – 4500 ед. Поставщик 4 все сырье
отправляет на Завод 5 (х45) – 550 ед. От фиктивного Поставщика 5 на Завод 3
(х53) в количестве 450 ед. и на Завод 5 (х55) – 450 ед.
Переменные х14 = х15 = х23 = х25 = х31 = х32 = х33 = х35 = х41 = х42 = х43 =
=х44 = х51 = х52 = х54.
36
4.2. Задания
1. Продукты, находящиеся на четырех складах – C1, С2, СЗ, С4, необходимо развезти по пяти магазинам – M1, М2, МЗ, М4 и М5. Потребности этих
магазинов в продуктах равны соответственно 15, 14, 25, 5 и 9 ед. Запасы продуктов на складах С1, С2, СЗ, С4 составляют соответственно 23, 15, 45, 15 ед.
Тарифы по доставке продуктов (руб./ед. груза) приведены в таблице:
Магазины
Склады
М1
М2
М3
М4
М5
С1
10
3
4
5
3
С2
2
1
11
14
5
С3
4
13
3
2
8
С4
5
13
4
12
3
Составьте план перевозок продуктов, при котором суммарные расходы по
их доставке будут минимальными.
2. Зерно, находящееся на четырех элеваторах – Э1, Э2, ЭЗ, Э4, необходимо доставить на пять сельскохозяйственных предприятий для посева – СХП1,
СХП2, СХПЗ, СХП4 и СХП5. Потребности в зерне сельскохозяйственных предприятий равны соответственно 100, 70, 30, 45 и 50 т. Запасы зерна на элеваторах Э1, Э2, ЭЗ, Э4 составляют соответственно 54, 32, 85, 162 т. Стоимость доставки 1 т зерна (руб./т) приведена в таблице:
Магазины
Элеваторы
СХП1
СХП2
СХП3
СХП4
СХП5
Э1
12
14
32
20
3
Э2
8
10
12
24
12
Э3
6
8
12
24
8
Э4
10
18
4
8
9
Составьте оптимальный план перевозок зерна, при котором суммарные
расходы по его доставке будут минимальными.
3. Груз, находящийся на четырех складах – 1, 2, 3, 4 – необходимо доставить пяти потребителям – 1, 2, 3, 4 и 5. Потребность в грузе этих потребителей
составляет, соответственно, 15, 10, 25, 5 и 9 т. Запасы груза на складах 1, 2, 3, 4
составляют, соответственно, 20, 15, 40, 15 т. Стоимость доставки 1 т груза задается матрицей (руб./т):
1
2
C
1
3
3 4 5 2
1 1 4 5
.
3 3 2 1
1 4 2 3
Составьте оптимальный план перевозок груза, при котором суммарные
расходы будут минимальными.
4.
В области имеется три кирпичных завода – 1, 2 и 3, объем выпуска
которых в сутки равен 60, 30 и 40 т. Заводы удовлетворяют потребность в кирпиче пяти строительных фирм – 1, 2, 3, 4 и 5 в количестве, соответственно рав37
ном 10, 20, 40, 30 и 65 т. Стоимость перевозок 1 т кирпича (р./т) с заводов на
фирмы задается матрицей:
10 8 3 15 16
С 7 5 9 4 6 .
2 0 14 5 20
Определите, с каких заводов, на какие фирмы и в каких объемах необходимо доставлять кирпич, чтобы суммарная стоимость перевозок была минимальной.
5.
Для строительства пяти участков дороги необходимо завозить песок. Песок может быть доставлен из четырех карьеров. Расстояния от карьеров
до участков дороги, а также объемы песка в карьерах и потребность в песке на
каждом участке дороги приведены в таблице:
Расстояние от карьеров до разОбъем песка в
личных участков дороги, км.
Карьеры
карьерах, тыс.т.
1
2
3
4
5
1
3
7
3
4
0
50
2
6
2
5
7
4
55
3
8
5
8
3
4
60
4
1
3
6
5
3
20
Потребность в песке на
30
60
40
20
15
участках дороги, тыс.т.
Перевозка песка из карьеров на различные участки дороги осуществляется грузовиками одинаковой грузоподъемности. Составьте план перевозок песка,
минимизирующий суммарную транспортную работу, равную сумме (по всем
поставщикам и потребителям) произведений {проходимого грузовиками расстояния}*{объемов соответствующих поставок груза}.
4.3. Контрольные вопросы
1. Приведите математическую модель транспортной задачи.
2. Каков смысл целевой функции в транспортной задаче? Какие критерии оптимальности перевозок может выражать целевая функция?
3. Раскройте понятия закрытой и открытой транспортной задач.
4. Как необходимо скорректировать математическую модель транспортной задачи, если суммарный запас груза у поставщиков больше, чем спрос на
груз у потребителей?
5. Что такое фиктивные поставщики и фиктивные потребители и в каких
случаях они вводятся в транспортную модель?
6. Как определяется транспортная работа по доставке грузов, если коэффициенты cij в целевой функции представляют собой:
а) время доставки грузов;
б) расстояния от поставщиков до потребителей грузов?
7. Как в Excel задаются ограничения и целевая функция транспортной
задачи?
38
Рекомендуемая литература
1. Основы современных компьютерных технологий: Учебник / Г. А. Брякалов, С. В. Войцеховский и др.; Под ред. А. Д. Хомоненко. СПб.: КОРОНА
принт, 2005. 672 с.
2. Описание технологии использования программы Excel – справочная
система программы.
3. Дубина А. Г., Орлова С. С., Шубина И. Ю., Хромов А. В. Excel для экономистов и менеджеров. СПб.: Питер, 2004. 295 с.
4. Гарнаев А. Ю. Excel, VBA, Internet в экономике и финансах. СПб.:
БХВ-Петербург, 2005. 816 с.
5. Мадера А. Г. Математические модели в управлении: Компьютерное
моделирование в Excel: Лабораторные работы. М.: РГГУ, 2007. 118 с.
6. Информационные технологии в экономике: практикум (Часть 1) / Г. Г. Арунянц, А. Ю. Калинкин, Д. Н. Столбовский; Под ред. Г. Г. Арунянца, К. Х. Пагиева. Владикавказ: Олимп, 2001. 600 с.
39
Оглавление
Организация и методические указания
по выполнению лабораторных работ ..................................................................... 3
Лабораторная работа № 1.
Решение финансовых задач с помощью MS Excel ............................................... 4
1.1. Функции MS Excel .................................................................................. 4
1.2. Некоторые часто используемые финансовые функции ...................... 5
1.3. Аргументы финансовых функций ......................................................... 5
1.4. Примеры решения задач с использованием
финансовых функций Excel .......................................................................... 6
1.5. 3адачи для самостоятельного решения................................................ 12
1.6. Задания .................................................................................................... 13
1.7. Контрольные вопросы ........................................................................... 14
Лабораторная работа № 2. Решение и анализ
финансово-экономических задач средствами MS Excel ..................................... 15
2.1. Подбор параметра .................................................................................. 15
2.2. Сценарий ................................................................................................. 17
2.3. Задания .................................................................................................... 20
2.4. Контрольные вопросы ........................................................................... 21
Лабораторная работа № 3. Задачи линейного программирования ................. 22
3.1. Основные сведения ................................................................................ 22
3.2. Задания .................................................................................................... 29
3.3. Контрольные вопросы ........................................................................... 30
Лабораторная работа № 4. Задачи оптимальных перевозок ............................ 31
4.1. Основные сведения ................................................................................ 31
4.2. Задания .................................................................................................... 37
4.3. Контрольные вопросы ........................................................................... 38
Рекомендуемая литература ..................................................................................... 39
40