Акмулла 2016 физика

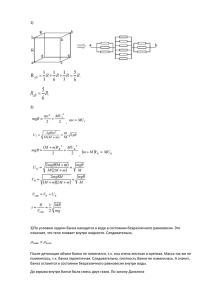
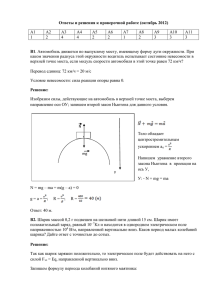
Задание 6: Применяя закон отражения, построим изображение экрана (A1B1) в зеркале (см.
рисунок). Вертикальной штриховкой отмечена область, откуда можно видеть в зеркале отражение
точки А; горизонтальной штриховкой — соответствующая область для точки В. Из области,
отмеченной двойной штриховкой, можно видеть отражения точек А и Б, а, значит, и всего экрана
телевизора.
Ответ: Искомая область заштрихованна (область, из любой точки которой будет видно все
изображение экрана) отмечена двойной штриховкой.
Задание 7: Систему отсчета, связанную с горкой можно считать инерциальной (поверхности
гладкие, горка массивная). Начальная скорость шайбы относительно горки равна (v + u). По закону
сохранения энергии: + mgH. Отсюда скорость шайбы в точке С: . Для определения силы давления
шайбы на горку в точке С, расставляем силы, действующие на шайбу, записываем уравнение
движения для шайбы в точке С (2-й закон Ньютона) в проекциях на радиальное направление. N =
(m/4)·(5g – (v + u)2/H). N - сила реакции горки. В соответствии с 3-м законом Ньютона шайба давит
на горку с такой же силой, но в обратном направлении.
Рассмотрим момент, когда шарик скатился с трамплина, но еще не ударился о тележку.
Применяем закон сохранения энергии и закон сохранения импульса для системы шарик и
трамплин:
Задание 2:Рассмотрим момент, когда шарик скатился с трамплина, но еще не ударился о
тележку. Применяем закон сохранения энергии и закон сохранения импульса для системы шарик и
трамплин:
,
Решая систему этих уравнений, находим скорость трамплина сразу после первоначального
скатывания с него шарика. Кроме того, учитывая, что m << M, то можно заменить (m + M) на M.
Т.к. шарик с тележки не упал, то конечные скорости шарика и тележки равны. Применяем закон
сохранения энергии и закон сохранения импульса для системы шарик, трамплин и тележка в
конечный момент времени перед падением трамплина с тележки:
,
Решая систему этих уравнений, находим конечные скорости тележки и трамплина. Снова
учитываем, что m << M:
Т.о. получилось, что эти скорости приблизительно одинаковы. Тогда скорость трамплина
относительно датчика-таймера равна
Находим время движения, т.е. показания датчика-таймера:
Задание 3:По условию задачи банка находится в воде в состоянии безразличного
равновесия. Это означает, что тело плавает внутри жидкости. Следовательно,
После детонации объем банки не поменялся, т.к. она очень жесткая и крепкая. Масса так же не
поменялась, т.к. банка герметичная. Следовательно, плотность банки не изменилась. А значит,
банка останется в состоянии безразличного равновесия внутри воды.
До взрыва внутри банки была смесь двух газов. По закону Дальтона
При взрыве образуется вода из одного атома кислорода и двух атомов водорода. Следовательно,
при взрыве израсходуется половина молекул кислорода, а молекул воды станет столько же,
сколько было молекул водорода. Тогда
По закону Дальтона для смеси газов через длительный промежуток времени после взрыва будет
давление
Применим уравнение Менделеева-Клайперона для состояния до и после взрыва:
Т.о. даже если через длительное время все молекулы воды будут находиться в газообразном
состоянии, то все равно начальное давление больше конечного.
Рассмотрим теперь случай, когда давление газов внутри банки через длительный промежуток
времени после взрыва стало в 2 раза меньше первоначального. Применим уравнение МенделееваКлайперона:
Это означает, что половина воды сконденсировалась. Вторая половина воды в виде насыщенного
пара давит на стенки сосуда, причем при стоградусной температуре давление насыщенных паров
воды равно атмосферному. Из уравнения Менделеева-Клайперона для насыщенного пара найдем
первоначальное количество вещества одного из газов:
При подстановке получаем, что начальное давление равно 4 · 105 Па.
Задание 5: Для охлаждения воды на ΔT1 = 16ºС - 4ºС = 12ºС от неѐ было отведено количество
тепла, равное Q1 = сmΔT1. Будем считать, что морозильник работает непрерывно и скорость
отвода тепла в нем постоянна. По условиям задачи известно время охлаждения воды, поэтому
можно рассчитать скорость теплоотвода: q = Q1/ t1 = сmΔT1/ t1. Тогда время t2, необходимое для
дальнейшего охлаждения воды от 4ºС до 0ºС, т.е. на ΔT2 = 4ºС, будет равно t2 = Q2/q = сmΔT2t1 /
сmΔT1 = t1 ΔT2/ ΔT1. Подставив численные значения, получим t2 = 5 мин, а время t3 необходимое
для превращения в лед всей воды, находящейся при 0ºС, составит t3 = Q3/q = mλ t1/ сmΔT1 = λ t1/
сΔT1. t3 =100 мин. Таким образом, время необходимое для приготовления льда, от момента
постановки воды в морозильник до ее полного замерзания составит t = t1 + t2 + t3 = 120 мин = 2 ч.
Ответ. Вода не успеет замерзнуть к Новому году, а замерзнет 1 января в 1 час 00 мин.
Задание 4:
U1 = I1r
Напряжения, которые показывают вольтметры:
U2 = I2r U3 = I¢2r,
где
. (1)
Но из рисунка видно, что U1 = I¢1r + U2 U2 = I¢2r + U3.
Отсюда
; (2)
. (3)
В выражениях (1) и (3) приравняем правые части.
=
. (4)
По закону Кирхгофа:
I¢1 = I2 + I¢2 =
+
=
. (5)
Приравняем правые части (2) и (5).
=
. (6)
Поделим четвертое уравнение на шестое.
×
=
×
,
.
Подставим численные значения и произведем вычисления.
- 64 = 8(10 – U2),
+ 8U2 - 144 = 0.
= 8,6 (В).
Ответ: U2 = 8,6 В