9 - Faik.Az

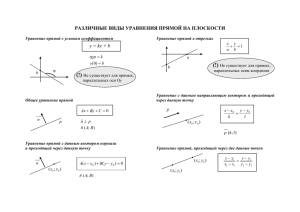
ТЕМА IV. УРАВНЕНИЕ ЛИНИИ И ПЛОСКОСТИ.
ЛЕКЦИЯ 9. Уравнение прямой на плоскости.
Уравнение прямой с угловым коэффициентом.
Пусть дана некоторая прямая L . Углом наклона прямой L к оси Ox называется
угол  , отсчитываемый от положительного направления оси до прямой L против
движения часовой стрелки (рис. 1). Если прямая параллельна оси Ox , то полагают   0 .
Таким образом, угол наклона  удовлетворяет неравенству 0     .
Рис. 1. Линии первого порядка.
Угловым коэффициентом прямой называется число, равное тангенсу угла наклона
прямой к оси Ox :
k  tg
(1)
Из формулы (1), в частности, следует, что если   0 , т.е. прямая параллельна оси
Ox , то k  0 . Если    / 2 , т.е. прямая перпендикулярна оси Ox , то формула (1) теряет
смысл. В таком случае говорят, что угловой коэффициент обращается в бесконечность.
Выведем уравнение данной прямой, если известны её угловой коэффициент k и
величина b отрезка OB , который она отсекает на оси Oy (рис. 1).
Обозначим через M произвольную точку плоскости с координатами x и y . Если
провести прямые BN и MN , параллельные осям координат, то в случае k  0 образуется
прямоугольный треугольник BNM . Точка M лежит на прямой тогда и только тогда,
когда величина MN и BN удовлетворяют условию:
NM
 tg
BN
120
Но NM  CM  CN  y  b , BN  x . Отсюда, учитывая формулу (1), получаем, что
точка M x; y  лежит на прямой L тогда и только тогда, когда ее координаты
удовлетворяют уравнению
y b
k
x
Это уравнение после преобразования принимает вид:
y  kx  b
(2)
Уравнение (2) называется уравнением прямой с угловым коэффициентом (dцз
хятин бужаг ямсаллы тянлийи).
Частные случаи:
1. b  0 , k  0 . Прямая, определяемая уравнением y  kx , проходит через начало
координат;
2. k  0 , b  0 . Прямая, определяемая уравнением y  b , параллельна оси Ox ;
3. k  0 , b  0 . Прямая, определяемая уравнением y  0 , совпадает с осью Ox .
Уравнение прямой, проходящей через данную точку, с данным угловым
коэффициентом.
В ряде случаев возникает необходимость составления уравнения прямой, зная
координату одной её точки M1 x1 ; y1  и угловой коэффициент k . Запишем уравнение
прямой в виде (2), где b , пока неизвестное число. Так как прямая проходит через точку
M1 x1 ; y1  , то координаты этой точки удовлетворяют уравнению (2): y1  kx1  b . Отсюда
b  y1  kx1 . Подставляя это в уравнение (2), получаем искомое уравнение прямой:
y  y1  k x  x1 
(3)
Уравнение прямой, проходящей через две данные точки.
Приняв в (3) точку M x; y  за M 2 x2 ; y 2 , получим: y2  y1  k x2  x1  . Если
x2  x1 , то, определяя k из последнего равенства и подставляя его в уравнение (3),
получаем искомое уравнение прямой:
x  x1
y  y1

x 2  x1 y 2  y1
(4)
121
Если y1  y 2 , то уравнение искомой прямой имеет вид y  y1 , и такая прямая
параллельна оси Ox . Если x1  x2 , то прямая, проходящая через точки M1 x1 ; y1  и
M 2 x2 ; y2  , параллельна оси Oy , ее уравнение имеет вид x  x1 .
Общее уравнение прямой. Неполные уравнения первой степени. Уравнение прямой
«в отрезках».
В прямоугольной системе координат любая прямая задается уравнением первой
степени
Ax  By  C  0
Рассмотрим три частных случая, когда уравнение
(5)
Ax  By  C  0 является
неполным, т.е. один из коэффициентов равен нулю.
1) C = 0; уравнение имеет вид Ax  By  0 и определяет прямую, проходящую через
начало координат;
2) B = 0 (A ≠ 0); уравнение имеет вид Ax  C  0 и определяет прямую, параллельную оси
Oy . В частности, уравнение x = 0 определяет ось ординат;
3) A = 0 (B ≠ 0); уравнение имеет вид By  C  0 и определяет прямую, параллельную оси
Ox . В частности, уравнение y = 0 определяет ось абсцисс.
Рассмотрим теперь уравнение Ax  By  C  0 при условии, что ни один из
коэффициентов А, В, С не равен нулю. Преобразуем его к виду:
x
y

1
C
C


A
B
Введя обозначения a  
C
C
, b   , получаем
A
B
x y
 1
a b
(6)
122
Уравнение (6) называется уравнением прямой «в отрезках». Числа а и b являются
величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения
удобна для геометрического построения прямой.
Пример. Прямая задана уравнением 2 x  3 y  6  0 . Составить для этой прямой уравнение
«в отрезках» и построить прямую.
Решение. Для данной прямой уравнение «в отрезках» имеет вид:
x
y
 1
3 2
Чтобы построить эту прямую, отложим на осях координат Ox и Oy отрезки,
величины которых соответственно равны a  3 , b  2 , и проведем прямую через точки
M 1  3;0 и M 2 0;2 (рис. 2).
Рис. 2.
Нормальное (полярное) уравнение прямой.
Пусть дана некоторая прямая L (рис. 3). Проведем через начало координат
прямую, перпендикулярную к данной и назовем её нормалью к прямой L . Буква N
означает точку, в которой нормаль пересекает прямую
L . На нормали введем
направление от точки О к точке N . Таким образом, нормаль станет осью. Из рисунка
видно, что 0    2 , p  0 . Выведем уравнение данной прямой, считая известными
числа  и p . Для этого возьмем на прямой произвольную точку M с координатами
; .
Из треугольника ONM имеем:
p   cos      cos  cos   sin  sin   или
 cos  cos    sin  sin   p  0
(7)
Уравнение (7) – уравнение прямой L в полярных координатах. Так как  cos   x ,
 sin   y , то в прямоугольной системе координат (7) принимает вид:
x cos   y sin   p  0
(8)
123
Уравнение (8) называется нормальным уравнением прямой.
Рис. 3.
Покажем, как привести уравнение (5) прямой к виду (8). Умножим все члены
уравнения (5) на некоторый множитель   0 . Получим Ax  By  C  0 . Это
уравнение должно обратиться в уравнение (10). Следовательно, должны выполняться
равенства:
A  cos  , B  sin  , C   p . Из первых двух равенств находим
2 A 2  2 B 2  cos 2   sin 2  , т.е.

Множитель 
1
(9)
A2  B 2
называется нормирующим множителем. Согласно третьему
равенству C   p знак нормирующего множителя противоположен знаку свободного
члена C общего уравнения прямой.
Пример. Привести уравнение  3x  4 y  15  0 к нормальному виду.
Решение. Находим нормирующий множитель   
1
1
  . Умножая данное
5
 3  4
2
2
уравнение на  , получаем искомое нормальное уравнение прямой:
3
4
x y 3  0
5
5
124
СЕМИНАР 9.
Пример 1. Даны точки A0;2 , B 2;1 , C0;0 и D2;9 . Укажите те из них, которые
лежат на прямой 2 x  3 y  7  0 .
Решение. Уравнению прямой удовлетворяют координаты только точки B .
Пример 2. Составить уравнение прямой, отсекающей на оси ординат отрезок b  3 и
образующей с положительным направлением оси абсцисс угол    / 6 .
Решение. Найдем угловой коэффициент k  tg
имеющиеся значения k 
1
3

6
и b  3 , получим y 

1
1
x 3.
3
3
. Подставив в уравнение (2)
Пример 3. Составить уравнение прямой, отсекающей на оси Oy отрезок b  2 и
образующей с осью Ox угол    / 3 .
Решение. Находим угловой коэффициент: k  tg  tg

3
 3 . Подставляя k и b в
уравнение (2), получаем искомое уравнение прямой:
y  3 x  2 или y  3 x  2  0
Пример 4. Построить прямую, заданную уравнением y 
3
x2.
4
Решение. Отложим на оси Oy отрезок OB , величина которого равна 2 (см. рисунок).
Рисунок к примеру 4.
Проведем через точку B параллельно оси Ox отрезок, величина которого BN  4
и через точку N параллельно оси Oy отрезок, величина которого NM  3 . Затем
проведем прямую BM , которая является искомой. Она имеет угловой коэффициент
k  3 / 4 и отсекает на оси Oy отрезок величины b  2 .
125
Пример 5. Провести прямую, проходящую через точки В (5;1) , С (3;4) .
Решение. Подставим координаты точек В и С в уравнение (3):
x5
y 1

, т.е.
3  5  4 1
x  5 y 1
.

2
5
Пример 6. Составить уравнение прямой, проходящей через точку M 1;2 и образующей с
осью Ox угол    / 4 .
Решение. Находим угловой коэффициент: k  tg  tg

4
 1 . Подставляя k и данные
координаты в уравнение (3), получаем искомое уравнение прямой:
y  2  x  1 или y  x  1  0
Пример 7. Составить уравнение прямой линии, образующей с осью OX угол 60° и
пересекающей ось OY в точке 0,2 . Выяснить, проходит ли эта прямая через точки
 
A 3 ,1 и B2,5 .
Решение. Из условия задачи следует, что начальная ордината
b  2 , угловой
коэффициент k  tg 60  3 , следовательно, по формуле y  kx  b имеем y  x 3  2 .
Подставляя в искомое уравнение прямой координаты точки A вместо текущих координат,
 
получим 1  3  2 , т.е. 1=1. Прямая проходит через точку A 3 ,1 . Аналогично, подставляя
в уравнение координаты точки B , получим: 5  3  2 . Прямая не проходит через точку
B.
Пример 8. Дано общее уравнение прямой 2 x  3 y  6  0 . Составим уравнение этой
прямой с угловым коэффициентом и уравнение в отрезках.
Решение.
1. Так как прямая не параллельна оси OY (B = 3 ≠ 0), можно разрешить уравнение
2
относительно y. Получаем y   x  2 . Угловой коэффициент k=−2/3.
3
2. Так как прямая пересекает обе оси и не проходит через начало координат ( A  2  0 ,
B  3  0 , C  6  0 ), преобразуем уравнение к виду
x y
  1 . Отрезки, отсекаемые
3 2
прямой на осях координат: a  3 , b  2 .
Пример 9. Составим уравнение прямой с угловым коэффициентом k=−1, проходящей
через точку M(2, −3).
Решение.
1. Уравнение прямой с k=−1 имеет вид: y   x  b .
126
2. Подставляя в уравнение y   x  b координаты точки M ( x  2 и y  3 ), получаем
уравнение относительно b: −3 = −2 + b. Отсюда b = −1.
Ответ: уравнение прямой x  y  1  0 .
Пример 10. Составим уравнение прямой, проходящей через точки M 1 0;1 ) и M 2 2;1 .
Решение.
1. Уравнение прямой проходящей через две точки имеет вид:
x  x1
y  y1

x 2  x1 y 2  y1
2. Подставляя координаты точек x1  0 , y1  1 , и x2  2 , y 2  1 , получаем
x y 1
или

2
2
x  y 1  0 .
Проверка. Подставляя в полученное уравнение координаты обеих точек, получаем
тождества. Ответ: уравнение прямой x  y  1  0 .
Пример 11. Написать уравнение прямой, проходящей через данные точки A2;5 и B1;3 .
Решение. Используя формулу
y  y1
x  x1

запишем уравнение данной прямой
y2  y1 x2  x1
y  (5) x  2
y5


 ( x  2)  8 x  y  11  0
3  (5) 1  2
8
.
Пример 12. Получить уравнение прямой, проходящей через точки M 1 3;1 и M 2 5;4 .
Представить эскиз.
Решение. По условию: x1  3 , y1  1 , x2  5 , y 2  4 .
Тогда
y 1 x  3
y 1 x  3
7 3



 2 y  2  3x  9  y     x .
4 1 5  3
3
2
2 2
Получаем ответ на
первую часть задачи – уравнение прямой имеет вид y   7  3  В силу чего, получаем
2
эскиз: ось Oy пересекается в точке 
2
7
, а эскиз – на рисунке
2
127
Пример 13.Две прямые заданы своими уравнениями: 1) y  3  10 x
и
2) y  3  2 x .
Какая из данных прямых возрастает быстрее и почему? Представить эскиз обеих прямых.
Решение. Быстрее возрастает прямая 1), потому что ее угловой коэффициент (10) больше,
чем угловой коэффициент примой 2) (2). Эскиз прямых представлен на рисунке.
Пример 14. Найти уравнение диагонали BD параллелограмма ABCD как уравнение
прямой, проходящей через точки B (5;1) и E , где E - середина отрезка AC .
Решение. Так как точка пересечения диагоналей является их серединой, то точка E
(середина отрезка АС ) является точкой пересечения диагоналей и диагональ BD
проходит через точку E . Если А( x1 ; y1 ) и C( x2 ; y2 ) , то координаты точки Е ( x0 ; y0 ) середины отрезка
AC , определяются формулами
A( 2;3) , C (3;4) . В силу формул имеем: x0 
x0 
x1  x2
y  y2
, y0  1
. Пусть
2
2
23 5
34
7
 , y0 
  . Следовательно
2
2
2
2
5 7
5 7
E ( ; ) . По условию B (5;1) , E ( ; ) . Тогда уравнение прямой BE (диагонали BD )
2 2
2 2
имеет вид:
x5
y 1
x  5 y 1
или
. Запишем это уравнение в общем виде:


5
7
5
9
 5  1


2
2
2
2
9 x  5 y  40  0 . Запишем это же уравнение в виде с угловым коэффициентом: y 
9
x 8.
5
Пример 15. Записать уравнение прямой, проходящей через точки M 1 2;3 и M 2 1;0 (см.
рисунок).
128
Решение. Напишем уравнение уравнение прямой, проходящей через точки M 1 2;3 и
M 2 1;0 :
х  2 у 1

, отсюда получаем: После раскрытия скобок и приведения подобных
1 2 0  3
слагаемых получим общее уравнение прямой: 3x  y  3  0 .
Пример 16. Дано общее уравнение прямой: 3 x  3 y  10  0 . Найти отрезок, отсекаемый
этой прямой от оси Oy и угол между прямой и осью Ox .
Решение. Решим данное уравнение относительно переменной y , получим: y   x  10 / 3
– уравнение прямой с угловым коэффициентом k = tg  = –1 и начальной ординатой b =
10/3. Значит, прямая проходит через точку M 1 0;10 / 3 и составляет с осью Ox угол
  3 / 4 .
129
ЛЕКЦИЯ 10. Расстояние от точки до прямой. Взаимное расположений прямых на
плоскости.
Расстояние от точки до прямой.
С помощью уравнения (8) можно определить расстояние d от данной точки
M 0 ( x0 ; y0 ) до прямой L .
Проведем через точку M 0 ( x0 ; y0 ) прямую L0 , параллельную L . Пусть N 0 - точка
пересечения L0 с нормалью n к прямой, p 0 - длина ON 0 (рис. 4).
Рис. 4.
Если точки N и N 0 лежат по одну сторону от точки O , то нормальное
уравнение
L0
имеет
вид
x cos   y sin   p0  0 .
Т.к.
M 0  L0 ,
то
x0 cos   y0 sin   p0  0 . Следовательно, p0  x0 cos   y0 sin  и
d  p0  p  x0 cos   y0 sin   p
Если N и N 0 лежат по разные стороны от точки O , то нормальное уравнение L0
имеет
вид
x cos 1  y sin 1  p0  0 ,
где
1     .
Следовательно,
p0  x0 cos 1  y0 sin 1   x0 cos   y0 sin  или
d  p0  p   x0 cos   y0 sin   p = d  x0 cos   y0 sin   p
Поэтому получаем
d  x0 cos   y0 sin   p
(1)
Если прямая задана уравнением Ax  By  C  0 , то с помощью нормирующего
множителя   
1
A2  B 2
, сделав замену в (1) cos   A , sin   B ,  p  C
130
получим, что расстояние d от данной точки M 0 ( x0 ; y0 ) до прямой L определяется
формулой:
Ax0  By 0  C
d
(2)
A2  B 2
Угол между двумя прямыми.
Пусть прямые L1 и L2 заданы уравнениями с угловыми коэффициентами
y  k1x  b1 и y  k 2 x  b2
Рис. 5.
Найдем угол  , на который надо повернуть в положительном направлении прямую
L1 вокруг точки их пересечения до совпадения с прямой L2 .
Имеем  2    1 или    2  1 . Если    / 2 , то
tg  tg 2  1  
tg 2  tg1
1  tg1  tg 2
Но tg1  k1 , tg 2  k 2 , поэтому
tg 
k 2  k1
1  k1k 2
(3)
Формула (3) определяет один из углов между прямыми. Второй угол равен    .
Условие параллельности двух прямых.
Для того чтобы прямые
коэффициентами
y  k1 x  b1
и
L1
и
L2 , заданные уравнениями с угловыми
y  k 2 x  b2
соответственно,
были
параллельны,
необходимо и достаточно, чтобы
k1  k 2
(4)
131
Для того чтобы прямые L1 и L2 , заданные уравнениями A1 x  B1 y  C1  0 и
A2 x  B2 y  C2  0 соответственно, были параллельны, необходимо и достаточно, чтобы
A1 A2

B1 B2
или
A1 B1

A2 B2
(5)
Действительно, в этом случае условие параллельности можно записать так:
k1   A1 / B1  k 2   A2 / B2 .
Если
A1 B1 C1
A
B
, то прямые L1 и L2 совпадают. Если 1  1 , то прямые


A2 B2 C 2
A2 B2
пересекаются. Для нахождения координат их точки пересечения достаточно решить
систему двух уравнений с двумя неизвестными:
 A1 x  B1 y  C1

 A2 x  B2 y  C 2
Пусть

A1
B1
A2
B2
– определитель системы (6). Если
(6)
  0 , то прямые
пересекаются в одной точке и система (6) имеет единственное решение, которое можно
найти по формулам Крамера:
x
где  x 
 C1
B1
 C2
B2
, y 
x
y
, y


A1
 C1
A2
 C2
(7)
.
Легко показать, что если   0 , то прямые или параллельны и тогда система (6) не
имеет решений, или прямые совпадают и тогда система (6) имеет бесконечно много
решений.
Условие перпендикулярности двух прямых.
Для того чтобы прямые
L1
и
L2 , заданные уравнениями с угловыми
коэффициентами y  k1 x  b1 и y  k 2 x  b2 соответственно, были перпендикулярны (т.е.
   / 2 ) необходимо и достаточно, чтобы (см. формулу (3)):
k1  k 2  1
(8)
Для того чтобы прямые L1 и L2 , заданные уравнениями A1 x  B1 y  C1  0 и
A2 x  B2 y  C2  0 соответственно, были перпендикулярны, необходимо и достаточно,
чтобы
A1  A2  B1  B2  0
(9)
132
Действительно, в этом случае условие перпендикулярности можно записать так:
A1 / B1  A2 / B2  1 или A1 A2 / B1 B2  1. Отсюда следует (9).
Уравнение прямой, проходящей через данную точку перпендикулярно данному
вектору.
Пусть прямая проходит через заданную точку M 0 ( x0 , y0 ) перпендикулярно
данному ненулевому вектору n( A, B) . Вектор n( A, B) , перпендикулярный прямой,
называется нормальным вектором этой прямой.
Выведем уравнение прямой. Угловой коэффициент нормального вектора n( A, B)
равен k1  B / A . Тогда угловой коэффициент прямой, перпендикулярной к нормальному
вектору равен
y
k 2  1 / k 2   A / B . Уравнение такой прямой запишем в виде
A
A
x  C . Так как точка M 0 ( x0 , y0 ) лежит на прямой, то получим y 0   x 0  C ,
B
B
откуда определим неизвестный коэффициент
C : C  y 0  Ax0 / B . Следовательно,
уравнение прямой имеет вид
A( x  x0 )  B( y  y0 )  0
(10)
133
СЕМИНАР 10.
Пример 1. Найти расстояние от точки B (5;1) до прямой 5 x  2 y  16  0 .
Решение. В силу формулы (2) ( d 
d
Ax0  By 0  C
A2  B 2
5  5  2  1  16
5 2  ( 2 ) 2
):
7

25  4
=
7
.
29
Пример 2. Найти расстояние от точки P ( 2;1) до прямой 4 x  3 y  10  0 .
Решение. В силу формулы (2):
4  2  3  1  10
d
4 2  32

15
16  9
3
Пример 3. Найти расстояние от точки M 0 (7;4) до прямой, заданной уравнением
4 x  3 y  15  0 .
Решение. В силу формулы (2) d 
4   7   3  4  15
4 2  32

 55
16  9
 11
Пример 4. Найти расстояние от точки M 0 (2;1) до прямой 3x  4 y  22  0 .
Решение. В силу формулы (2):
d
3  2  4  1  22
32  4 2

 20
9  16
4
Пример 5. Найти расстояние от точки M 0 (2;1) до прямой  3x  4 y  15  0 .
Решение. По формуле получаем d 
 3  2  4  (1)  15
(3) 2  4 2

5
 1.
5
Пример 6. Составить уравнение прямой, проходящей через точку M  2;5 параллельно
прямой 3x  4 y  2  0 .
Решение. Разрешив последнее уравнение относительно y, получим y  (3 / 4) x  1 / 2 .
Следовательно, в силу условия параллельности угловой коэффициент искомой прямой
равен
-3/4.
Воспользовавшись
уравнением
y  y1  k ( x  x1 ) ,
получаем
y  (5)  (3 / 4)[ x  (2)] , т.е. 3x  4 y  26  0 .
Пример 7. Составим уравнение прямой, проходящей через точку M 1;1 перпендикулярно
прямой 2 x  3 y  1  0 .
Решение. Находим угловой коэффициент заданной прямой: k1 = −2/3. Так как искомая
прямая перпендикулярна данной, то ее угловой коэффициент k 2  1/ k1  3 / 2 . Уравнение
134
прямой с k = 3/2 имеет вид: y = 3x/2 + b. Подставляя в уравнение y = 3x/2 + b координаты
точки M (x = 1 и y = 1), получаем уравнение относительно b : 1 = 3/2 + b. Отсюда b = −1/2 и
искомое уравнение прямой y = 3x/2 − 1/2. Ответ: уравнение прямой 3x  2 y  1  0 .
Пример 8. Выяснить взаимное расположение двух прямых L1 : 3x  4 y  11  0 и
L2 : 2 x  3 y  8  0 и если они пересекаются, найти их точку пересечения.
Решение.

Решим
систему
3 4
 9  8  1  0 ,
2 3
следовательно,
координаты точки пересечения:  x 
y
3x  4 y  11
.

 2 x  3 y  8
прямые
Определитель
системы
пересекаются.
Вычисляем
 11  4
3  11

 1,  y 
 2 , x  x  1 ,
8 3
2 8

y
 2 . Прямые пересекаются в точке  1;2 .

Пример 9. Пересекаются ли прямые 3x  4 y  1  0 и 2 x  3 y  1  0 ?
1 4y

x

3x  4 y  1  0 
 x  1
3
Решение: Решим систему уравнений: 
,
,
.
2 x  3 y  1  0 2  1  4 y  3 y  1  0  y  1
3

Система имеет единственное решение, следовательно, прямые пересекаются. Точка
пересечения прямых имеет координаты (-1;1).
Пример 10. Выяснить взаимное расположение прямых 2 x  y  2  0 и 4 x  2 y  1  0 .
 2x  y  2  0
Решение: Решим систему уравнений 
. Эта система не имеет решений,
4 x  2 y  1  0
следовательно, прямые параллельны.
Пример 11. Выяснить взаимное расположение прямых x  y  1  0 и 3 x  3 y  3  0 .
Решение: Совпадают, так как коэффициенты пропорциональны.
Пример 12. Составить уравнение прямой линии, проходящей через точку пересечения
прямых x  y  1  0 , x  y  2  0 и через точку (2,1).
Решение: Находим координаты точки пересечения двух данных прямых линий. Для этого
решаем данные уравнения совместно. Складывая, находим: 2x  1  0 , откуда x  1/ 2 .
Вычитая из первого уравнения второе, получаем: 2 y  3  0 , откуда y  3 / 2 . Далее,
135
 1 3
остается составить уравнение прямой линии по двум точками   ;  и (2;1). Искомое
 2 2
3
1
3
1
y
x
x
2 
2 , или
2 
2 ,откуда x  5 y  7  0 .
уравнение будет:
3
1
1
5
1
2
2
2
y
Пример 13. Найти угол между прямыми y  2 x  1 и y  0,5 x  3 .
Решение. По формуле получим tg  (k 2  k1 ) (1  k1 k 2 )  (2  0,5 ) (1  2  0,5) 
3
, где
4
k1  2 , k2  0,5 ,   arctg 3 4 . Здесь угол отсчитывается от прямой y  2 x  1 .
Пример 14. Найти тангенс угла между диагоналями BD и AC , если заданы координаты
точек A( 2;3) , C (3;4) и уравнение диагонали BD y 
9
x 8.
5
Решение. Найдем уравнение диагонали AC как уравнение прямой, проходящей через две
данные точки:
x2
y3

. Следовательно, общее уравнение диагонали AC имеет вид
32  43
x  y  1  0 , уравнение с угловым коэффициентом – вид y   x  1 , угловой коэффициент
9
k1 прямой AC равен  1 . Угловой коэффициент диагонали BD равен k 2  . Тангенс
5
угла  между прямыми y  k1x  b1 и y  k 2 x  b2 определяется формулой tg 
k 2  k1
.
1  k1k 2
9
14
 (1)
7
7
Следовательно, tg  5
 5  . Отсюда   arctg .
9
4
2
2
1   (1)

5
5
Пример 15. Найти угол между прямыми, заданными уравнениями 5 x  3 y  15  0 и
x  4y  7  0 .
Решение.
Преобразуем
k k
tg  2 1 =
1  k1k 2
уравнения
к
виду:
5
y   x  5,
3
1
7
y  x ,
4
4
1 5

4 3  1. Следовательно,   450 .
5 1
1 
3 4

Пример 16. Составить уравнение прямой линии, проходящей через точку M 4;5 и
параллельной прямой 3x  4 y  12  0 .
136
Решение. Для того чтобы прямые L1 и L2 , заданные уравнениями A1 x  B1 y  C1  0 и
A2 x  B2 y  C2  0 были параллельны, необходимо и достаточно, чтобы
A1 B1
.

A2 B2
Поэтому искомое уравнение имеет вид 3x  4 y  C  0 , где C пока не определено.
Подставляя координаты x  4 и y  5 в уравнение 3x  4 y  C  0 , получаем, что C  8 .
Таким образом, уравнение прямой имеет вид 3x  4 y  8  0 .
Пример 17. Составить уравнение прямой линии, проходящей через точку M  3;2 и
перпендикулярной прямой 4 x  5 y  7  0 .
Решение. Для того чтобы прямые L1 и L2 , заданные уравнениями A1 x  B1 y  C1  0 и
A2 x  B2 y  C2  0
были
перпендикулярны,
необходимо
и
достаточно,
чтобы
k 2   A2 / B2  1 / k1  B1 / A1 . Поэтому искомое уравнение имеет вид 5 x  4 y  C  0 , где
C пока не определено. Подставив в это уравнение координаты точки M x0  3 и y  2 ,
получаем  15  8  C  0 или C  23 . Таким образом, уравнение прямой имеет вид
5 x  4 y  23  0 .
Пример 18. Найти расстояние от точки пересечения прямых l1 и l 2 до прямой l 3 .
Определить взаимное расположение пар прямых l1 , l 3 и l 2 , l 3 , если прямые заданы
общими уравнениями: l1 : 3 x  2 y  1  0,
l 2 : x  y  3  0,
3х  2 у  1  0;
Решение. Решим систему уравнений: 
 х  у  3  0.
l3 :  6 x  4 y  3  0.
Получим: x0  1 , y 0  2 –
единственное решение. Следовательно, прямые l1 и l 2 пересекается в точке M 0 1;2 .
Найдем расстояние d от M 0 1;2 до l3 : d 
 6 1  4  2  3
36  16

1
52
. Нормальные векторы
прямых l1 , l 2 и l3 соответственно будут n1 3;2 , n2 1;1 , n3  6;4 . Так как координаты n1
и n3 пропорциональны 3/(–6)=–2/4, то l1  l3 . Для l 2 и l3 имеем: 1/(–6)  1/4,
следовательно, l 2 и l3 пересекаются.
137
ЛЕКЦИЯ 11. Линии второго порядка.
В качестве примера найдем уравнения задающие окружность, параболу, эллипс и
гиперболу.
Окружность.
Окружностью называется множество точек плоскости, равноудалённых от
заданной точки, называемой центром, на заданное ненулевое расстояние R , называемое
её радиусом (рис. 1).
Рис. 1. Окружность.
Пусть точка C (центр) имеет координаты  ;   . Расстояние от точек окружности
M x; y  до центра обозначим через R . Тогда будем иметь:
MC 
x   2   y  b2
 x    2   y   2
 R или
 R2
(1)
Полагая в (1)   0 и   0 , получаем уравнение окружности радиусом R с
центром в начале координат:
x2  y2  R2
(2)
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма
расстояний от двух заданных точек F1 , F2 , называемых фокусами эллипса, есть
величина постоянная, большая, чем расстояние между фокусами.
138
Выведем уравнение эллипса на координатной плоскости. Пусть F1 , F2 - фокусы
эллипса. Длину отрезка F1 F2 обозначим через 2c , сумму расстояний от произвольной
точки эллипса Ax; y  до фокусов 2a  AF1  AF2 ( 2a  2c или a  c ). Числа AF1 и AF2
называются фокальными радиусами точки Ax; y  .
Введем систему координат, считая началом координат O середину отрезка F1 F2 ,
осью абсцисс - прямую F1 F2 , осью ординат - прямую, проходящую через начало
координат и перпендикулярную оси абсцисс (рис. 2). Фокусы эллипса будут иметь
координаты F1  c;0 , F2 c;0 .
Рис. 2. Эллипс.
Расстояния
соответственно
от
произвольной
x  c2  y 2
и
точки
эллипса
x  c2  y 2 .
Ax; y 
до
фокусов
равны
Точка Ax; y  принадлежит эллипсу в
том и только том случае, когда выполняется равенство
x  c2  y 2  x  c2  y 2
 2a ,
т.к. по определению эллипса AF1  AF2  2a .
Перенесем второе слагаемое левой части этого равенства в правую часть и
возведем обе части полученного равенства в квадрат. Будем иметь
Приведем подобные члены
a
x  c2  y 2
 a 2  xc
Еще раз возведем в квадрат и приведем подобные члены


x 2 a 2  c 2  y 2a 2  a 4  a 2c 2
139
Обозначим
и разделим обе части равенства на
Получим
равенство
x2 y2

1
a2 b2
(3)
которое называется каноническим уравнением эллипса. Эллипс – линия второго порядка.
Рис. 3. Малая и большая полуоси эллипса.
График эллипса симметричен относительно осей Ox и Oy , т.к. уравнение (3)
содержит члены только с четными степенями x и y . При x  0 : y  b . При y  0 :
x   a (рис. 3). Если a  b , то уравнение (3) принимает вид x 2  y 2  a 2 . Это уравнение
окружности с радиусом a .
Оси симметрии эллипса называются его осями. А точка пересечения осей –
центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами.
Т.к. b  a 2  c 2 , то a  b . Величины a и b называются соответственно большой и
малой полуосями. Ответственно оси эллипса называются большой и малой.
Эксцентриситетом эллипса называется отношение   c / a . Т.к. c  a , то
c2 a2  b2
b
b
 1    . Следовательно,  1   2 .
0    1 . Т.к. c  a  b , то   2 
2
a
a
a
a
2
2
2
2
2
Отсюда следует геометрическое истолкование эксцентриситета. При очень малом 
эллипс близок к окружности. Если  близок к единице b  a эллипс сильно вытянут
вдоль большой оси. Таким образом,  - мера вытянутости эллипса.
Планеты вращаются по эллиптическим траекториям с малыми  , а кометы с
большими  .
140
Гипербола
Гиперболой
называется
геометрическое
место
точек
плоскости,
разность
расстояний от которых до двух заданных точек F1 , F2 , называемых фокусами
гиперболы, есть величина постоянная, взятое со знаком "+" или "–" и меньшее, чем
расстояние между фокусами.
Выведем уравнение гиперболы. Введем систему координат, считая осью Ox
прямую, проходящую через фокусы, а осью Oy прямую, перпендикулярную оси Ox , и
делящую отрезок F1 F2 пополам. Пусть фокусы имеют координаты F1  c;0 , F2 c;0
(рис. 4).
Рис. 4. Гипербола.
Обозначим через 2a модуль разности расстояний от произвольной точки Ax; y 
гиперболы до фокусов. Причем 0  a  c . По определению гиперболы точка Ax; y 
принадлежит гиперболе тогда и только тогда, когда выполняется равенство
AF1  AF2  2a . Числа AF1 , AF2 называются фокальными радиусами точки Ax; y  .
Причем
AF1  r1 
x  c2  y 2 ,
AF2  r2 
x  c2  y 2
(4)
Перепишем равенство AF1  AF2  2a в координатной форме с учетом (4)
x  c2  y 2
-
x  c2  y 2 =  2a .
(5)
Перенесем второй корень в правую часть и возведем обе части равенства в квадрат.
Получим
Раскрывая скобки и приводя подобные члены, будем иметь равенство
141
(6)
Еще раз, возводя в квадрат и обозначая b  c 2  a 2 (при этом c  a ), получим
.
Разделив обе части на
, окончательно получим уравнение гиперболы
(7)
Уравнение (7) называется каноническим уравнением гиперболы. Так как (7) содержит
члены только с четными степенями x и y , то гипербола симметрична относительно осей
координат и начала координат.
Рис. 5. Оси гиперболы.
Гипербола состоит из двух ветвей (правой и левой) и имеет две асимптоты:
y
b
x,
a
y
b
x.
a
(8)
Ось Ox и Oy являющиеся осями симметрии, называются осями гиперболы, а центр
симметрии (точка пересечения осей) – центром гиперболы.
Одна из осей пересекается с гиперболой в двух точках с координатами  a;0 и
a;0 ,
которые называются ее вершинами. Эта ось называется действительной осью
гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью
гиперболы. Прямоугольник со сторонами 2a и 2b (рис. 5) называются основным
прямоугольником
гиперболы.
Величины
a
и
b
называются
соответственно
действительной и мнимой полуосями гиперболы.
Гипербола с равными полуосями
a  b
называется равносторонней и ее
каноническое уравнение имеет вид:
142
x2  y2  a2
Эксцентриситетом гиперболы называется отношение   c / a , где c - половина
расстояния между фокусами, a - действительная полуось гиперболы. Так как c  a , то
  1 . Заметив, что c 2  a 2  b 2 , найдем
c2 a2  b2
b
b
  2 
 1      2 1
2
a
a
a
a
2
2
(9)
Следовательно, чем ближе  к единице, т.е. чем  меньше, тем меньше b / a , а это
означает, что основной прямоугольник более вытянут в направлении действительной оси.
Из (6), (4), (5) и (9) получаем
 ar1  ar2  2a 2  xc  a 2
 ar2  xc  a 2 ,
Отсюда следует, что фокальные радиусы правой ветви гиперболы вычисляются по
формулам
r2  x  a
r1  x  a ,
(10)
Фокальные радиусы точки левой ветви - по формулам
r1  x  a ,
r2  x  a
(11)
Напомним, что для эллипса: c  a  b , для гиперболы: c  a  b .
2
2
2
2
2
2
Директрисы эллипса и гиперболы.
Определение.
Две
прямые,
перпендикулярные
большой
расположенные симметрично относительно центра на расстоянии
оси
a/
эллипса
и
от него,
называются директрисами эллипса. Их уравнения:
x
a

;
x
a

(12)
Т.к. для эллипса   1, то a /   a (рис. 6).
Рис. 6. Директрисы параболы
143
Определение. Две прямые, перпендикулярные действительной оси гиперболы и
расположенные симметрично относительно центра на расстоянии
a/
от него,
называются директрисами гиперболы. Их уравнения:
x
a

x
;
a
(13)

Т.к. для гиперболы   1 , то a /   a (рис. 5).
Парабола.
Параболой называется геометрическое место точек, равноудаленных от данной
прямой d , называемой директрисой, и данной точки F , называемой фокусом параболы
и не проходящей через фокус.
Выведем уравнение, задающее параболу на координатной плоскости.
Рис. 7. Парабола.
Введем систему координат, считая началом координат O середину отрезка длиной
p
между полюсом параболы и директрисой (рис. 7). Величину
p
называют
параметром параболы, а ось ординат - осью параболы. Тогда фокус F будет иметь
координаты F  p / 2;0 .
Пусть M x; y  - произвольная точка плоскости. Расстояния от нее до фокуса и
директрисы равны соответственно
p
p

MF   x    y 2 и MK  x 
2
2

(14)
Точка M x; y  принадлежит параболе в том и только том случае (по определению
параболы), когда выполняется равенство
144
p
p

MF   x    y 2  x 
2
2

Возведя обе части этого равенства в квадрат и приведя подобные члены, будем
иметь равенство
y 2  2 px ,
(15)
которое и будет искомым уравнением параболы. Уравнение (15) называется
каноническим уравнением параболы.
Фокальный радиус её точки M x; y  вычисляется по формуле
p
p

MF   x    y 2  x 
2
2

(16)
Парабола является линией второго порядка. Т.к. (15) содержит y только в четной
степени, то парабола симметрична относительно оси Ox .
Возьмем точку с координатой x  1. Соответствующие две точки на параболе




имеют координаты: M 1 1; 2 p и M 2 1; 2 p . Расстояние между ними равно 2 2 p .
Это расстояние тем больше, чем больше p . Следовательно, параметр p характеризует
«ширину» области, ограниченной параболой.
Уравнение директрисы параболы имеет вид:
x
p
2
(17)
Парабола, симметричная относительно оси Oy и проходящая через начало
координат, определяется уравнением
x 2  2qy
(18)
Фокус этой параболы находится в точке F 0; q / 2 , уравнение директрисы имеет
вид y   q / 2 . Фокальный радиус ее точки M x; y  выражается формулой
MF  y 
q
2
(19)
145
СЕМИНАР 11.
Пример 1. Покажите на координатной плоскости множество точек, которое задается
неравенством x 2  y 2 9
Решение. Множество точек плоскости, удовлетворяющих данному неравенству, выделено
на рисунке серым цветом.
Пример
2.
Даны
x  12   y  32
точки
A0;0 ,
B 2;1 ,
C3;3
D2;1
и
и
окружность
 25 . Выясните, где расположены эти точки: на окружности, внутри или
вне окружности?
Решение. Подставив координаты данных точек в левую часть уравнения данной
окружности, найдём квадраты расстояний от данных точек до центра O1;3 окружности:
OA 2  0  1  0  3  10  25
2
2
OB 2   2  1  1  3  25  25
2
2
OC 2  3  1  3  3  40  25
2
2
OD 2  2  1   1  3  5  25
2
2
Следовательно, точки A и D расположены внутри окружности, точка B — на
окружности, а точка C — вне окружности.
Пример
3.
Найти
координаты
центра
окружности
C,
заданной
уравнением
x 2  y 2  6x  4 y  7  0 .
Решение. x 2  y 2  6 x  4 y  7  x 2  6 x  9  y 2  4 y  4  7  9  4  x  3   y  2  6 .
2
2
Следовательно, координаты центра окружности C3;2 .
Пример 4. Найти координаты центра C и радиус окружности, определяемой уравнением
4 x 2  4 y 2  8 x  12 y  3  0 .
146
Решение. Разделив обе части уравнения на 4 и выделив полные квадраты, получим
2
3
9
9 3
3

2
x  2 x  1  y  2  y   1    0   x  1   y    4
2
4
4 4
2

2
2
Сравнивая полученное уравнение с уравнением (5.15), заключаем, что   1 ,
  3 / 2 , R  2 .
Пример
5.
Какое
множество
точек
плоскости
определяет
уравнение
x 2  y 2  4 x  10 y  29  0 ?
Решение. Так как это уравнение сводится к уравнению x  2    y  5  0 , которому
2
2
удовлетворяют лишь координаты x  2 , y  5 , то оно определяет единственную точку
C 2;5 .
Пример 6. Найти координаты центра окружности 2 x 2  2 y 2  8 x  5 y  4  0 .
Решение. Для того, что бы множитель при x2 и y2 были равны единице, делим обе части
равенства на 2 и перегруппировываем члены выражения
x
2

5 

 4  x   y 2  y   2.
2 

Достроим выражения в фигурных и квадратных скобках до полных квадратов, прибавив к
2
5
фигурным скобкам 4, а квадратным   (одновременно прибавляя те же величины и
4
справа):
2
2
5
25 
25
5
121  11 


( x  4  x  4)   y 2   y    2  4  , или ( x  2) 2   y   
  .
2
16 
16
4
16  4 


2
5

Ответ. Исходное уравнение определяет окружность с центром в точке  2;   и
4

радиусом
11
.
4
Пример 7. Найти координаты центра и радиус окружности, если ее уравнение задано в
виде: 2 x 2  2 y 2  8 x  5 y  4  0 .
Решение. Для нахождения координат центра и радиуса окружности данное уравнение
необходимо привести к виду
 x    2   y   2
 R 2 . Для этого выделим полные
квадраты. Разделим левую и правую часть на 2:
147
x 2  y 2  4 x  2.5 y  2  0
x 2  4 x  4  4  y 2  2.5 y 
 x  2
25 25

20
16 16
2
2
5  25

y  
6  0
4  16

2
5
121
 x  2    y   
4
16

5
11

O  2,   ; R 
4
4

2
Пример 8. Найти координаты точки O1 , которая равноудалена от трех точек A7;1 ,
B 2;2 и C 1;5 (см. рисунок).
Решение. Из формулировки условия задачи следует, что O1 A  O1 B  O1C Пусть искомая
точка O1 имеет координаты a; b . По формуле d 
O1 A 
x A  xB 2   y A  y B 2
a  72  b  12 ; O1 B  a  22  b  22
; O1C 
 a  7 2  b  12 
Составим систему из двух уравнений: 
2
2
 a  7   b  1 
найдем:
a  12  b  52
a  22  b  22 .
a  12  b  52
После возведения в квадрат левой и правой частей уравнений запишем:
a  7 2  b  12  a  22  b  22

2
2
2
2
 a  7   b  1  a  1  b  5
 3a  b  7  0
Упростив, запишем: 
. Решив систему, получим: a  2 , b  1 .
 2a  b  3  0
Точка O1 2;1 равноудалена от трех заданных в условии точек, которые не лежат
на одной прямой. Эта точка – есть центр окружности, проходящей через три заданные
точки (см. рисунок).
148
Пример 9. На рисунке изображено некоторое множество точек. Из двух неравенств
выберете то, которому оно соответствует:
x2 y 2
x2 y 2

1 и

 1.
25 9
25 9
Решение. Множество точек изображенных на рисунке, соответствует неравенству
x2 y 2

 1.
25 9
Пример 10. Какую линию определяет уравнение 3x 2  4 y 2  12 ?
Решение. Разделим это уравнение почленно на 12:
x 2 / 4  y 2 / 3  1 . Сравнивая
полученное уравнение с уравнением (5.17), заключаем, что оно определяет эллипс с
полуосями a  2 , b  3 . Найдем фокусы этого эллипса. Из формулы c 2  a 2  b 2
следует, что c 2  4  3  1 , c  1 . Следовательно, фокусы эллипса находятся в точках
F1  1;0 , F2 1;0 .
Пример 11. В прямоугольной декартовой системе координат построить линию,
определяемую уравнением y  
2
9  x2 .
3
Решение. Преобразуем это уравнение, возведя в квадрат обе его части:
y2 
y2 9  x2 x2 y2
4
9  x2 ,

,

1
9
4
9
9
4


Последнее уравнение определяет эллипс с полуосями a  3 , b  2 . Если решить это
уравнение относительно y , получим y 
2
2
9  x2 , y  
9  x2 .
3
3
В условии задачи дано второе из этих уравнений. Оно определяет не весь эллипс, а
только ту его часть, для точек которой y  0 , т.е. половину эллипса, расположенную
ниже оси Ox .
149
Пример 12. Записать каноническое уравнение эллипса, проходящего через точки M 3;2 ,


N 3 3 / 2, 2 .
Решение. Каноническое уравнение эллипса имеет вид x 2 / a 2  y 2 / b 2  1. Так как точки
M и N лежат на эллипсе, то их координаты удовлетворяют уравнению эллипса:
32 2 2

 1,
a2 b2
3
3/ 2
a2
   2
2
2
b
2
 1,
систему уравнений, находим, что
9
4
 2  1,
2
a
b
a 2  18 ,
27
2
 2  1 . Решая полученную
2
2a
b
b2  8 .
Таким образом, получено
каноническое уравнение эллипса x 2 / 18  y 2 / 8  1 .
Пример 13. Получить каноническое уравнение эллипса, проходящего через точки
5
6 
M  ;
 и
2 4 

15 
N   2 ;
.
5 

Решение. В данном случае «получить каноническое уравнение эллипса» - значит, найти
конкретные значения a и b (большой и малой полуосей). Отметим то, что точек у нас две и
неизвестных тоже две, т.е. может быть получена система алгебраических уравнений:
подставляем координаты первой точки в одно уравнение эллипса, а второй точки – во
второе
 25
 4  a 2
 4
 2
 a
3
8  b2
3
5  b2


 1
 решая систему любым способом  a 2  10 ; b 2  1.
 1
x2 y2

 1.
Т.о., искомое каноническое уравнение эллипса
10 1
Пример 14. Составить уравнение эллипса, если его фокусы: F1 0;0 , F2 1;1 , большая ось
равна 2.
Решение. Уравнение эллипса имеет вид:
2c  (1  0) 2  (1  0) 2  2 , c 
x2 y2

 1 . Расстояние между фокусами:
a2 b2
2
, по условию 2a  2 , следовательно a  1 .
2
1
1
2
x2
y2
2
 1.
Таким образом, c  a  b   1  b  b  1  
. Итого: 2 
2
2
2
1/ 2
1
2
2
2
Пример 15. Какую линию определяет уравнение 9 x 2  4 y 2  36 ?
Решение. Разделив обе части уравнения на 36, получим x 2 / 4  y 2 / 9  1 . Сравнивая это
уравнение с уравнением (7), заключаем, что оно определяет гиперболу с действительной
полуосью a  2 и мнимой полуосью b  3 .
150
Пример 16. Найти полуоси, координаты фокусов и эксцентриситет гиперболы, заданной


уравнением 5 x 2  4 y 2  20 . Вычислить длины фокальных радиусов точки M  4; 15 .
Решение. Разделив обе части уравнения на 20, получим x 2 / 4  y 2 / 5  1 . Сравнивая это
уравнение с уравнением (5.21), заключаем, что a 2  4 , b 2  5 , т.е. a  2 , b  5 .
Так как c 2  a 2  b 2 , c  3 , F1  3;0 , F2 3;0 . По формуле (9) находим   c / a  3 / 2.
Поскольку точка M
фокальных
радиусов
лежит на левой ветви гиперболы, то при вычислении длин
и
r1
r2
необходимо
пользоваться
формулами
(11):
r1   3 / 2 4  2  4 , r2   3 / 2 4  2  8 .
 x 2  y 2  25
Пример 17. Решить графически систему уравнений 
.
 xy  12
Решение. Графиком уравнения x 2  y 2  25 является окружность с центром в начале
координат и радиусом, равным 5 (см. рисунок). Графиком уравнения xy  12 является
гипербола y  12 / x (красная кривая на рисунке). Построив графики в одной системе
координат, найдём координаты точек A , B , C , D пересечения окружности и гиперболы:
A4;3 , B3;4 , C  4;3 , D 3;4 . Значит, решения заданной системы таковы: 4;3 ,
3;4 ,  4;3 ,  3;4 .
Пример 18. Записать уравнение асимптот и директрис гиперболы 4 x 2  9 y 2  36 .
Решение. Приведя уравнение гиперболы к каноническому виду (5.21), заключаем, что
a 2  9 , b 2  4 , т.е. a  3 , b  2 . В соответствии с (5.22) записываем уравнения асимптот
y  2 / 3x ,
y  2 / 3x .
эксцентриситет
С
учетом
c2  a2  b2
находим
c  9  4  13 ,
а
  c / a  13 / 3 . Согласно (5.27), получаем уравнения директрис
x  9 / 13 ; x  9 / 13
151
Пример 19. Найти координаты вершины параболы, заданной уравнением x  y 2  4 y  1 .
Написать уравнение оси симметрии.
Решение:
Найдем
координаты
вершины
параболы:
x  y2  4 y  4  4 1 ,
x   y  2   3 , x  3   y  2  . Следовательно, вершина параболы лежит в точке
2
2
 3, 2 . Уравнение оси параболы
y  2 .
Пример 20. Найти координаты фокуса и уравнение директрисы параболы y 2  8 x .
Вычислить расстояние точки M 2;4 до фокуса.
Решение. Сравнивая уравнение y 2  8 x с каноническим уравнением параболы, находим,
что 2 p  8 , откуда p  4 , p / 2  2 . В соответствие с формулой получаем уравнение
x  2 директрисы параболы, фокус параболы находится в точке F 2;0 . Точка M 2;4
лежит на параболе, так как ее координаты удовлетворяют уравнению y 2  8 x . По
формуле (5.33) находим фокальный радиус точки M : r  2  2  4 .
Пример 21. Найти координаты фокуса и уравнение директрисы параболы x 2  4 y .
Вычислить расстояние точки M 6;9 до фокуса.
Решение. Сравнивая уравнение x 2  4 y с каноническим уравнением параболы, находим,
что 2q  4 , откуда q  2 , q / 2  1 . Следовательно, согласно (5.33) фокус параболы
находится в точке M : r  9  1  10 .
Пример 22. Составить уравнение параболы, симметричной относительно оси Ox и
проходящей через точки M 5;4 , N 15;6 .
Решение. Так как парабола симметрична относительно оси Ox , то в её уравнение y
входит только во второй степени. Уравнение этой параболы имеет вид y 2  2 px  c , где
p и c - некоторые постоянные. Найдем p и c , использовав условия задачи. Поскольку
точки M и N лежат на параболе, то их координаты должны удовлетворять её уравнению
4 2  2 p  5  c ,  6   2 p  15  c . Из уравнений 16  10 p  c , 36  30 p  c находим p  1 ,
2
c  6 . Таким образом, данная парабола определяется уравнением y 2  2 x  6 .
Пример 23. Эксцентриситет гиперболы равен
2 . Найти каноническое уравнение
гиперболы, если точка М ( 3 ; 2 ) принадлежит гиперболе.
Решение. Необходимо найти значения a и b в каноническом уравнении гиперболы.
Неизвестных величин две, следовательно, и уравнений для их нахождения должно быть
два.
152
Первое уравнение получим из того факта, что нам известен эксцентриситет
гиперболы и известна связь между полуосями и координатами фокуса гиперболы:
с
2
2
2
2
2
a  a  b  2a  a  b .
 a 2  b2


c2
Это первое равенство, а второе получим, используя тот факт, что точка М
гиперболе принадлежит, т.е., ее координаты обращают каноническое уравнение
гиперболы в тождество:
x2 y2
( 3) 2 ( 2 ) 2
3
2


1


 1  2  2  1,
2
2
2
2
a
b
a
b
a
b
2
2
но a  b (наше первое равенство), тогда a  b  1
и, окончательно, получаем,
что
искомая
гипербола описывается каноническим
уравнением x2 - y2 = 1.
Пример 24. Составить каноническое уравнение эллипса, зная, что большая его ось 2a  10
и эксцентриситет   0.8 .

Решение. По формуле
c
,
a
c  a  5  0.8  4 , а b
a 2  b2  c 2 , b2  a 2  c 2 , b2  25  16  9, b  3 .Подставляя
a  5, b  3 в уравнение
находим из равенства
найденные
значения
x2 y2
x2 y2
,
получим
искомое
уравнение
эллипса


1

 1.
25 9
a2 b2
Пример 25. Написать уравнение гиперболы по данной полуоси a  1 и полуфокусному
расстоянию c  2 .
Решение. Из a 2  b 2  c 2 , b 2  c 2  a 2 , b 2  4  1, b  3 . Искомое уравнение гиперболы
2
2
будет иметь вид х  у 1
1 3
Пример 26. Найти координаты фокуса и уравнение директрисы параболы x  5 y 2 .
Решение. Перепишем уравнение так: y 2  
1
5
получим 2 p   , p 
x
x
2
и, сравнивая его с уравнением y  2 px ,
5
1
 1 
. Координаты фокуса   , 0  и уравнение директрисы
10
 20 
1
.
20
Пример 27. Найти координаты вершины параболы, заданной уравнением x  y 2  4 y  1 .
Написать уравнение оси симметрии.
153
Решение.
Найдем
координаты
вершины
x  y2  4 y  4  4 1 ,
параболы:
x   y  2   3 , x  3   y  2  . Следовательно, вершина параболы лежит в точке
2
2
 3, 2 . Уравнение оси параболы
y  2 .
Пример 28. Привести уравнение кривой второго порядка 4 x 2  y 2  16 x  2 y  8  0 к
каноническому виду и построить кривую.
Решение. Для приведения уравнения кривой второго порядка к каноническому виду
применяют метод выделения полного квадрата. Сгруппируем слагаемые, содержащие
текущие
координаты.
Коэффициенты
4( x 2  4 x)  ( y 2  2 y)  8  0 .
при
x2
и
y2
Выделим
вынесем
за
полный
скобки:
квадрат:
4( x 2  4 x  4)  ( y 2  2 y  1)  8  16  1  0 . Отсюда 4( x  2) 2  ( y  1) 2  25 . Разделим обе
части равенства на 25:
каноническом виде:
4( x  2) 2 ( y  1) 2

 1 . Запишем полученное уравнение в
25
25
( x  2) 2 ( y  1) 2

 1 . Выполним параллельный перенос осей
25
25
4
 X  x  x0
координат по формулам 
. При таком преобразовании начало координат
Y  y  y 0
переносится в точку
( x0 , y0 ) , уравнение эллипса принимает канонический вид
X2 Y2
5
 2  1 . В нашем примере x0  2 , y 0  1, a  , b  5 . Итак, рассматриваемое
2
2
a
b
уравнение определяет эллипс с центром в точке С (2;1) и полуосями
5
и 5 (см. рисунок).
2
y
6
1
х
-4,5
0,5
-2
-4
Пример 29. Привести уравнение кривой второго порядка 4 x 2  16 x  2 y  1  0
к
каноническому виду и построить кривую.
Решение. Как и в предыдущем примере, сгруппируем слагаемые, содержащие текущие
координаты:
4( x 2  4 x)  2 y  1  0 .
В
скобках
выделим
полный
квадрат:
154
4( x 2  4 x  4)  16  2 y  1  0 ; 4( x  2) 2  2 y  15 . Отсюда ( x  2) 2 
1
15
( y  ) . Выполним
2
2
 X  x  2
15 . После этого преобразования уравнение параболы
замену переменных 
Y

y


2
принимает канонический вид X 2 
расположена в точке C (2;
1
Y , вершина параболы в системе координат Oxy
2
15
) (см. рисунок).
2
y
х
-2

15
2
Рис. 14
155
ЛЕКЦИЯ 12. Поверхности в пространстве и их уравнения.
Поверхность
Поверхность, определенная некоторым уравнением в данной системе координат,
есть геометрическое место точек, координаты которых удовлетворяют данному
уравнению
F x; y; z   0
(1)
Например, сферой называется геометрическое место точек, равноудалённых от
заданной т. C x0 ; y 0 ; z 0  являющейся центром сферы. Выведем уравнение сферы с
центром в точке C x0 ; y 0 ; z 0  и радиусом R . Обозначим как M x; y; z  точку с текущими
координатами
CM  R 
на
сфере.
В
x  x0 2   y  y0 2  z  z 0 2
этом
случае
(рис.
1)
 R.
Рис. 1.
Нормальное уравнение сферы находим посредством возведения обеих частей
равенства в квадрат:
x  x0 2   y  y0 2  z  z0 2  R 2
(2)
Общее уравнение плоскости
Известно, что любые не совпадающие и не лежащие на одной прямой три точки
определяют плоскость, причем единственную. Кроме того вектор нормали к плоскости
ориентирует ее в пространстве (рис. 2). Выведем уравнение такой плоскости.
156
Рис. 2.
Пусть искомая плоскость  проходит через точку M 0 x0 ; y 0 ; z 0  перпендикулярно

вектору n ( A; B; C ) и точка M x; y; z  - произвольная точка на плоскости  . Точка M  

 когда векторы M 0 M и n ( A; B; C ) взаимно перпендикулярны. Так как координаты



вектора M 0 M равны x  x0 , y  y 0 , z  z 0 (т.е. M 0 M  ( x  x0 )  i  ( y  y0 )  j  ( z  z 0 )k , ),
то в силу перпендикулярности векторов скалярное произведение M 0 M на вектор

n ( A; B; C ) равно нулю:
M M  n  Ax  x   B y  y   Cz  z   0
0
0
0
0
Раскрывая скобки, получаем
Ax  By  Cz   Ax0  By 0  Cz0   0
Обозначая число
 Ax0  By 0  Cz0 
через
D , получаем общее уравнение
плоскости:
Ax  By  Cz  D  0 ,
где
(3)

– координаты нормали плоскости n ( A; B; C ) .
Неполные уравнения плоскости.
Пусть плоскость задана своим общим уравнением (3). Тогда
1) если D =0, то (3) определяет плоскость, проходящую через начало координат;
2) если A =0, то By  Cz  D  0 и имеем плоскость, параллельную оси Ox (т.к.

n( 0 ; B ; C )  Ox );
3) если B =0, то Ax  Cz  D  0 и имеем плоскость, параллельную оси Oy (т.к.

n( A; 0 ; C )  Oy );
157
4) если C =0, то Ax  By  D  0 и имеем плоскость, параллельную оси Oz (т.к.

n ( A; B ; 0 )  Oz );
5) A =0; B =0, то Cz  D  0 и имеем плоскость, параллельную плоскости Oxy;
6) A =0; C =0, то By  D  0 и имеем плоскость, параллельную плоскости Oxz;
7) B =0; C =0, то Ax  D  0 и имеем плоскость, параллельную плоскости Oyz;
8) A =0, B =0, D =0, то Cz  0 – это плоскость Oxy;
9) A =0, C =0, D =0, то By  0 – это плоскость Oxz;
10) B =0, C =0, D =0, то Ax  0 – это плоскость Oyz.
Точно так же, как было ранее с общим уравнением прямой на плоскости, из общего
уравнения можно получить и другие формы уравнения плоскости. Одна из этих форм
уравнение плоскости в отрезках.
Нормальное уравнение плоскости.
Положение плоскости  определяется заданием единичного вектора e , имеющего
направление перпендикуляра ОК, проведенного на плоскость из начала координат, и
длиной p этого перпендикуляра (рис. 4).
Рис. 3.
Если α, β, γ – это углы, образованные единичным вектором e с осями Ох, Оу, Oz
соответственно. Выведем уравнение плоскости  .
Так как e - единичный вектор, то
e  cos  ; cos  ; cos  
Пусть M x; y; z  - произвольная точка, принадлежащая  . Тогда проекция вектора
OM на нормаль к плоскости равна p , т.е.


p  e  OM  x cos   y cos   z cos  ,
Откуда получаем
x  cos   y  cos   z cos   p  0
(4)
Уравнение (4) называется нормальным уравнением плоскости.
158
Общее уравнение плоскости (3) можно привести к нормальному уравнению (4),
умножив обе части уравнения (3) на нормирующий множитель   
1
A  B2  C 2
2
,
учитывая, что знак нормирующего множителя противоположен знаку свободного члена D
общего уравнения плоскости.
Расстояние от точки до плоскости.
Если точка M 0 имеет координаты x 0 , y 0 , z 0 , а плоскость задана нормальным
уравнением (4), то расстояние d от точки M 0 до этой плоскости определяется по
формуле:
d  x0  cos   y0  cos   z 0 cos   p
(5)
Пусть Q - проекция точки M 0 на нормаль (рис. 3). Тогда KQ  OQ  OK . Но
OQ  прe OM 0 ,
OK  p .
Следовательно,
d  KQ  прe OM 0  OK .
Вектор
OM 0  x0 ; y 0 ; z 0  , а прe OM 0  e  OM 0  x0 cos   y0 cos   z 0 cos  . Получаем формулу
(5).
Можно определить формулу для d , когда плоскость задана общим уравнением (3).
Если учесть, что нормирующий множитель   
d
1
A  B2  C 2
2
, то получим
Ax0  By 0  Cz 0  D
(6)
A2  B 2  C 2
Уравнение плоскости в отрезках
Из общего уравнения плоскости
плоскости
выражение
a
в
отрезках
на
D
Ax  By  Cz  D  0
получается уравнение
A  x  B  y  C  z  D  0  A  x  B  y  C  z  D .
слева
и
справа,
вводим
Делим
обозначения
D
D
D
,b ,c
получаем:
A
B
C
x y z
  1
a b c
(7)
Последнее выражение получило название «уравнение плоскости в отрезках», где a,
b и с - величины отрезков, отсекаемых плоскостью на осях Ox, Oy и Oz соответственно
(рис. 4).
159
Рис. 4.
Уравнение плоскости, проходящей через заданную точку перпендикулярно данному
вектору.
Если в пространстве Oxyz плоскость  задана точкой M 0 ( x0 ; y0 ; z 0 ) и вектором
n  Ai  B j  C k , перпендикулярным этой плоскости (рис. 5), то уравнение плоскости
имеет вид
A( x  x0 )  B( y  y0 )  C ( z  z 0 )  0
(8)
Рис. 5.
Уравнение плоскости по трем точкам
Пусть M 1 ( x1 ; y1 ; z1 ) , M 2 ( x2 ; y2 ; z 2 ) , M 3 ( x3 ; y3 ; z 3 )   . Выберем произвольную
точку M ( x; y; z )   .
Рис. 6.
160
Тогда
M 1 M  x  x1 ; y  y1 ; z  z1 ,
M 1 M 2  x2  x1 ; y2  y1 ; z 2  z1  ,
M 1 M 3  x3  x1 ; y3  y1 ; z 3  z1  . Т.к. векторы лежат в одной плоскости, они компланарны,
следовательно, их смешанное произведение равно нулю: M 1 M  M 1 M 2  M 1 M 3 
(9)
– уравнение плоскости по трем точкам.
Угол между двумя плоскостями
Пусть две плоскости  1 и  2 заданы своими общими уравнениями
A1 x  B1 y  C1 z  D1  0
A2 x  B2 y  C2 z  D2  0
Т.е., векторы-нормали имеют координаты для плоскости  1  n1 ( A1 ; B1 ; C1 ) , для
плоскости  2  n2 ( A2 ; B2 ; C2 ).
И пусть плоскости не совпадают и не параллельны (рис. 7).
Рис. 7.
Угол между плоскостями определяется углом между нормальными векторами
 
n1 и n2 , а как найти угол между векторами мы уже знаем. Если  – угол между векторами
 
n1 и n2 , то это же и угол между плоскостями  1 и  2
 
n1  n2
A1  A2  B1  B2  C1  C 2
cos     
(10)
n1  n2
A12  B12  C12  A22  B22  C 22
Откуда получаем два важных следствия
Условие перпендикулярности двух плоскостей
Из формулы (10) следует, что две плоскости перпендикулярны при условии:
161
A1 A2  B1 B2  C1C2  0
(11)
Условие параллельности двух плоскостей
Если плоскости  1 и  2 параллельны, то параллельны их нормальные векторы
 
n1 и n2 . Следовательно,
i
 
n1  n2  A1
A2
j
B1
B2
k
C1  0
C2
Отсюда следует, что
A1 B1 C1


.
A2 B2 C2
(12)
162
СЕМИНАР 12.
Пример 1. Найти угол между плоскостью  1 , проходящей через точки A1 2;4;1 ,
A2  1;2;0 , A3 0;2;3 и плоскостью  2 , заданной уравнением 5 x  2 y  3z  1  0 .
Решение. Уравнение плоскости  1 найдем по формуле (9):
x2
y4
z 1
x2
1 2 2  4 0 1  0 ,
0  2  2  4 3 1
3
2
y  4 z 1
1  0 ,
2
6
2
т.е. 7( x  2)  4( y  4)  3( z  1)  0 или 7 x  4 y  3z  1  0 .
По уравнениям плоскостей определим их нормальные векторы: N1  7i  4 j  3k ,
N 2  5i  2 j  3k . Угол  между плоскостями  1 и  2 найдем по формуле (10):
 
n1  n2
A1  A2  B1  B2  C1  C 2
cos     
 0,64 , откуда   arccos 0,64 .
2
n1  n2
A1  B12  C12  A22  B22  C 22
Пример
2.
Найти
уравнение плоскости,

перпендикулярно вектору n ( 2 ; 2 ; 3 ).
проходящей
через
точку
M 0 1;1;1
Решение. В нашем случае A  1 , B  1 и C  1 ; x0  2 , y 0  2 , z 0  3 , следовательно,
уравнение плоскости имеет вид
2  ( x  1)  2  ( y  1)  3  ( z  1)  0, или
2  x  2  y  3  z  7  0.
Или,
окончательно,
искомая
плоскость
определяется
уравнением
2  x  2  y  3  z  7  0.
Пример 3. Написать уравнение плоскости, проходящей через точку
A2;5;3
перпендикулярно вектору BC , если B7;8;1 и C9;7;4 .
Решение. Найдем BC  9  7;7  8;4  1  2;1;5 . Воспользуемся уравнением плоскости,
проходящей
через
заданную
точку:
Ax  x0   B y  y0   C z  z 0   0 .
Имеем
2x  2  1 y  5  5z  3  0  2 x  y  5 z  16  0 .
Пример 4. Найти уравнение плоскости, проходящей через точки M1 1;5;7 , M 2  3;6;3,
M 3  2;7;3 .
Решение. В уравнение плоскости, проходящей через три точки, подставим координаты
данных точек:
163
.
Раскладывая определитель по элементам первой строки, имеем
.
Пример 5. Составить уравнение плоскости, проходящей через точки А(1;3;2) , B(2;1;0) ,
C (4;2;3) .
Решение. Уравнение плоскости, проходящей через точки A( x1 ; y1 ; z1 ) , B( x2 ; y2 ; z 2 ) ,
x  x1
y  y1
z  z1
C ( x3 ; y3 ; z 3 ) имеет вид: x2  x1
y 2  y1
y3  y1
z 2  z1  0 . Тогда уравнение плоскости имеет
z 3  z1
x3  x1
вид
x 1 y  3 z  2
z2
0  2  0 или  3
2
2  0.
3
1
5
23 3 2
x 1 y  3
 2 1 1 3
4 1
Запишем полученное уравнение в общем виде, т.е. в виде Ax  By  Cz  D  0 . Для
этого
раскроем
определитель
( x  1)  (10  2)  ( y  3)  (15  6)  ( z  2)  (3  6)  0 .
по
первой
После
преобразований
строке
получим:
8 x  21y  9 z  37  0 .
Пример 6. Найти нормальный вектор плоскости 2 x  3 y  z  5  0 .
Решение. Нормальный вектор N - это вектор, перпендикулярный плоскости. Если
плоскость задана общим уравнением Ax  By  Cz  D  0 , то нормальный вектор имеет
координаты A, B, C.
Для плоскости
2x  3y  z  5  0
нормальным является вектор
N = 2;3;1.
Отметим, что любой вектор, коллинеарный вектору N = 2;3;1 так же является
нормальным вектором плоскости
2 x  3 y  z  5  0 . Таким образом, при каждом
ненулевом  вектор с координатами 2;3; будет являться нормальным вектором
рассматриваемой плоскости.
Пример 7. Найти косинус угла между плоскостями 2 x  3 y  z  4  0 и x  5 y  4 z  0 .
Решение.
Угол

между
двумя
плоскостями
 1 : A1 x  B1 y  C1 z  D1  0
и
 2 : A2 x  B2 y  C2 z  D2  0 представляет собой угол между их нормальными векторами
и определяется равенством
164
cos  
A1 A2  B1 B2  C1C 2
A  B12  C12  A22  B22  C 22
2
1
Для плоскости 2 x  3 y  z  4  0 координаты нормального вектора N 1  A1 ; B1 ; C1 
определяются равенствами A1  2 , B1  3 , C1  1. Для плоскости x  5 y  4 z  0 равенствами A2  1, B2  5 , C 2  4 . Следовательно,
2  1  (3)  5  1  4
cos  
2  (3) 2  12  12  5 2  4 2
2
=
2  15  4
9
9
9
3 3
.




14
4  9  1  1  25  16
14  42
588
14 3
Пример 8. Составить уравнение плоскости  , проходящей через точку M 0 (1;2;5)
параллельно плоскости  1 : 2 x  3 y  z  5  0 .
Решение. Уравнение плоскости, проходящей через точку M 0 ( x0 ; y0 ; z 0 ) , имеет вид
A( x  x0 )  B( y  y0 )  C ( z  z 0 )  0
Подставим в это уравнение координаты точки M 0 : A( x  1)  B( y  2)  C ( z  5)  0 .
Условие параллельности плоскостей A1 x  B1 y  C1 z  D1  0 и A2 x  B2 y  C2 z  D2  0
имеет вид
A1 B1 C1
. Так как плоскости  и  1 параллельны, то в качестве


A2 B2 C 2
нормального вектора N плоскости  можно взять нормальный вектор N1  2;3;1
A B C
 
можно принять равным единице.
2 3 1
плоскости  1 , т.е. в формуле отношение
Следовательно, уравнение плоскости  1 примет вид 2( x  1)  3( y  2)  ( z  5)  0 .
Запишем это уравнение в общем виде: 2 x  3 y  z  9  0 .
Пример 9. Найти расстояние от точки M 0 (1,3,2) до плоскости  : 3 x  2 y  4 z  5  0 .
Решение. Расстояние d от точки M 0 ( x0 ; y0 ; z 0 ) до плоскости  : Ax  By  Cz  D  0
представляет собой длину перпендикуляра, опущенного из точки на плоскость, и
определяется формулой d 
Ax0  By 0  Cz 0  D
A2  B 2  C 2
.
Для плоскости 3 x  2 y  4 z  5  0 координаты нормального вектора N  A; B; C
определяются
d
равенствами
3  1  2  3  4  (2)  5
3  (2)  4
2
2
2

A  3,
 16
9  4  16

B  2 ,
C  4.
Следовательно,
16
.
29
Пример 10. Построить плоскость, заданную общим уравнением: 2 x  3 y  6 z  6  0 .
165
Решение. Преобразуем данное уравнение в уравнение в отрезках
2х 3у 6z 6



6
6
6 6
или
х у z
   1.
3 2 1
Видим, что плоскость отсекает на осях Ox , Oy , Oz , соответственно отрезки 3, 2, 1.
Следовательно, она проходит через точки M 1 3;0;0 , M 2 0;2;0 , M 3 0;0;1 . По этим
данным легко построить плоскость (см. рисунок).
Пример 11. Составить уравнение плоскости  , проходящей через точку M 1  1;2;5
параллельно плоскости  2 : 2 x  3 y  5  0 .
Решение. Нормальный вектор n 2;3;0 плоскости  2 является также нормальным
вектором плоскости  1 . Получаем: 2( x  1)  3( y  2)  0( z  5)  0 – уравнение плоскости
 1 по точке и нормальному вектору. Раскрывая скобки и приводя подобные слагаемые,
найдем 2 x  3 y  8  0 – общее уравнение плоскости.
166
ЛЕКЦИЯ 13. Уравнения прямой в пространстве. Взаимное расположение прямой и
плоскости в пространстве.
Каноническое уравнение прямой.
Прямая
L
в пространстве однозначно определяется точкой
M 0  x0 ; y 0 ; z 0  и
направлением, т.е. некоторым вектором, называемым направляющим. Пусть дана какаянибудь прямая L , точка M 0 x0 ; y 0 ; z 0 , ей принадлежащей и вектор al; m; n ей
коллинеарным (рис.1).
Рис. 1.
Пусть M x; y; z  - произвольная точка на прямой L . Тогда координаты вектора
M 0 M будут x  x0 ; y  y 0 ; z  z 0  и вектор M 0 M параллелен al; m; n . Следовательно,
Тогда прямая определяется уравнениями:
x  x0 y  y 0 z  z 0


l
m
n
(1)
Параметрическое уравнение прямой.
Введем параметр t
x  x o y  yo z  zo


t,
m
n
p
Получим параметрическое уравнение прямой линии в пространстве.
 x  mt  xo

 y  nt  yo
 z  pt  z
o

(2)
167