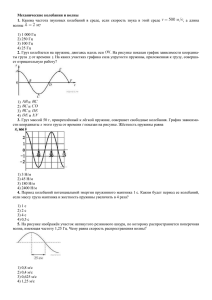
Лабораторная работа №2. «Изучение колебаний пружинного

Лабораторная работа №2.
«Изучение колебаний пружинного маятника».
Цель работы: изучить колебания пружинного маятника без учёта массы пружины.
Задачи работы:
1. Экспериментально исследовать колебания пружинного маятника:
1.1. Проверка гипотезы: если массу груза увеличить в 4 раза, то период колебаний
пружинного маятника увеличится в 2 раза.
1.2.Исследовать период колебаний пружинного маятника с применением графической
обработки экспериментальных данных: 1) построение графической зависимости T=f(m)
и расчёт жёсткости пружины; 2) построение графической зависимости T  f ( m ) и
расчёт жёсткости пружины.
2. Экспериментально применить пружинный маятник для расчёта жёсткости пружины с
оценкой погрешности измерения.
3. Экспериментально применить пружинный маятник для определения периода колебаний.
Оборудование: штатив, муфта, лапка, пружина, набор грузов, секундомер, линейка.
рис. 1
1
Экспериментальное исследование колебаний пружинного маятника
Для экспериментального исследования колебаний пружинного маятника, проверки гипотез,
графической обработки экспериментальных данных использовать экспериментальную установку,
изображённую на рисунке 1.
Для проверки гипотезы «Если массу груза увеличить в 4 раза, то период колебаний
пружинного маятника увеличится в 2 раза» подготовить таблицу измерений и вычислений:
№
опыта
Число
колебаний
1
2
3
20
20
20
Масса груза
m1=100 г (50 г)
Период
Время
колебаний
t
T
с
с
Среднее
Масса груза
m2=400 г (200 г)
Период
Время
колебаний
t
T
с
с
Tср 
Tср 
Среднее
Исследовать период колебаний пружинного маятника с применением графической
обработки экспериментальных данных:
1) построить графическую зависимость T=f(m) в Microsoft Excel, используя мастер
диаграмм с добавлением линии тренда и указанием уравнения кривой; сравнивая полученное
уравнение графической зависимости периода колебаний пружинного маятника с формулой
T  2 
m
, рассчитать жёсткость пружины:
k
Число колебаний
Время
Масса груза
Масса груза
Период колебаний
N
t
m
m
T
с
г
кг
с
20
50
20
20
20
20
20
20
20
100 150 200 250 300 350 400
2) построить графическую зависимость T  f ( m ) в Microsoft Excel, используя мастер
диаграмм с добавлением линии тренда и указанием уравнения кривой; сравнивая полученное
уравнение графической зависимости периода колебаний пружинного маятника с формулой
T  2 
m
, рассчитать жёсткость пружины:
k
Число колебаний
Время
Масса груза
Масса груза
м.груза
Период
колебаний
N
t
m
m
с
г
кг
m
кг
T
с
20
50
20
20
20
20
20
20
20
100 150 200 250 300 350 400
2
Экспериментальное применение пружинного маятника
для расчёта жёсткости пружины с оценкой погрешности измерения
Способ 1
Ход работы:
1. Собрать экспериментальную установку для косвенного измерения жёсткости пружины при
помощи пружинного маятника.
2. Подготовить таблицу измерений и вычислений:
Число
колебаний
N
20
20
20
20
20
№
опыта
1
2
3
4
5
Время
t
c
Период
колебаний
T
c
Абсолютная
погрешность
T
c
Среднее
3. При фиксированной массе груза (m=300 г=0,3 кг):

измерить время 20 полных колебаний;

рассчитать период колебаний;

дополнительно провести серию из 4 опытов;
n
T
i
Т 1  Т 2  ...  Т 5
;
5

рассчитать среднее значение периода колебаний Tср 

определить абсолютную погрешность периода колебаний Ti  Tср  Ti ;

рассчитать
среднее
i 1
n

значение абсолютной погрешности
периода колебаний
n
Tср 
 T
i
i 1
n

Т 1  Т 2  ...  Т 5
;
5
4. Записать формулу периода колебаний пружинного маятника T  2 
m
.
k
5. Выразить из неё жёсткость пружины и рассчитать её числовое значение, подставив среднее
значение периода колебаний: k расч 
4 2  m
.
Tср2
6. Рассчитать относительную погрешность косвенного измерения жёсткости пружины при
помощи пружинного маятника (т.к. , то 0,005; т.к. m=0,3 кг, то m=0,05 кг):
3
k 
  
2
  T    m 
2
2
2
    Tср
 2 
  2
   Tср

7. Определить абсолютную погрешность
2
  m  2
 

  m 

косвенного измерения жёсткости пружины при
помощи пружинного маятника: k  k расч   k 
8. Записать окончательный результат измерения жёсткости пружины в стандартной форме:
k  k расч  k 
Н

м
9. Изобразить на числовой оси доверительный интервал полученных значений косвенного
измерения жёсткости пружины при помощи пружинного маятника.
4
Способ 2
Теоретические основы измерения жёсткости пружины способом 2
Период колебаний пружинного маятника равен T  2 
m
. Если определить период колебаний
k
пружинного маятника Т1 при массе груза m1, а затем увеличить массу и снова определить
период колебаний Т2 при массе груза m2, то можно найти жёсткость пружины следующим
образом:
T1  2 
T2  2 
m1
 k  T12  4 2  m1
k
m2
 k  T22  4 2  m2
k
k
4 2  m2  m1 
T22  T12 
Суть способа 2 состоит в определении периода T колебаний пружинного маятника при
разной массе груза для последующего вычисления жёсткости пружины.
Ход работы:
1. Собрать экспериментальную установку:
2. К пружине подвесить груз массой m1=100 г. Сместить груз из положения равновесия и
привести его в колебательное движение. С помощью секундомера измерить время 20
полных колебаний при данной массе груза. Рассчитать период колебаний по формуле
T1=t1/20.
3. Увеличить массу груза до m2=200 г. Пружинный маятник привести в колебательное
движение. С помощью секундомера измерить время 20 полных колебаний при данной
массе груза. Рассчитать период колебаний по формуле T2=t2/20.
4. Повторить измерения времени 20 полных колебаний для массы груза m3=300 г и m4=400 г.
Рассчитать периоды колебаний T3=t3/20, T4=t4/20. Каждый раз результаты измерений и
вычислений заносить в отчётную таблицу.
5
Масса груза
Время 20 полных колебаний
Период колебаний
m1=100 г=0,1 кг
t1 =
с
T1=t1/20=
c
m2=200 г=0,2 кг
t2 =
c
T2=t2/20=
c
m3=300 г=0,3 кг
t3 =
c
T3=t3/20=
c
m4=400 г=0,4 кг
t4 =
c
T4=t4/20=
c
5. Рассчитать числовые значения жёсткости пружины и оценить погрешность методом
среднего арифметического.
Абсолютная погрешность
Жёсткость пружины, Н/м
k1 
4 2  m2  m1 
T22  T12 
k2 
4 2  m3  m2 
T32  T22 
k3 
4 2  m4  m3 
T42  T32 
k i  k ср  k i
Н
м
Среднее
Относительная погрешность
Ускорение
=
k ср
k ср
 100% 
k= k ср  k ср  Н/м = (

) Н/м
Нижняя граница
НГ(k)= k ср  k ср  Н/м =
Н/м
Верхняя граница
ВГ(k)= k ср  k ср  Н/м =
Н/м
6. Изобразить на числовой оси доверительный интервал полученных значений косвенного
измерения жёсткости пружины.
6
Использование пружинного маятника для определения периода колебаний
Цель работы: экспериментально определить период колебаний пружинного маятника,
сравнить результат с теоретическими расчётами.
Задача работы: сравнение экспериментальных данных по измерению периода колебаний
пружинного маятника с теоретическими расчётами.
Оборудование: набор грузов, стальная пружина, штатив с лапкой и муфтами, секундомер,
линейка с миллиметровыми делениями.
Содержание и метод выполнения работы:
Груз, подвешенный на стальной пружине и выведенный из положения равновесия,
совершает под действием сил тяжести и упругости пружины свободные гармонические колебания.
Период колебаний такого пружинного маятника определяется выражением T  2
m
, где k 
k
жёсткость пружины, m  масса тела. Задача данной работы заключается в том, чтобы
экспериментально проверить полученные теоретически результаты. Для решения этой задачи
сначала необходимо определить жёсткость пружины, применяемой в лабораторной установке
k
mg
, где х0  удлинение пружины под действием груза массой т. Т.е. период колебаний
x0
пружинного маятника может быть представлен в виде: T  2
x0
. Затем теоретически
g
необходимо произвести расчёт периода колебаний пружинного маятника с грузом фиксированной
массой m =300 г=0,3 кг. Далее в эксперименте определяется период колебаний пружинного
маятника и сравнивается с теоретическим значением.
Ход работы:
1. Собрать экспериментальную установку.
2. К свободному концу пружины подвесить груз фиксированной массой m =300 г=0,3 кг и
измерить х0  удлинение пружины под действием груза массой т.
7
3. По данным значениям m, х0 рассчитать теоретическое значение периода колебаний
x0
g
пружинного маятника по формуле: Tтеор  2
4. Абсолютные погрешности постоянных, входящих в формулу периода колебаний: 1) для
ускорения свободного падения g=9,8 м/с2, g=0,05 м/с2; 2) , 0,005.
5. Рассчитать полную абсолютную погрешность измерения длины с учетом погрешности
прибора и погрешности отсчёта. Учитывать, что измерительная лента лишена класса
точности, поэтому абсолютная погрешность прибора принимается равной половине цены
деления наименьшего значения шкалы прибора, абсолютная погрешность отсчёта также
равна половине цены деления прибора: x0  2 прибора  2отсчёта
6. Рассчитать относительную погрешность косвенного измерения теоретического периода
колебаний пружинного маятника по формуле:
T
теор

  
2
 
  g    x0
2
2
2
2
    1 g   1 x0 
 
 
   
   
    2 g   2 x0 
2
7. Рассчитать абсолютную погрешность косвенного измерения теоретического периода
колебаний пружинного маятника по формуле: Tтеор  Т теор   Ттеор 
8. Окончательный результат косвенного измерения теоретического периода колебаний
пружинного маятника представить в стандартной форме: Т  Т теор  Т теор с 
9. Для экспериментального расчёта периода колебаний пружинного маятника с массой груза
m =300 г=0,3 кг измерить время 20 полных колебаний и рассчитать экспериментальный
период колебаний. Провести общую серию из 5 опытов и обработать полученные значения
методом среднего арифметического. Результаты измерений и вычислений оформить в
отчётной таблице:
№
опыта
1
2
3
4
5
Число
колебаний
N
20
20
20
20
20
Время
t
с
Период
колебаний
T
с
Абсолютная
погрешность
T
с
Среднее
8
n
Tср 
 Ti
i 1
n
n
Т  Т 2  ...  Т 5
Т i  Т ср  Т i Tср 
 1
5
,
,
Т ср
 T
i
i 1
n
Относительная погрешность
=
Экспериментальный период
колебаний пружинного
маятника
Тэксп= Т ср  Т ср  с = (
Т ср

Т 1  Т 2  ...  Т 5
5
 100% 

)с
Нижняя граница
НГ(Тэксп)= Т ср  Т ср  с =
с
Верхняя граница
ВГ(Тэксп)= Т ср  Т ср  с =
с
10. На одной числовой оси изобразить доверительные интервалы периодов колебаний
пружинного маятника рассчитанного теоретически (пункт 8) и экспериментально (пункт 9)
и сформулировать вывод.
9