Лабораторная работа №1. «Изучение треков заряженных
реклама
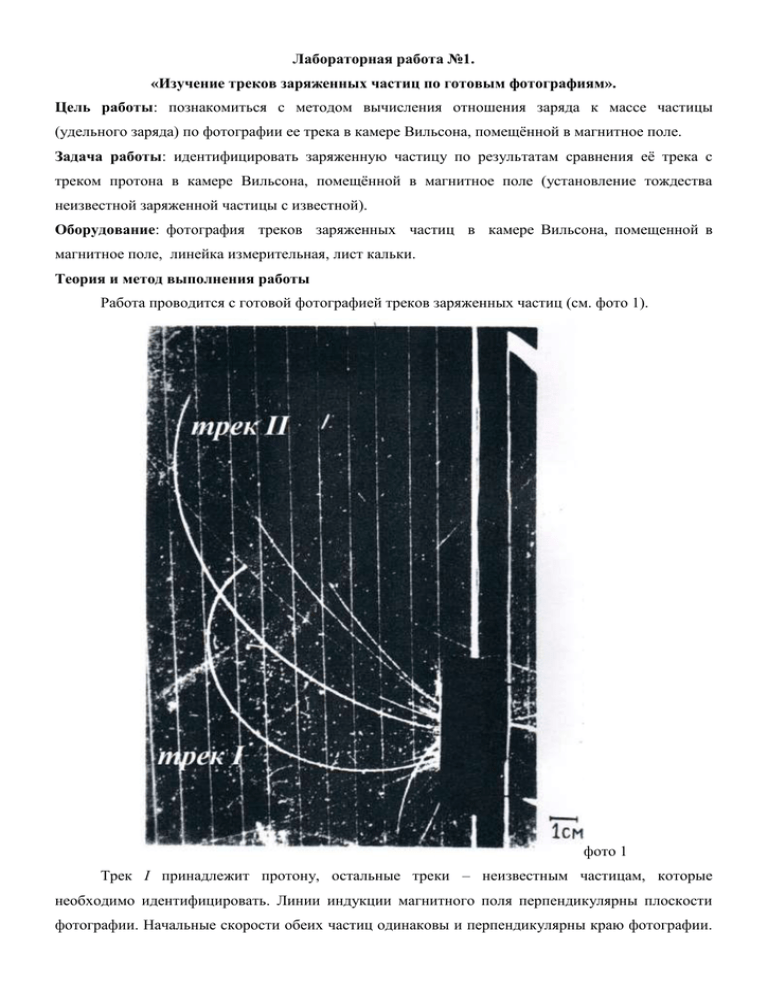
Лабораторная работа №1. «Изучение треков заряженных частиц по готовым фотографиям». Цель работы: познакомиться с методом вычисления отношения заряда к массе частицы (удельного заряда) по фотографии ее трека в камере Вильсона, помещённой в магнитное поле. Задача работы: идентифицировать заряженную частицу по результатам сравнения её трека с треком протона в камере Вильсона, помещённой в магнитное поле (установление тождества неизвестной заряженной частицы с известной). Оборудование: фотография треков заряженных частиц в камере Вильсона, помещенной в магнитное поле, линейка измерительная, лист кальки. Теория и метод выполнения работы Работа проводится с готовой фотографией треков заряженных частиц (см. фото 1). фото 1 Трек I принадлежит протону, остальные треки – неизвестным частицам, которые необходимо идентифицировать. Линии индукции магнитного поля перпендикулярны плоскости фотографии. Начальные скорости обеих частиц одинаковы и перпендикулярны краю фотографии. Идентификация неизвестной частицы осуществляется путём сравнения её удельного заряда с удельным зарядом протона. Это осуществляется путём измерения радиусов треков частиц на начальных участках треков: 1) вычерчивают две хорды (см. рис. 1) и восставляют к этим хордам в их серединах перпендикуляры, на пересечении которых, лежит центр окружности; её радиус на начальном участке трека измеряют линейкой (см. рис. 2); Рис. 1 Рис. 2 2) вычерчивают хорду длиной l на начальном участке трека и восставляют в её середину с внутренней поверхности дуги окружности перпендикуляр h (см. рис. 3); радиус окружности l 2 4h 2 на начальном участке трека вычисляют по формуле R . 8h Рис. 3 Ход работы: 1. Решить задачу: в поперечное однородное магнитное поле с одной и той же скоростью в одном и том же направлении влетают две заряженные частицы; чему равно отношение удельных зарядов этих частиц, если радиусы кривизны их траекторий оказались равными R1 и R2. Правильным ответом является выражение, в котором отношение удельных зарядов частиц равно обратному отношению радиусов их траекторий в магнитном поле. 2. Перенести на кальку треки частиц с фотографии. Трек I принадлежит протону. Измерить радиусы кривизны треков заряженных частиц, скопированных на кальку, на их начальных участках. Для измерения радиуса выбрать один из двух способов описанных в теории и методе выполнения работы. 3. Сравнить удельные заряды неизвестной частицы и протона. Идентифицировать частицу по результатам измерений и вычислений, используя справочный материал: Название частицы электрон протон -частица тритон q Кл , m кг -1,76∙1011 9,56∙107 4,82∙107 3,19∙107 4. Результаты измерений и вычислений оформить в виде таблицы: Радиус I трека (протона) Абсолютная погрешность (цена деления линейки) Радиус I трека (протона) R1изм= мм R= мм R1=( R1изм±R)мм=( Удельный заряд протона q1 Кл 9,56 107 m1 кг Абсолютная погрешность q Кл 1 0,005 107 кг m1 Радиус II трека (неизвестной частицы) Абсолютная погрешность (цена деления линейки) Радиус II трека (неизвестной частицы) R2изм= мм R= мм R2=( R2изм±R)мм=( Удельный заряд неизвестной частицы q2 q R 1 1изм m2 расч m1 R2 изм Относительная погрешность q2 m2 ± ± ) мм ) мм q1 m1 R R q1 R1 R2 m1 Абсолютная погрешность q q 2 2 q2 m2 m2 расч m2 Удельный заряд неизвестной частицы q q2 q2 2 m2 m2 расч m2 Идентификация неизвестной частицы Числовая ось Кл кг Кл кг Кл кг






