MI_Algebra - Владимирский государственный университет

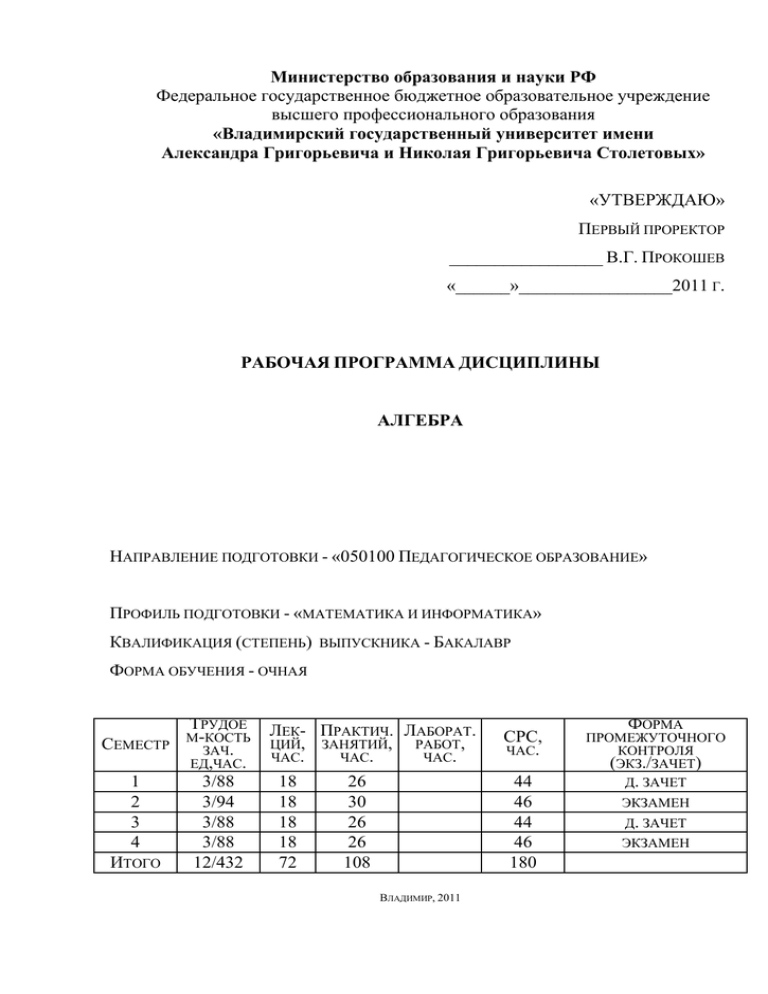
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Владимирский государственный университет имени
Александра Григорьевича и Николая Григорьевича Столетовых»
«УТВЕРЖДАЮ»
ПЕРВЫЙ ПРОРЕКТОР
_________________ В.Г. ПРОКОШЕВ
«______»_________________2011 Г.
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
АЛГЕБРА
НАПРАВЛЕНИЕ ПОДГОТОВКИ - «050100 ПЕДАГОГИЧЕСКОЕ ОБРАЗОВАНИЕ»
ПРОФИЛЬ ПОДГОТОВКИ - «МАТЕМАТИКА И ИНФОРМАТИКА»
КВАЛИФИКАЦИЯ (СТЕПЕНЬ)
ВЫПУСКНИКА - БАКАЛАВР
ФОРМА ОБУЧЕНИЯ - ОЧНАЯ
СЕМЕСТР
1
2
3
4
ИТОГО
ТРУДОЕ
М-КОСТЬ
ЗАЧ.
ЕД,ЧАС.
3/88
3/94
3/88
3/88
12/432
ЛЕК- ПРАКТИЧ. ЛАБОРАТ.
ЦИЙ, ЗАНЯТИЙ,
РАБОТ,
ЧАС.
ЧАС.
ЧАС.
18
18
18
18
72
26
30
26
26
108
СРС,
ЧАС.
44
46
44
46
180
ВЛАДИМИР, 2011
ФОРМА
ПРОМЕЖУТОЧНОГО
КОНТРОЛЯ
(ЭКЗ./ЗАЧЕТ)
Д. ЗАЧЕТ
ЭКЗАМЕН
Д. ЗАЧЕТ
ЭКЗАМЕН
1. ЦЕЛИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
ЦЕЛЯМИ ОСВОЕНИЯ ДИСЦИПЛИНЫ (МОДУЛЯ)
ЯВЛЯЮТСЯ
ИЗУЧЕНИЕ
ОСНОВНЫХ
АЛГЕБРАИЧЕСКИХ СТРУКТУР И ПРИВИВАНИЕ ОБЩЕЙ АЛГЕБРАИЧЕСКОЙ КУЛЬТУРЫ, НЕОБХОДИМОЙ
ДЛЯ ДАЛЬНЕЙШЕГО ИЗУЧЕНИЯ УНИВЕРСИТЕТСКИХ МАТЕМАТИЧЕСКИХ И ФИЗИЧЕСКИХ ДИСЦИПЛИН
И ОБЕСПЕЧИВАЮЩИХ БУДУЩЕМУ УЧИТЕЛЮ ГЛУБОКОЕ ПОНИМАНИЕ ОСНОВ ШКОЛЬНОГО КУРСА
МАТЕМАТИКИ.
ЦЕЛИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ:
 ПОЗНАКОМИТЬ СТУДЕНТОВ С КРУГОМ ЗАДАЧ КЛАССИЧЕСКОЙ И СОВРЕМЕННОЙ АЛГЕБРЫ;
 ПРОЯСНИТЬ РОЛЬ АЛГЕБРАИЧЕСКИХ ПОНЯТИЙ ВО ВЗАИМОСВЯЗИ С ДРУГИМИ
МАТЕМАТИЧЕСКИМИ ДИСЦИПЛИНАМИ;
 СФОРМИРОВАТЬ У СТУДЕНТОВ ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ КУЛЬТУРЫ, КОТОРЫЕ
СМОГУТ ОБЕСПЕЧИТЬ ЯСНОЕ ПОНИМАНИЕ СМЫСЛА И ЗНАЧЕНИЯ РАЗДЕЛОВ МАТЕМАТИКИ,
ИЗУЧАЕМЫХ В ШКОЛЕ;
ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ:
 НАУЧИТЬ СТУДЕНТОВ ПРОЯВЛЯТЬ
САМОСТОЯТЕЛЬНОСТЬ И ТВОРЧЕСКИЙ ПОДХОД В
ОВЛАДЕНИИ МАТЕМАТИЧЕСКИМИ ДИСЦИПЛИНАМИ;

НАУЧИТЬ СТУДЕНТОВ ОПЕРИРОВАТЬ С КЛАССИЧЕСКИМИ ПОНЯТИЯМИ АЛГЕБРЫ: РЕШАТЬ
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ, РЕШАТЬ ЗАДАЧИ, СВЯЗАННЫЕ С
ЛИНЕЙНОЙ ЗАВИСИМОСТЬЮ И ЛИНЕЙНОЙ НЕЗАВИСИМОСТЬЮ СИСТЕМЫ ВЕКТОРОВ, ЗАДАЧИ,
СВЯЗАННЫЕ С ПРИВОДИМОСТЬЮ И НЕПРИВОДИМОСТЬЮ МНОГОЧЛЕНОВ НАД РАЗЛИЧНЫМИ
ЧИСЛОВЫМИ ПОЛЯМИ;

НА ПРИМЕРЕ ТЕМЫ «ГРУППЫ. КОЛЬЦА. ПОЛЯ » ПОЗНАКОМИТЬ СТУДЕНТОВ С РАЗДЕЛАМИ
СОВРЕМЕННОЙ АЛГЕБРЫ И РАССМОТРЕТЬ НЕКОТОРЫЕ ЗАДАЧИ ИЗ ЭТИХ РАЗДЕЛОВ.
2. МЕСТО ДИСЦИПЛИНЫ В СТРУКТУРЕ ООП
ДИСЦИПЛИНА ОТНОСИТСЯ К ПРОФЕССИОНАЛЬНОМУ ЦИКЛУ. С КУРСА АЛГЕБРЫ
И ТЕОРИИ ЧИСЕЛ НАЧИНАЕТСЯ МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ. ЕЕ ИЗУЧЕНИЕ
ОСНОВЫВАЕТСЯ НА ТАКИХ МАТЕМАТИЧЕСКИХ ПОНЯТИЯХ, КАК МНОЖЕСТВО,
МНОГОЧЛЕН, ФУНКЦИЯ, РАССМАТРИВАЕМЫХ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ, И
ПРОДОЛЖАЕТ РАЗВИТИЕ ИДЕЙ И МЕТОДОВ ДАННОГО КУРСА. ПОЭТОМУ ДЛЯ
УСПЕШНОГО УСВОЕНИЯ КУРСА «АЛГЕБРА» НЕОБХОДИМО ЗНАНИЕ ОСНОВНЫХ
ФОРМУЛ, ИЗУЧАЕМЫХ В ШКОЛЬНОЙ АЛГЕБРЕ, СВОЙСТВ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ,
УМЕНИЕ РЕШАТЬ КВАДРАТНЫЕ УРАВНЕНИЯ, ЗНАНИЕ ОСНОВНЫХ ЗНАЧЕНИЙ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
КУРС «АЛГЕБРА» ИМЕЕТ СВЯЗИ С РАЗЛИЧНЫМИ МАТЕМАТИЧЕСКИМИ
ДИСЦИПЛИНАМИ. ЗНАНИЯ, ПОЛУЧЕННЫЕ В ЭТОМ КУРСЕ, ИСПОЛЬЗУЮТСЯ В
АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ, МАТЕМАТИЧЕСКОМ АНАЛИЗЕ, ФУНКЦИОНАЛЬНОМ
АНАЛИЗЕ, ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ И ТОПОЛОГИИ, ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЯХ, ДИСКРЕТНОЙ МАТЕМАТИКЕ И МАТЕМАТИЧЕСКОЙ ЛОГИКЕ, ТЕОРИИ
ЧИСЕЛ, МЕТОДАХ ОПТИМИЗАЦИИ И ДР. ТАК РАЗДЕЛ «ЛИНЕЙНЫЕ ВЕКТОРНЫЕ
ПРОСТРАНСТВА» ТЕСНО СВЯЗАН С КУРСОМ «ГЕОМЕТРИЯ», КОТОРЫЙ ДАЕТ ДЛЯ
ДАННОГО РАЗДЕЛА МНОГОЧИСЛЕННЫЕ ПРИМЕРЫ. В СВОЮ ОЧЕРЕДЬ ГЕОМЕТРИЯ
АКТИВНО ИСПОЛЬЗУЕТ ПОНЯТИЯ ЛИНЕЙНО-ЗАВИСИМОЙ И ЛИНЕЙНО-НЕЗАВИСИМОЙ
СИСТЕМЫ
ВЕКТОРОВ,
КОТОРЫЕ
ИЗУЧАЮТСЯ
В
КУРСЕ
АЛГЕБРЫ.
УМЕНИЕ
ОПЕРИРОВАТЬ КОМПЛЕКСНЫМИ ЧИСЛАМИ И ЗНАНИЕ ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЫ
«ТЕОРИЯ
ГРУППЫ, КОЛЬЦА, ПОЛЯ,
КОМПЛЕКСНОГО ЧИСЛА НЕОБХОДИМЫ ДЛЯ ИЗУЧЕНИЯ КУРСА
КОМПЛЕКСНОГО ПЕРЕМЕННОГО».
ПОНЯТИЕ
ФУНКЦИЙ
А ТАКЖЕ
ПОНЯТИЯ ГОМОМОРФИЗМА И ИЗОМОРФИЗМА АЛГЕБРАИЧЕСКИХ СИСТЕМ АКТИВНО
ИСПОЛЬЗУЮТСЯ В КУРСЕ «ЧИСЛОВЫЕ СИСТЕМЫ».
3. КОМПЕТЕНЦИИ ОБУЧАЮЩЕГОСЯ, ФОРМИРУЕМЫЕ В РЕЗУЛЬТАТЕ
ОСВОЕНИЯ ДИСЦИПЛИНЫ (МОДУЛЯ)
В результате освоения дисциплины обучающийся должен демонстрировать следующие
результаты образования: ОК-1,4,6; ОПК-3,4; ПК-5,6,11,13
Выпускник должен обладать следующими общекультурными компетенциями (ОК):
владением культурой мышления, способностью к обобщению, анализу, восприятию
информации, постановке цели и выбору путей её достижения (ОК-1);
способностью использовать знания о современной естественнонаучной картине мира
в образовательной и профессиональной деятельности, применять методы математической
обработки информации, теоретического и экспериментального исследования (ОК-4);
способностью логически верно выстраивать устную и письменную речь (ОК-6);
Выпускник должен обладать следующими профессиональными компетенциями (ПК):
владением основами речевой профессиональной культуры (ОПК-3);
способностью нести ответственность за результаты своей профессиональной
деятельности (ОПК-4);
в области педагогической деятельности:
способностью использовать возможности образовательной среды для формирования
универсальных видов учебной деятельности и обеспечения качества учебно-воспитательного
процесса (ПК-5);
готовностью к взаимодействию с учениками, родителями, коллегами, социальными
партнерами (ПК-6);
готовностью использовать систематизированные теоретические и практические
знания для определения и решения исследовательских задач в области образования (ПК-11);
способностью использовать в учебно-воспитательной деятельности основные методы
научного исследования (ПК-13).
В результате курса алгебры студент должен знать следующие методы, факты, свойства,
применяемые при решении алгебраических задач
Алгебры, алгебраические системы.
1. Умение определять характеристики множества (группа, кольцо, поле)
2. Умение работать в кольце классов вычетов.
Системы линейных уравнений. Определители.
1. Владение общими приемами при решении систем линейных уравнений
2. Применение метода последовательного исключения неизвестных.
3. Вычисление определителей произвольного порядка.
4. Знание теоремы Лапласа и ее применение для вычисления определителей.
5. Использование правила Крамера для решения систем лин. уравнений общего вида.
Поле комплексных чисел.
1. Умение приводить к тригонометрической форме комплексных чисел.
2. Владение формулой Муавра.
3. Извлечение корней из комплексных чисел.
Арифметические пространства и линейные уравнения.
1. Умение определять базис и ранг конечной системы векторов.
2. Элементарные преобразования матриц.
3. Применения критерия совместности системы линейных уравнений.
4. Знание свойств решений систем линейных уравнений.
Алгебра матриц
1. Применение операций над матрицами.
2. Вычисление обратной матрицы
3. Нахождение ранга матрицы
4. Записи и решение квадратных систем линейных уравнений в матричной форме.
Векторные пространства.
1. Умение определять базис, размерность векторного пространства и координаты
векторов.
2. Определять изоморфизм векторных пространств.
3. Решение неравенства Коши – Буняковского и определения угла между векторами.
Линейные преобразования.
1. Выделение ядра и образа линейного оператора.
2. Умение определять матрицу оператора в различных базисах.
3. Нахождение собственных векторов и значений линейных операторов.
Кольцо многочленов от одной переменной. Теория делимости.
1. Деление на двучлен х – a и корни многочлена.
2. Применение алгоритма Евклида для многочленов.
3. Разложение многочленов на неприводимые множители.
4. Применение формул Виета для решения уравнений произвольной степени.
5. Решение уравнений третьей и четвертой степени.
6. Вычисление целых и рациональные корни многочленов. Критерий неприводимости
Эйзенштейна.
Многочлены от нескольких переменных.
1. Владение всеми способами выражение симметрического многочлена через основные
симметрические.
2. Умение использовать связь симметрических многочленов и формул Виета.
3. Вычисление результанта и дискриминанта многочлена.
Алгебраические числа.
1. Освобождение знаменателя от иррациональности с помощью алгебраических чисел
2. Геометрические построения циркулем и линейкой и разрешимость уравнений в
радикалах. Построение правильных многоугольников.
Группы. Подгруппы.
1. Построение циклической группы.
2. Определение изоморфизма и гомоморфизма групп.
3. Выделение смежных классов.
4. Определенеи различных элементов в фактор-группе.
Кольца. Подкольца.
1. Знание основных свойств кольца и умение применять их к множествам
2. Нахождение идеалов колец, фактор-кольца.
3. Умение находить разложение многочленов на неприводимые множители в кольце
многочленов.
4. СТРУКТУРА И СОДЕРЖАНИЕ ДИСЦИПЛИНЫ (МОДУЛЯ) _______________
1
2
3
4
Объем
Формы
учебной
текущего
работы,
контроля
с
успеваемости
применением
(по неделям
интерактивн
семестра) ,
ых методов
форма
(в часах / %)
промежуточной
аттестации
(по семестрам)
КП / КР
Контрольные
работы,
коллоквиумы
СРС
Лабораторные
работы
Практические
занятия
Семинары
Виды учебной работы, включая
самостоятельную работу студентов
и трудоемкость (в часах)
Лекции
Раздел (тема)
дисциплины
Неделя семестра
№
п/п
Семестр
Общая трудоемкость дисциплины составляет _12____ зачетных единиц, ___432__ часа.
8
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
6
10
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
2
4
6
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
Алгебры,
алгебраическ
ие системы.
Понятия
группы,
кольца, поля.
Кольца
классов
вычетов
Системы
линейных
уравнений.
Определител
и.
Метод
последователь
ного
исключения
неизвестных
Определители
произвольного
порядка
1
4
1
4
1
Теорема
Лапласа.
Правило
Крамера
1
4
Поле
комплексных
чисел.
Тригонометри
ческая форма
комплексных
чисел
Формула
Муавра
1
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
1
2
2
4
7
Корни
из
комплексных
чисел
и
многочлены
деления круга.
1
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
8
Арифметическ
ие
пространства
и
линейные
уравнения
Элементарны
е
преобразован
ия матриц
Критерий
совместности
системы
линейных
уравнений.
Свойства
решений
систем
линейных
уравнений.
2
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
2
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
2
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
2
2
4
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
Алгебра
матриц
Операции над
матрицами.
Вычисление
обратной
матрицы
Определитель
произведения
матриц.
Теорема
о
ранге матрицы
Записи
и
решение
квадратных
систем
линейных
уравнений в
2
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
2
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
2
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
5
6
9
10
11
12
13
14
матричной
форме.
15
Линейные
преобразован
ия.
Ядро и образ
линейного
оператора.
Матрица
линейного
оператора.
2
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
16
Матрица
оператора
в
различных
базисах.
Собственные
вектора
и
значения
линейных
операторов.
2
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
17
Кольцо
многочленов
от
одной
переменной.
Теория
делимости.
Деление
на
двучлен х – a
и
корни
многочлена.
Теорема Безу.
3
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
18
Деление
с
остатком
и
алгоритм
Евклида.
Разложение
многочленов
на
неприводимые
множители
Алгебраическа
я замкнутость
поля
комплексных
чисел.
Формулы
Виета
Уравнения
третьей
и
четвертой
3
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
3
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
3
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
19
20
степени.
Целые
и
рациональные
корни
многочленов.
Критерий
неприводимос
ти
Эйзенштейна.
Рациональные
дроби;
разложение на
простейшие
дроби
Многочлены
от
нескольких
переменных.
Основная
теорема
о
симметрическ
их
многочленах.
3
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
3
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
Симметрическ
ие
многочлены и
формулы
Виета
Результант.
Дискриминант
многочлена
3
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
3
2
2
4
25
Алгебраическ
ие числа.
Простое
алгебраическо
е расширение
поля.
3
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
26
Геометрическ
ие построения
циркулем
и
линейкой
и
разрешимость
уравнений в
радикалах.
Построение
правильных
многоугольни
ков
Группы.
Подгруппы.
Циклические
4
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
21
22
23
24
27
28
29
30
31
32
33
34
группы
Изоморфизмы
и
гомоморфизм
ы групп.
Смежные
классы
и
теорема
Лагранжа.
Факторгруппы.
Действие
трупп
на
множествах;
теорема
Бернсайда.
Образующие и
определяющие
соотношения.
Кольца.
Подкольца.
Кольца целых
чисел,
многочленов и
вычетов.
Евклидовы
кольца.
Кольцо целых
гауссовых
чисел.
Идеалы колец,
факторкольца.
Кольцо
главных
идеалов.
Евклидовы и
факториальны
е кольца.
Факториально
сть
кольца
многочленов.
Разложение
многочленов
на
неприводимые
множители
Кольца
с
неоднозначны
м
разложением
на
простые
множители
КОНТРОЛЬНАЯ
4
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
4
6
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
4
2
2
4
ПРОВЕРКА
ДОМАШНЕГО
ЗАДАНИЯ,
КОНТРОЛЬНАЯ
Всего
5.
72
108
180
ОБРАЗОВАТЕЛЬНЫЕ ТЕХНОЛОГИИ
АКТИВНЫЕ И ИНТЕРАКТИВНЫЕ ФОРМЫ, ЛЕКЦИИ, ПРАКТИЧЕСКИЕ ЗАНЯТИЯ,
КОНТРОЛЬНЫЕ РАБОТЫ, КОЛЛОКВИУМЫ, ЗАЧЕТЫ И ЭКЗАМЕНЫ, КОМПЬЮТЕРЫ. В
ТЕЧЕНИЕ СЕМЕСТРА СТУДЕНТЫ РЕШАЮТ ЗАДАЧИ, УКАЗАННЫЕ ПРЕПОДАВАТЕЛЕМ, К
КАЖДОМУ СЕМИНАРУ. В КАЖДОМ СЕМЕСТРЕ ПРОВОДЯТСЯ КОНТРОЛЬНЫЕ РАБОТЫ
(НА СЕМИНАРАХ). ЗАЧЕТ ВЫСТАВЛЯЕТСЯ ПОСЛЕ РЕШЕНИЯ ВСЕХ ЗАДАЧ
КОНТРОЛЬНЫХ РАБОТ И САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО
ЗАДАНИЯ.
6. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ТЕКУЩЕГО КОНТРОЛЯ УСПЕВАЕМОСТИ, ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ИТОГАМ ОСВОЕНИЯ
ДИСЦИПЛИНЫ
И
УЧЕБНО-МЕТОДИЧЕСКОЕ
ОБЕСПЕЧЕНИЕ
САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
КОНТРОЛЬНЫЕ, КОЛЛОКВИУМЫ ОЦЕНИВАЮТСЯ ПО ПЯТИБАЛЛЬНОЙ СИСТЕМЕ.
ЭКЗАМЕНЫ ОЦЕНИВАЮТСЯ ПО СИСТЕМЕ: НЕУДОВЛЕТВОРИТЕЛЬНО,
УДОВЛЕТВОРИТЕЛЬНО, ХОРОШО, ОТЛИЧНО. НА ПРАКТИЧЕСКИХ ЗАНЯТИЯХ КОНТРОЛЬ
ОСУЩЕСТВЛЯЕТСЯ ПРИ ОТВЕТЕ У ДОСКИ И ПРИ ПРОВЕРКЕ ДОМАШНИХ ЗАДАНИЙ. НА
КАФЕДРЕ СОЗДАНА ПРОГРАММА, ГЕНЕРИРУЮЩАЯ ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО
МАТЕРИАЛАМ 1, 2, 3, 4 СЕМЕСТРОВ.
Формы текущего промежуточного и итогового контроля
Семестр 1
Контрольная работа № 1.
Тема«Системы лин.уравнений;, оперделители».
Решить систему лин. уравнений по методу Гаусса.
Решить систему лин. уравнений по правилу Крамера.
Вычислить определитель, применив теорему Лапласа.
Выяснить совместность системы лин. уравнений при различных значениях параметра
а.
5. Вычисление определителя N-порядка.
1.
2.
3.
4.
Контрольная работа № 2.
Тема«Комплексные числаи».
1.
2.
3.
4.
5.
Представить комплексные числа в тригонометрической форме.
Выполнить арифметические действия с комплексными числами
Связь комплексных чисел с геометрией на плоскости.
Доказать тождество.
Извлечь корни из комплексных чисел.
Коллоквиум.
1. Примеры колец классов вычетов.
2. Подстановки. Четность и знак подстановки.
3. Определитель Вандермонда.
Семестр 2
Контрольная работа № 1.
Тема«Матрицы;фундаментальный набор решений».
1.
2.
3.
4.
5.
Определить ранг матрицы изученными способами.
Решить систему лин. уравнений в матричном виде.
Найти обратную матрицу с помощью алгебраических дополнений.
Найти обратную матрицу с помощью единичной матрицы.
Найти фундаментальную систему решений однородной системы .
Контрольная работа № 2.
Тема«Векторные простанства»
1.
2.
3.
4.
Найти базис пространства.
Найти координаты вектора в заданном базисе.
Найти максимально линейно независимую подсистему системы векторов.
Ортогонализировать систему векторов.
Коллоквиум.
1. вычисление сумм и произведений с помощью комплексных чисел
2. Связь комплексных чисел с геометрией на плоскости.
3. Теорема о ранге матрицы.
Семестр 3
Контрольная работа № 1.
Тема«Линейные преобразования; собственные значения и вектора».
1. Найти ядро и образ данного линейного оператора.
2. Найти матрицу линейного оператора в новом базисе.
3. Найти собственные значения и собственные вектора для данного линейного
оператора.
Контрольная работа № 2.
Тема«Многочлены от одной переменной; формулы Виета».
1.
2.
3.
4.
5.
Отделить кратные корни многочлена.
Разложить многочлен по степеням одночлена.
Разложить многочлен на неприводимоые множители.
Найти рациональные корни многчлена.
Найти неизвестный коэффициент многочлена , зная его корни (формулы Виета).
Коллоквиум.
1. Изоморфизм векторных пространств.
2. Подпространство, ортогональное к данному.
3. Линейные операторы с простым спектром
Семестр 4
Контрольная работа № 1.
Тема«Многочлены от нескольких переменных ;решение систем».
1.
2.
3.
4.
5.
Разложить симметрический многочлен на основные симметрические 1 способом.
Разложить симметрический многочлен на основные симметрические 2 способом.
Вычислить результант.
Вычислить дискриминант.
Решить систему 2 степени от 2-х неизвестных.
Контрольная работа № 2.
Тема«Группы,кольца, поля».
1.
2.
3.
4.
Определить является ли данное множество группой (кольцом, полем).
Разложить группу по подгруппам.
Найти нормальный делитель данной группы.
Найти число элементов фактор группы данной группы.
Коллоквиум.
1. Исключение неизвестной из системы двух уравнения с двумя неизвестными.
2. Классические группы малых размерностей. Действие трупп на множествах;
3. Алгоритмы символьных преобразований (числа, многочлены, выражения,
дифференцирование, интегрирование).
Вопросы к экзаменам и зачетам по курсу «Алгебра»
Семестр 1
1. Понятие группы, примеры групп.
2. Понятие кольца , примеры колец.
3. Понятие поля, примеры полей.
4. Кольца классов вычетов.
5. Метод последовательного исключения неизвестных.
6. Теорема о ненулевых решениях однородных систем.
7. Определители второго порядка.
8. Определители третьего порядка.
9. Подстановки. Четность и знак подстановки.
10. Определение определителя произвольного порядка.
11. Свойства определителей 1-3.
12. Свойства определителей 4-6.
13. Вычисление определителей с помощью элементарных преобразований.
14. Определитель Вандермонда.
15. Миноры и алгебраические дополнения.
16. Теорема Лапласа.
17. Разложение определителя по строке и столбцу.
18. Правило Крамера.
19. Ненулевые решения квадратных однородных систем линейных уравнений.
20. Комплексные числа в алгебраической форме.
21. Геометрическое представление комплексных чисел и операций над ними.
22. Тригонометрическая форма комплексных чисел.
23. Формула Муавра.
24. Корни из комплексных чисел.
25. Многочлены деления круга.
26. Математическая индукция, бином Ньютона.
27. Вычисление сумм и произведений с помощью комплексных чисел.
28. Связь комплексных чисел с геометрией на плоскости.
Семестр 2
1. Арифметические пространства.
2. Линейная зависимость векторов.
3. Базис и ранг конечной системы векторов.
4. Элементарные преобразования матриц.
5. Вычисление ранга матрицы.
6. Критерий совместности системы линейных уравнений.
7. Равенство рангов строк и столбцов матрицы.
8. Свойства решений систем линейных однородных уравнений.
9. Фундаментальная система решений однородных систем.
10. Общее решение неоднородных систем линейных уравнений.
11. Операции над матрицами, их свойства.
12. Понятие обратной матрицы.
13. Элементарные матрицы.
14. Условия обратимости матриц.
15. Вычисление обратной матрицы с помощью элементарных преобразований.
16. Определитель произведения матриц.
17. Необходимые и достаточные условия равенства нулю определителя.
18. * Теорема о ранге матрицы.
19. Формула обратной матрицы, использующая алгебраические дополнения.
20. Записи и решение квадратных систем линейных уравнений в матричной форме.
21. Векторные пространства; примеры пространств.
22. Подпространства, линейная оболочка.
23. Базис, размерность векторного пространства и координаты векторов.
24. Изоморфизм векторных пространств.
25. Евклидовы пространства; примеры.
26. Процесс ортогонализации и ортонормированый базис.
27. Подпространство, ортогональное к данному.
28. Неравенство Коши - Буняковского и угол между векторами.
29. Неравенство треугольника и длина вектора.
Семестр 3
1. Определение линейных операторов; примеры операторов.
2. Ядро и образ линейного оператора.
3. Операции над линейными операторами .
4. Матрица линейного оператора.
5. Изменение координат вектора при переходе от одного базиса к другому.
6. Матрица оператора в различных базисах: подобие матриц.
7. Собственные вектора и значения.
8. Характеристическое уравнение.
9. Линейные операторы с простым спектром и приведение матриц к диагональному виду.
10. Операторы и числа Фибоначчи.
11. Операции над многочленами. Степень многочлена.
12. Деление на двучлен х – a и корни многочлена.
13. Схема Горнера.
14. Теорема Безу. Число корней многочлена.
15. Разложение многочленов по степеням двучлена х-а.
16. Кратные корни многочленов и их отделение.
17. Теорема о делении многочленов с остатком.
18. Алгоритм Евклида вычисления наибольшего общего делителя.
19. Разложение многочленов на неприводимые множители.
20. Алгебраическая замкнутость поля комплексных чисел.
21. Разложение многочленов на линейные множители над полем комплексных чисел.
Формулы Виета.
22. Сопряженность мнимых корней многочленов с вещественными коэффициентами и
разложение многочленов на полем действительных чисел на неприводимые множители
первой и второй степеней.
23. Уравнения третьей степени.
24. Уравнения четвертой степени.
25. Проблема локализации корней многочлена.
26. Целые и рациональные корни многочленов с рациональными коэффициентами. 27.
Критерий неприводимости Эйзенштейна.
28. Рациональные дроби; разложение на простейшие дроби.
29. Интерполяция; формула Лагранжа.
Семестр 4
1. Основная теорема о симметрических многочленах.
2. Метод неопределенных коэффициентов.
3. Симметрические многочлены и формулы Виета.
4. Связь алгебраических соотношений, корней и коэффициентов многочленов.
5. Результант.
6. Дискриминант многочлена.
7. Исключение неизвестной из системы двух уравнения с двумя неизвестными.
8. Простое алгебраическое расширение поля.
9. Освобождение от алгебраической иррациональности в знаменателе.
10. Геометрические построения циркулем и линейкой и разрешимость уравнений в
радикалах.
11. Построение правильных многоугольников.
12. Группы; определения и примеры.
13. Циклические группы.
14. *Симметрические и знакопеременные группы.
15. Изоморфизмы и гомоморфизмы групп.
16. Смежные классы и теорема Лагранжа.
17. Классические группы малых размерностей.
18. Действие трупп на множествах; теорема Бернсайда.
19. Образующие и определяющие соотношения.
20. Конечные группы поворотов сферы и правильные многогранники.
21. Представления групп.
22. Определение и примеры колец целых чисел, многочленов и вычетов.
23. Евклидовы кольца.
24. Кольцо целых гауссовых чисел.
25. Деление с остатком и алгоритм Евклида вычисления наибольшего общего делителя.
26. Разложение многочленов на неприводимые множители.
27. Кольца с неоднозначным разложением на простые множители.
7. УЧЕБНО-МЕТОДИЧЕСКОЕ
ДИСЦИПЛИНЫ (МОДУЛЯ)
И
ИНФОРМАЦИОННОЕ
ОБЕСПЕЧЕНИЕ
Основная литература
1. Курош А.Г. Курс высшей алгебры. М., Наука, 1987.
Кострикин А.И. Ведение в алгебру. М., Наука, 1998.
Куликов Л.Я. Алгебра и теория чисел. М., Высшая школа, 1989.
2. Боревич З.И., Шафаревич И.Р. Теории чисел. М., Наука, 1985.
3. Виноградов И.М. Основы теории чисел. М., Наука, 1984.
4. Нечаев В.И. Элементы криптографии. М. Высшая школа, 1999.
5. Молдовян А.А. и др. Криптография. СПб: Лань, 2000.
Дополнительная литература
6. Ван дер Варден Б.Л. Алгебра. М., Наука, 1976, 1989.
7. Дэвенпорт Г. Высшая арифметика. Наука, 1965.
8. Ленг С. Алгебра. Мир, 1978.
9. Лидл Р., Нидеррайтер Г. Конечные поля. М., Мир, 1988. М.
10. Аршинов М.Н., Садовский Л.Е. Коды и математика. М., Наука, 1991.
11. Кук Д., Бейлз Г. Компьютерная математика. М., Наука, 1990.
12. БИРКГОФ Г., БАРТИ Т. СОВРЕМЕННАЯ ПРИКЛАДНАЯ АЛГЕБРА. М., ФАКТОРИАЛ, 2000.
ГРЕХЕМ Р., КНУТ Д., ПАТАШНИК О. КОНКРЕТНАЯ МАТЕМАТИКА. М. МИР, 1998.
Дополнительная литература к практическим занятиям и самостоятельной
работе
13. Дьяконов В.П. Mathematica-4. М.: Нолидж, 2000.
14. Дьяконов В.П. MATLAB. СПб: Питер, 2001.
15. Иванов М.А. Криптография. М.: КУДИЦ-ОБРАЗ, 2001.
16. Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел. М., Просвещение, 1993.
17. Математический энциклопедический словарь, под ред. Прохорова Ю.В. М.: Сов.
энциклопедия, 1988.
18. Новиков Ф.А. Дискретная математика. СПб: Питер, 2001.
19. Проскуряков И.В. Сборник задач по линейной алгебре. М., Наука 1987.
20. Сборник задач по алгебре. Под редакцией А.И. Кострикина. М., Факториал, 1995.
21. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М., Наука, 1987.
22. Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях. Минск,
Высшая школа, 1986.
23. Ященко В.В. Введение в криптографию. СПб: Питер, 2001.
8. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ
ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
(МОДУЛЯ)
учебные аудитории для проведения лекционных и семинарских занятий
Программа составлена в соответствии с требованиями ФГОС ВПО с учетом
рекомендаций и ПрООП ВПО по направлению _____________________________и
профилю подготовки ________________________________________________________
Рабочую программу составил доцент кафедры алгебры и теории чисел Евсеева Ю.Ю.
Рецензент (ы) _________________________
Программа рассмотрена и одобрена на заседании кафедры алгебры и теории чисел
протокол № _2___от 28 сентября 2011 года.
Заведующий кафедрой доктор ф.-м. н., профессор Журавлев В. Г.
Рабочая программа рассмотрена и одобрена на заседании учебно-методической
комиссии направления_____________________________________________________________
протокол № ________от ___________ года.
Председатель комиссии_______________________________________________________
Программа переутверждена:
на_____________учебный год. Протокол заседания кафедры № ________от __________года.
Заведующий кафедрой__________________
на_____________учебный год. Протокол заседания кафедры № ________от __________года.
Заведующий кафедрой__________________