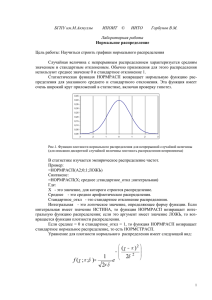
3.3. Задание 3. Нормальное распределение

1
Лабораторная работа № 1
Распределение вероятностей
1. Подготовка к работе
Изучить методику работы специализированного подключаемого модуля StatPlus
пакета Excel, ответить на контрольные вопросы.
2. Контрольные вопросы
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
Что такое случайная переменная?
Распределение вероятностей и его основные свойства.
Чем случайная переменная отличается от наблюдения?
Приведите расчетные формулы для вероятностей.
Что такое плотность вероятности?
Как сгенерировать нормально распределенные данные?
Что такое нормальная метка?
Как построить гистограмму с помощью модуля StatPlus?
Нормальное распределение и его характеристики.
3. Задания на выполнение лабораторной работы
3.1. Задание 1. Расчет вероятностей
Используя функции Excel c учетом варианта (таблица 1), определить:
1. Какова вероятность того, что при подбрасывании A монет орел выпадет B раз;
2. Значение нормального интегрального распределения для числа C;
3. Значение стандартного нормального распределения для вероятности p;
4. Вероятность случайной переменной с нормальным распределением с параметрами:
значение – x, среднее распределение - , стандартное отклонение - ;
5. Значение нормального распределения с параметрами: среднее распределение - ;
стандартное отклонение - ; вероятность – p.
Таблица 1
№ вар.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
A
10
45
12
1
6
9
11
7
70
10
7
14
13
12
B
10
>15
>3
1
0
>3
<5
1
65
0
<2
10
13 >11
C
0,5 -0,02
1,5
-0,5 1,96
3
-3 0,001 0,02 0
1,65 -1,6
1
0,2
p
0,05
0,1
0,5
0,75 0,99 0,65 0,45 0,33 0,9 0,97 0,02 0,15 0,7 0,99
x
1,96
1,9
-1,96
1,6 0,99
2
1,96 1,79 1,96 1,64 1,55 -1,7 0,6 0,99
0
1
0,2
0
0
0
2
0
1
0
0
0
0,3
0

1
0,5
0,25
1
0,2
2
0,5
0,5
1
1
0,25
0,4
1
1

3.2. Задание 2. Определение ожидаемого значения
1. Генерации нормально распределенных данных
Сгенерировать выборку случайных и нормально распределенных значений с учетом параметров
из таблицы 2.
Таблица 2
Номер вар.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Количество 100 90
80
75
85
96
102 70
109 144 120 111 97
155
наблюдений
Среднее
100 99
98
97
96
95
94
93
92
91
90
89
88
112
значение
Стандартное 19
20
21
22
23
24
25
26
27
28
29
30
31
32
отклонение
2
2. Создание диаграммы для случайных и нормально распределенных данных
После создания случайной выборки нормально распределенных данных необходимо построить
гистограмму полученного распределения.
3. Создание диаграммы вероятностей нормального распределения
4. Определение ожидаемого значения
Вычислить нормальные метки (п.3) и масштабировать их для сравнения с реальными
данными. Это можно сделать, умножая нормальные метки на стандартное отклонение
наблюдаемых значений и прибавляя наблюдаемое среднее. Результат свести в таблицу 3.
Таблица 3
Наблюдаемое значение
Нормальная метка
Ожидаемое нормально
распределенное значение
3.3. Задание 3. Нормальное распределение
Для выполнения данного задания использовать приложение 1 к лабораторной работе.
1. Создание гистограммы кривой плотности вероятности цен на дома. Удовлетворяют ли
эти данные нормальному распределению?
2. Вычислить среднюю цену и стандартное отклонение для распределения цен на дома (с
вероятностью 95%).
3. Создайте новый столбец с логарифмами цен на дома. Создайте гистограмму с кривой
нормального распределения
и кривой плотности вероятности. Удовлетворяют ли эти
логарифмированные данные нормальному распределению в большей степени, чем исходные
данные?
4. Методические указания
Для выполнения лабораторной работы необходимо загрузить подключаемый модуль
StatPlus. Кроме того, для корректного действия данного модуля нужно установить на
компьютере региональный стандарт Английский (США). Для этого в системе Windows следует
выбрать команду Пуск  Панель управления, затем в диалоговом окне Панель управления
нужно выбрать элемент Язык и региональные стандарты, после чего во вкладке Региональные
параметры диалогового окна Язык и региональные стандарты выбрать в списке элемент
Английский (США).
Выполнение лабораторной работы целесообразно начинать с изучения приведенных в
методических указаниях примеров.
4.1. Функции для расчета вероятностей
БИНОМРАСП
Синтаксис:
БИНОМРАСП(число_успехов; число_испытаний; вероятность_успеха; интегральная)
Результат:
Возвращает отдельное значение биномиального распределения.
Аргументы:
Число_успехов — это количество успешных испытаний.
Число_испытаний — это число независимых испытаний.
Вероятность_успеха — это вероятность успеха каждого испытания.
Интегральная — это логическое значение, определяющее форму функции. Если аргумент
интегральная имеет значение ИСТИНА, то функция БИНОМРАСП возвращает интегральную
функцию распределения, то есть вероятность того, что число успешных испытаний не менее
значения аргумента число_успехов; если этот аргумент имеет значение ЛОЖЬ, то возвращается
функция распределения, то есть вероятность того, что число успешных испытаний в точности
равно значению аргумента число_успехов.
НОРМСТРАСП
3
Синтаксис:
НОРМСТРАСП(z)
Результат:
Возвращает стандартное нормальное интегральное распределение.
Аргументы:
z — значение, для которого строится распределение.
НОРМСТОБР
Синтаксис:
НОРМСТОБР(вероятность)
Результат:
Возвращает обратное значение стандартного нормального распределения.
Аргументы:
Вероятность — вероятность, соответствующая нормальному распределению.
НОРМРАСП
Синтаксис:
НОРМРАСП(x; среднее; стандартное_откл; интегральная)
Результат:
Возвращает нормальную функцию распределения для указанного среднего и стандартного
отклонения.
Аргументы:
x — значение, для которого строится распределение.
Среднее — среднее арифметическое распределения.
Стандартное_откл — стандартное отклонение распределения.
Интегральная — логическое значение, определяющее форму функции. Если интегральная
имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию
распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности
распределения.
НОРМОБР
Синтаксис:
НОРМОБР(вероятность; среднее; стандартное_откл)
Результат:
Возвращает обратное нормальное распределение для указанного среднего и стандартного
отклонения.
Аргументы:
Вероятность — вероятность, соответствующая нормальному распределению.
Среднее — среднее арифметическое распределения.
Стандартное_откл — стандартное отклонение распределения.
4.2. Пример выполнения задания 2
После включения компьютера и загрузки операционной системы Widows для запуска
Microsoft Excel необходимо активизировать команду в главном меню или активизировать
соответствующую пиктограмму (ярлычок) на рабочем столе. После этого программа Excel
загрузится в оперативную память и на экране будет открыта рабочая книга. Активизировать
модуль StatPlus.
Возьмем выборку из 50 наблюдений, которые соответствуют нормальному распределению с
=100 и =15.
Для создания 50 случайный и нормально распределенных значений необходимо:
- команда меню StatPlus  Create Data  Random Numbers
- в диалоговом окне Create Random Numbers необходимо выбрать:
 в списке Type of distribution (Тип распределения) – Normal (Нормальное);
 в поле Number of samples to generate (Количество создаваемых выборок) – 1;
 в поле Size of each sample (Размер каждой выборки) – 50;
 в поле Mean (Среднее) – 100;
 в поле Standard deviation (Стандартное отклонение) – 15;
4
 на кнопке Output, в диалоговом окне Output Options выбирается переключатель Cell и
указывается ячейка А1 в качестве места назначения.
Рис. 1. Диалоговое окно Create Random Numbers
После выполнения этих действий Excel создает случайную выборку из 50 наблюдений, которые
соответствуют нормальному распределению с =100 и =15 в диапазоне ячеек А1:А50.
После создания случайной выборки нормально распределенных данных строится
гистограмму полученного распределения. Для этого:
 меню StatPlus  Single Variable Charts  Histograms;
 в диалоговом окне Create Histograms необходимо щелкнуть на кнопке Data Values, затем в
диалоговом окне Input Options выбрать переключатель Use Range References и указывается
диапазон ячеек А1:А50;
 необходимо установить флажок параметра Normal curve (Нормальная кривая);
 необходимо щелкнуть на кнопке Output, затем в диалоговом окне Output Options выберем
переключатель As a New Chart Sheet и указать имя нового листа.
Для корректного отображения исходных данных для гистограммы, необходимо перейти в
лист диаграммы, щелкнуть правой кнопкой мыши и выбрать команду Исходные данные в
контекстном меню. В диалоговом окне Исходные данные выбрать вкладку Ряд, затем указать в
поле Подписи оси Х диапазон ячеек с координатами корзин гистограммы, для Ряд 2 – указать
диапазон ячеек Normal. Для кривой нормального распределения, нужно щелкнуть правой
кнопкой мыши на столбцах Ряд 2 и выбрать команду Тип диаграммы в контекстном меню. В
диалоговом окне Тип диаграммы выберите основной тип График.
Рис. 2. Гистограмма для случайной выборки из 50 наблюдений, которые
соответствуют нормальному распределению
Для проверки степени соответствия данных нормальному распределению вычисляются
нормальные метки. Нормальная метка – это ожидаемое значение для выборки, которое
соответствует стандартному нормальному распределению.
Для создания диаграммы нормального распределения необходимо:
5
 меню StatPlus  Single Variable Charts  Normal P-plots;
 в диалоговом окне Create Normal Probability Plot необходимо щелкнуть на кнопке Data Values,
затем в диалоговом окне Input Options выбрать переключатель Use Range References указать
диапазон ячеек А1 :А50.
 щелкнуть на кнопке Output, затем в диалоговом окне Output Options выбрать переключатель As
a New Chart Sheet и указать имя нового листа диаграммы вероятностей.
На рис. 3 показана полученная в результате диаграмма вероятностей нормального распределения
Точки на диаграмме располагаются очень близко от прямой линии, что означает их близкое
соответствие нормальному распределению.
Рис. 3. Диаграмма вероятностей нормального распределения для выборки из
50 нормально распределенных наблюдений
Чтобы определить ожидаемые значения среднего нужно вычислить нормальные метки и
масштабировать их для сравнения с реальными данными. Это можно сделать, умножая
нормальные метки на стандартное отклонение наблюдаемых значений и прибавляя наблюдаемое
среднее. В примере наблюдаемое среднее для случайных данных равно 109,19, а стандартное
отклонение — 19,23. Если самая крупная нормальная метка равна 2,243, то ожидаемое среднее
будет равно 2,243*19,23+109,19 = 152,323, что немного больше наблюдаемого среднего 140,238.
Для определения нормальных меток следует установить указатель мыши над отдельной точкой
на диаграмме вероятностей нормального распределения.
Для вычисления параметров описательной статистики полученного распределения
необходимо:
 меню StatPlus  Descriptive Statistics  Univariate Statistics
 в диалоговом окне Univariate Statistics щелкнуть на кнопке Input, в появившемся диалоговом
окне Input Options выбирается переключатель Use Range References и указывается диапазон
А1:А50.
 вкладка Summary (Итоговые параметры)  флажки Count (Количество) и Average (Среднее)
 вкладка Variability (Изменчивость)  флажок Std. Deviation (Стандартное отклонение)