РОСЖЕЛДОР
реклама

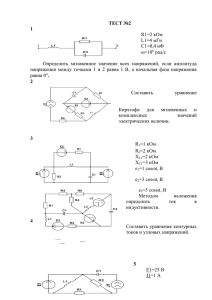
Содержание 1. Расчет переходных ht и импульсных k t характеристик первой и второй схем в соответствии с заданием_______________________________ 2. Определение откликов этих схем на воздействие заданного сигнала S t вх ______________________________________________________ Построение графиков: - исходного сигнала: S t вх; - переходных и импульсных функций первой и второй схем; - графики откликов: S t вых. 3. Определение частотных функции первой и второй схем:________ 1) комплексные коэффициенты передачи K(j ); 2) амплитудно-частотную характеристику (АЧХ); 3) фазочастотную характеристику (ФЧХ); 4) групповое время запаздывания (ГВЗ). Построение графиков АЧХ, ФЧХ и ГВЗ. 4. Вычисление импульсной характеристики, используя K(j )_____ 5. Определение А-параметров первой и второй схем_____________ 6. Составление схемы сложного 4-полюсника путём каскадного соединения схем 1 и 2 и вычисление его А- параметров__________________ 7. Получение выражения для K j , АЧХ, ФЧХ, ГВЗ при заданной нагрузке Zн, используя А-параметры сложного 4-полюсника_______________ Построение графиков АЧХ , ФЧХ, ГВЗ 8. Вычисление характеристических сопротивлений Z C1 , Z C2 и Zвх. 4-полюсника. Вычисление собственного, рабочего и вносимого затухания:__ 1) при Z вн Z c1 , Z н Z c2 ; 2) при заданных Z вн и Z н . 9. Разложение заданного сигнала тригонометрический ряд Фурье__ 10. Вычисление составляющих амплитудного и фазового спектра. Построение спектральной диаграммы.__________________________________ 11. Вычисление спектральной функции и амплитудного спектра заданного сигнала, рассматривая его как одиночный. ____________________ 12. Определение спектральным методом отклика цепи, полученной в п.6, на заданный сигнал. Построение графика амплитудного спектра отклика, включающий три полуволны.__________________________ Задание на курсовую работу. Вариант 53. Схемы: 2-/8+. Номер сигнала: 7. U m 6 В. k 2. 0,3 мс. 0 2f 0 . 3 1 мс . Z в н 0,4 кОм . Z н 2,1 j 0,8 кОм . . Схема №2 R1=15 кОм L=0,07 Гн R2=12 кОм Схема №8. R1=5 кОм L=0,04 Гн R2=1 кОм 1. Расчет переходных h(t) и импульсных k(t) характеристик цепи. а) Для схемы №2. R1=15 кОм L=0,07 Гн Z1 ( P) R2=12 кОм R1 LP ; R1 LP Z 2 ( P ) R2 ; Ku1 P Z2 R2 R1 R2 R2 LP R1 LP R1 LP R2 R1 R2 LP Z1 Z 2 R2 R1 LP Ku1 ( Р ) - операторный коэффициент передачи первой схемы. H 1 P Ku1 P , H1(P) – операторная переходная характеристика. P H 1 P R1 R2 R2 LP R1 LP R2 R1 R2 LP P Корни характеристического уравнения: P1 0 , P2 R1 R2 , P2 95238. LR2 R1 F1 P R1 R2 R2 LP , F1 ( P1 ) R1 R2 1,8 108 F1 ( P2 ) R1 R2 R2 LP 108 F2 P 2 R1 LP R2 R1 2 R2 LP . F2 P1 1,8 10 8 F2 P2 R1 2 R2 R1 PC R2 1,8 10 8 ht F1 P1 P1 t F1 P2 P2 t e e , F2 P1 F2 P2 F1 P1 1,8 10 8 1, 8 F2 P1 1,8 10 F1 P2 10 8 0,556 . 8 F2 P2 1,8 10 ht 1 0,556 e 95238t -переходная характеристика. Расчёт импульсной характеристики: K1 P Ku1 P , R1 R2 R2 LP . K 1 P R1 LP R2 R1 R2 LP R1 R2 , P1 95238 . P1 L( R1 R2 ) F1 P R1 R2 R2 LP , F ' 2 P L( R1 R2 ) . F P k t 1' 1 e P1 t , F2 P1 k t 52950 e 95238t . t Учитывая, что: ht при h0 0 k t h0 t ht при h0 0 R2 0,444 R1 R2 Окончательно получим: k (t ) 0,444 (t ) 52950 e 95238t б) Для схемы №8. R1=5 кОм L=0,04 Гн R2=1 кОм Z 2 ( P) R2 PL; Z1 ( P) R1 ; Ku1 P Z2 R2 PL Z1 Z 2 R1 R2 PL Ku1 ( Р ) - операторный коэффициент передачи первой схемы. H 1 P Ku1 P , H1(P) – операторная переходная характеристика. P H 1 P R2 PL R1 R2 PLP Корни характеристического уравнения: P1 0 , P2 R1 R2 , L P2 150000 F1 P R2 PL F1 P1 R2 PL 1000 F1 P2 R2 PL 5000 F2 P R1 R2 2 PL . F2 P1 R1 R2 2 PL 6000 F2 P2 R1 R2 2 PL 6000 ht F1 P1 P1 t F1 P2 P2 t e e , F2 P1 F2 P2 F1 P1 1000 0,167 , 6000 F2 P1 F1 P2 5000 0,833 . 6000 F2 P2 ht 0,167 0,833e 150000t -переходная характеристика. Расчёт импульсной характеристики: R2 jL R2 PL R1 1 R1 R2 jL R1 R2 PL R1 R2 PL R R2 , P1 1 P1 150000 L F2/ P L 0,04 . F1 P R1 5000 ; K P k t F1 P1 P1 t e ; k 2 (t ) (t ) 125000 e 150000t . F2 P1 2. Определение откликов первой и второй схем на воздействие заданного сигнала методом интеграла Дюамеля. Um t , если 0 t S (t ) 0, если t ht d S t вых S 0вх ht S вх t 0 Для схемы №2: ht 1 0,556 e 95238t U вых1 (t ) Um Um t h(t ) d 0 t 5,838 10 6 Um t 95238( t ) d 1 0,556 e 0 5,838 10 6 е 95238t Um 5,838 10 6 е 95238( t ) t 0 В интервале времени t : U вых2 (t ) Um Um h(t ) d S h(t ) 0 5,838 10 6 Um 5,838 10 6 е 95238( t ) е 95238( t ) 5,838 10 6 е 95238t S h(t ) 0 S h(t ) Отклик схемы №2. Для схемы №8: ht 0,167 0,833e 150000t U вых1 (t ) Um Um t h(t ) d 0 0,167t 5,55 10 6 Um t 0,167 0,833 e 150000( t ) d Um 0 5,55 10 6 е 150000t 0,167 5,55 10 6 е 150000(t ) В интервале времени t : U вых2 (t ) Um Um h(t ) d S h(t ) 0 0,167 5,55 10 6 Um 0,167 5,55 10 6 е 150000(t ) е 150000(t ) 5,55 10 6 е 150000t S h(t ) Отклик схемы №5. 0 S h(t ) t 0 3. Определение частотных функций цепей а). Комплексный коэффициент передачи по напряжению: K j U в ых ; U в х K j A jB , где A ReK j ; B JmK j ; в показательной форме K j K ( j ) j . б). Модуль комплексного коэффициента передачи АЧХ: K j A B . 2 2 в). Аргумент комплексного коэффициента передачи ФЧХ: arctg B (берется главное значение угла). A 4. Групповое время запаздывания ГВЗ: ГВЗ 0 d d . Для схемы №2. Z1 ( P) jR1 L ; R1 jL Z 2 ( P ) R2 ; Z2 R2 R1 jL R22 R12 2 R2 L2 ( R1 R2 ) K1 j Z1 Z 2 R1 R2 jLR2 R1 R12 R22 2 L2 ( R1 R2 ) 2 j R22 LR1 LR1 R2 ( R1 R2 ) R12 R22 2 L2 ( R1 R2 ) 2 A( ) R22 R12 2 R2 L2 ( R1 R2 ) R12 R22 2 L2 ( R1 R2 ) 2 B( ) R22 LR1 LR1 R2 ( R1 R2 ) R12 R22 2 L2 ( R1 R2 ) 2 K j A B R2 2 2 R12 2 L2 - (АЧХ). R12 R22 2 L2 ( R1 R2 ) 2 LR12 B - (ФЧХ). arctg arctg 2 2 2 A R R L ( R R ) 1 2 2 1 LR12 2 L2 ( R1 R2 ) R12 R2 d ГВЗ 0 2 d R1 2 L2 R12 R22 2 L2 ( R1 R2 ) 2 Для схемы №8. Z 1 R1 ; Z 2 R2 jL; K 1 j Z2 R2 jL ( R jL)( R1 R2 jL) R2 ( R1 R2 ) 2 L2 2 Z1 Z 2 R1 R2 jL ( R1 R2 ) 2 2 L2 ( R1 R2 ) 2 2 L2 jLR1 ( R1 R2 ) 2 2 L2 R2 ( R1 R2 ) 2 L2 A( ) ( R1 R2 ) 2 2 L2 B( ) LR2 ( R1 R2 ) 2 2 L2 K j - (АЧХ). A B 2 2 R1 R2 2 R2 R1 2 R1 R2 2 L2 R2 3 2 L2 R2 4 L4 2 2 3 4 ( R1 R2 ) 2 2 L2 2 arctg LR2 B arctg 2 2 A R2 ( R1 R2 ) L LR2 ( R2 ( R1 R2 ) 2 L2 ) 2L2 LR2 2 ( R2 ( R1 R2 ) 2 L2 ) 2 LR2 1 2 2 R2 ( R1 R2 ) L LR2 ( R2 ( R1 R2 ) 2 L2 ) 2L2 LR2 d ГВЗ 0 d - (ФЧХ). R ( R 2 1 R2 ) 2 L2 1 2 2 L2 R22 4. Связь между импульсной и частотной функциями цепи Связь между импульсной k(t) и частотной K(jω) функциями цепи устанавливается следующим образом: K j k t e jt dt; o 1 k t 2 K j e jt dt , т. е. K(jω) и k(t) связаны между собой соотношениями прямого и обратного преобразований Фурье. Для схемы №2. K1 j Z2 R2 R1 jL Z1 Z 2 R1 R2 jLR2 R1 Заменим K1 j P1 j на P : Z2 R2 R1 PL Z1 Z 2 R1 R2 PLR2 R1 R1 R2 , P1 95238. LR1 R2 F1 P R2 R1 PL 100000080 ; R2 0,444 R1 R2 k (t ) 0,444 (t ) 52950 e 95238t . F2/ P LR2 R1 1890 . Импульсная характеристика, полученная в данном пункте, сошлась с импульсной характеристикой, получившейся в пункте №1. Для схемы №8. K 2 j Заменим Z2 R2 jL Z1 Z 2 R1 R2 jL j на P : R2 jL R2 PL R1 1 R1 R2 jL R1 R2 PL R1 R2 PL R R2 , P1 1 P1 150000 L F2/ P L 0,04 . F1 P R1 5000 ; K P k t F1 P1 P1 t e ; k 2 (t ) (t ) 125000 e 150000t . F2 P1 Импульсная характеристика, полученная в данном пункте, сошлась с импульсной характеристикой, получившейся в пункте №1. 5. Определение А-параметров первой и второй схем. Для схемы №2. R1=15 кОм L=0,07 Гн R2=12 кОм Схема замещения. Z1 jR1 L R1 jL Z 2 R2 A1 _ 11 1 A1 _ 11 1 Z1 ( ) ; Z 2 jR1 L jL( R1 R2 ) R1 R2 ; R1 jLR2 R1 jLR2 A1 _ 12 Z 1 , A1 _ 12 jR1 L , R1 jL A1 _ 21 A1 _ 21 1 , R2 1 Z 2 , Матрица А схемы №2: jL( R1 R2 ) R1 R2 R1 jL R2 A 1 R2 jR1 L R1 jL . 1 А1 _ 22 1 . Для схемы №8. R1=5 кОм L=0,04 Гн R2=1 кОм Схема замещения. Z 2 R2 jL Z1 R1 A1 _ 11 1 A1 _ 11 1 Z1 Z 2 ; R1 R jL R1 ; 2 R2 jL R2 jL A1 _ 12 Z 1 , A1 _ 12 R1 , A1 _ 21 A1 _ 21 1 Z 2 , Матрица А схемы №8: R2 R2 A R 2 jL R1 jL 1 jL R1 . 1 1 , R 2 j L А1 _ 22 1 . 6. Составление схемы сложного 4-полюсника путём каскадного соединения схем 1 и 2 и вычисление его А – параметров. A A12 A 11 , A21 A22 A A1_12 A2_11 A2_12 A 1_11 A1_ 21 A1_ 22 A2_ 21 A2_ 22 R1=15 кОм R3=5 кОм L1=0,07 Гн L2=0,04 Гн R2=12 кОм R4=1 кОм A11 A1_11 A2_11 A1_12 A2_21 jL1 ( R1 R2 ) R1 R2 R1 jL1 R2 A1 1 R2 R4 jL2 R3 R4 jL2 A2 1 R jL 4 2 jR1 L1 R1 jL1 1 R3 1 jL1 ( R1 R2 ) R1 R2 R4 jL2 R3 jR1 L1 1 A11 ( ) R1 jL1 R2 R4 jL2 R1 jL1 R4 jL2 7,5 1010 3 2 j 1,45 10 6 0,75 j 2,5 10 4 3,75 10 5 j A12 A1 _ 11 A2 _ 12 A1 _ 12 A2 _ 22 jL1 ( R1 R2 ) R1 R2 jR1 L1 j 7 5 10 5 A12 ( ) R 3750 R1 jL1 R2 3 R1 jL1 3,75 10 5 j A21 A1 _ 21 A2 _ 11 A1 _ 22 A2 _ 21 A21 ( ) 1 R2 R4 jL2 R3 5 j 1,1 10 5 1 7,5 4 2,5 10 j R4 jL2 R4 jL2 A22 A1_21 A2_12 A1_22 A2_22 A22 ( ) R3 17 1 R2 12 7. Вычисление частотных функций сложного 4-полюсника Комплексный коэффициент передачи K j выражается через Апараметры следующим образом: K j Zн . A11 Z н А12 Неравномерность АЧХ в полосе пропускания н в определяется как разность K j max K j min K , при этом K может быть выражено в разах или в дБ (20lg ∆ k/). Условие неискаженной передачи сигналов формулируется следующим образом: для неискаженной передачи сигнала с полосой, ограниченной в интервале н в , модуль комплексного коэффициента передачи 4-полюсника K j в заданном интервале не должен зависеть от частоты и равен некоторой постоянной величине K 0 ; ФЧХ должна изменяться пропорционально частоте t 0 ; ГВЗ должно быть постоянным K j 2100 j800 7,5 10 3 j 1,45 10 6 j 7 5 10 5 0,75 2100 j 800 3750 j 2,5 10 4 3,75 10 5 j 3,75 10 5 j 10 2 113 2 7,03 1010 K j 18 2 3 7,42 105 2 8 109 1,6 1015 Амплитудно-частотная характеристика ωн=10 Гц ωв=120000 Гц K =0,06 arctg B A Фазо-частотная характеристика. ГВЗ 0 d d Групповое время запаздывания. 8. Вычисление характеристических и входного сопротивлений. Характеристические сопротивления 4-полюсника зависят от его параметров и определяются следующим образом: Z c1 A11 A12 ; A21 A22 A22 A12 ; A21 A11 Z c2 Z вх A11 Z н А12 . А21 Z н А22 Здесь Z c1 - характеристическое сопротивление со стороны входа; Z c2 - характеристическое сопротивление со стороны выхода. Расчет ведем для 0 10472 Гц. 7,5 1010 3 2 j 1,45 10 6 3750 j 7 5 10 5 0,75 j 2,5 10 4 3,75 10 5 j 3,75 10 5 j 3771,6 j506,7 Ом Z c1 5 j 1,1 10 5 17 7,5 2,5 10 4 j 12 Z c2 17 j 7 5 10 5 3750 12 3,75 10 5 j 5 j 1,1 10 5 7,5 2,5 10 4 j Z вх 7,5 1010 3 2 j 1,45 10 6 0,75 j 2,5 10 4 3,75 10 5 j 2100 j800 0,75 7,5 10 17 2,5 10 j 12 2100 j800 7,5 5 j 14,110 5 Собственные параметры 4-полюсника Постоянная передачи: 898,5 j 335,7 Ом 3750 j 7 5 10 3,75 10 j 3908,84 j 473,47 Ом 3 2 j 1,45 10 6 j 2,5 10 4 3,75 10 5 j 10 5 5 g a jb , где a - собственная постоянная затухания 4-полюсника, b - собственная постоянная фазы. g ln g ln A11 A22 A12 A21 , 7,5 1010 3 2 j 1,45 10 6 0,75 j 2,5 10 4 3,75 10 5 j j 7 5 10 5 3750 3,75 10 5 j 7,5 5 j 1,1 10 2,5 10 j 17 5 4 12 3,66 j 0,45 Рабочее затухание 4-полюсника aр a ln где Pвн Z вн Z c1 2 Z вн Z c1 Z н Z c2 ln 2 Z н Z c2 ln 1 Pвн Pн e 2 g , Z вн Z c1 Z Z c2 ; Pн н - коэффициенты несогласованности на Z н Z c2 Z вн Z c1 входе и выходе 4-полюсника соответственно. Вносимое затухание 4-полюсника aв a ln Z вн Z c1 2 Z вн Z c1 ln Z н Z c2 2 Z н Z c2 ln 1 Pвн Pн e 2 g ln Z вн Z н 2 Z вн Z н . 1. Вычисление затуханий при Z вн Z c1 , Ом; Z н Z c2 , Ом. При согласованной нагрузке коэффициенты несогласованности соответственно равны: Pв н Z в н Z c1 , Z в н Z c1 Pвн 0 , Pн Z н Z c2 , Z н Z c2 Pн 0 , рабочее затухание а p а ln Z вн Z c1 2 Z вн Z c1 ln Z н Z c2 2 Z н Z c2 ln 1 Pвн Pн e 2 g , Неп; а р 3,66 ln 3771,6 j506,7 3771,6 j506,7 898,5 j335,7 898,5 j335,7 ln 2 3771,6 j506,7 2 898,5 j335,7 ln 1 3,66 Неп вносимое затухание а ВН а p ln Zвн Z н 2 Z в нZ н а ВН 3,66 ln , Неп. 3771,6 j506,7 898,5 j335,7 2 3771,6 j506,7 898,5 j335,7 3,445 Неп Вычисление затуханий при заданных Z вн и Z н . Pв н Z ВН Z c1 Z в н Z c1 , Pн Zн Zc 2 Zн Zc 2 , Рвн Pн 400 3771,6 j506,7 0,955 j 0,011 400 3771,6 j506,7 2100 j800 898,5 j335,7 0,213 j 0,28 2100 j800 898,5 j 335,7 рабочее затухание а p а ln а p 3,66 ln Z вн Z c1 2 Z вн Z c1 ln Z н Z c2 2 Z н Z c2 400 3771,6 j 506,7 2 400 3771,6 j 506,7 ln 1 Pвн Pн e 2 g , Неп; ln 2100 j800 898,5 j 335,7 2 2100 j800 898,5 j 335,7 ln 1 0,955 j 0,0110,213 j 0,28e 2 3, 66 j 0, 45 6,058 Неп вносимое затухание авн а p ln Z вн Z н 2 Z вн Z н авн 6,058 ln , Неп. 400 2100 j800 2 400 2100 j800 5,309 Неп. 9. Представление периодического сигнала в виде в виде тригонометрического ряда Фурье Представление периодического сигнала S t тригонометрического ряда Фурье имеет вид: S t C 0 2 C n cosnt n , n 1 2 ; T - период повторения сигнала; T 2 T где T 1 2 C0 S t dt - величина постоянной составляющей сигнала; T T 2 1 Cn T T 2 S t e jn1t dt - амплитуды соответствующих n гармонических T 2 составляющих сигнала. 1T 1T 1T jnt C S (t )e dt S (t ) cos( nt )dt S (t ) sin( nt )dt n T T0 T0 0 Вычислим коэффициенты ряда: 1 U 1 Um 2 C0 m tdt t T 0 T 4 0 1 Um 2 1,5 , 4 U jnt t 1T U jnt 1 jnt C S (t )e dt te dt e 2 2 n T 3 0 jn n 3 0 U 2 jn 2 1 U e 2 2 2 2 2 2 2 jn n 2 4 n 0 Запишем тригонометрический ряд Фурье в виде: S t 1,5 2 n U 2 jn 2 1 e 2 2 2 2 jn n U 2 2 2 2 cosnt n 4 n 10. Вычисление амплитудного и фазового спектра периодического сигнала Амплитудным спектром периодического сигнала является множество модулей комплексных коэффициентов C n . Фазовым спектром периодического сигнала является множество аргументов комплексных коэффициентов C n . Спектральной диаграммой называется графическое изображение амплитудного или фазового спектра. В качестве спектральных составляющих будем брать коэффициенты тригонометрического ряда Фурье, где модуль C n удваивается. Отметим, что коэффициенты C n существуют только в точках, кратных n , n 0,1 и т. д. 11. Вычисление спектральной функции одиночного сигнала Спектральной функцией одиночного сигнала S t является функция S j , полученная путем выполнения над сигналом операции прямого преобразования Фурье. S ( j ) S t e jt dt . S j 0 U te jt dt Эффективная ширина спектра э в н определяется как интервал частот, в котором заключено не менее 90% энергии сигнала.В соответствии с теоремой Релея полная энергия сигнала Э выражается через спектральную функцию сигнала следующим соотношением: Э 1 S j 2 d 244,4 10 . Соответственно 0,9 Э= 6 0 следовательно, в 1 в S j 2 d , 0 2 0,9 S j d S j d 220 10 6 2 0 0 12. Спектральный (частотный) метод анализа Этот метод позволяет определить спектральную функцию отклика линейной цепи S j вых , заданной комплексным коэффициентом передачи K j при известной спектральной функции входного сигнала S j вх : S jwвх S jwвых K(jw) S j вых S j вх K j . 1. Вычислим S j вх : S j вх 0 U te jt dt . 2. Вычислим частотную функцию цепи: 113 2 7,03 1010 K j 18 2 3 7,42 105 2 8 109 1,6 1015 3. Вычислим S j вых : S j вых K j S j вх