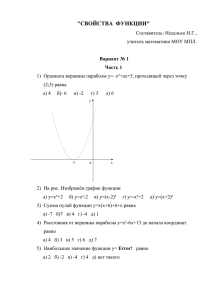
Исследуем функцию, заданную формулой: Область
реклама

3 Исследуем функцию, заданную формулой: y(x)=3x -x+2 Область определения: множество всех действительных чисел 2 Первая производная: y'(x)=9x -1 ' 3' ' 3 ' 3' ' 3' ' 3' 3x -x+2 =3x -x +(2) =3x -x +0 =3x -x =3x -1 = 2 2 2 2 =33x -1 =3·3x -1 =(3·3)x -1 =9x -1 Вторая производная: y''(x)=18x Вторая производная это производная от первой производной. ' 2' 2 ' 2' 2' 9x -1 =9x -(1) =9x -0 =9x =9(2x) =9·2x =(9·2)x =18x Точки пересечения с осью x : x=-1 Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю. 3 3x -x+2=0 3 2 2 3x +3x -3x -3x+2x+2=0 2 2 3 3x +3x -3x +3x+(2x+2)=0 (x+1)3x -(x+1)(3x)+(x+1)2=0 2 (x+1)3x -3x+2=0 2 решение исходного уравнения разбивается на отдельные случаи. Случай 1 . x+1=0 x=-1 Случай 2 . 2 3x -3x+2=0 2 2 D=b -4ac=(-3) -4·3·2=-15 Дискриминант отрицателен, значит уравнение не имеет корней. ответ этого случая: нет решений. Ответ: x=-1 . Точки пересечения с осью y : y=2 Пусть x=0 3 y(0)=3·0 -0+2=2 y(x) стремится к бесконечности при x стремящемся к бесконечности. Error! стремится к бесконечности при Error! стремящемся к бесконечности. Критические точки: Error! Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение. 2 9x -1=0 2 9x =1 2 x =1:9 Error! Ответ: Error!. Возможные точки перегиба: x=0 Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение. 18x=0 x=0:18 x=0 Точки разрыва: нет Симметрия относительно оси ординат: нет Функция f(x) называется четной, если f(-x)=f(x). y(x)-y(-x) = 3 3 3 3 =3x -x+2-3(-x) -(-x)+2 =3x -x+2-3(-x) -x-2 = 3 3 3 3 3 3 =3x -x+2+3x -x-2 =3x -x+2-2+3x -x =3x -x+0+3x -x = 3 3 3 3 =3x -x+3x -x =6x +(-2)x =6x -2x 3 6x -2x≠0 y(-x)≠y(x) Симметрия относительно начала координат: нет Функция f(x) называется нечетной, если f(-x)=-f(x). y(x)+y(-x) = 3 3 3 3 =3x -x+2+3(-x) -(-x)+2 =3x -x+2+3(-x) +x+2 = 3 3 3 3 3 3 =3x -x+2-3x +x+2 =3x -x+2+2-3x +x =3x -x+4-3x +x = 3 3 =3x -x+4-3x +x =4 4≠0 y(-x)≠-y(x) Тестовые интервалы: x<-1 y(x) - y'(x) + y''(x) - x=-1 Error! 0 + + + - Error! Error! 0 - Error! x=0 + 2 - 0 характер графика возрастает,выпукла вверх возрастает,выпукла вверх относительный максимум убывает,выпукла вверх точка перегиба Error! Error! + Error! 0 + + Error! + + + убывает,выпукла вниз относительный минимум возрастает,выпукла вниз Относительные экстремумы: Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум Error!. Проходя через точку максимума. производная функции меняет знак с (+) на (-). Относительный максимум Error!. Множество значений функции: множество всех действительных чисел Наименьшее значение: нет Наибольшее значение: нет