dz-1523bb74049b91
реклама

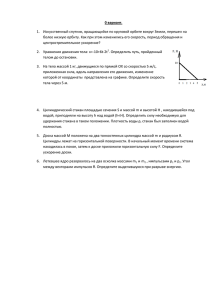
Пакет № 1 Гидро- и аэростатика, кинематика, динамика. Задача №1 В двух сосудах налиты одинаковые объемы различных жидкостей. Если пластмассовый брусок поместить в первый сосуд, то он плавает в нем, причем сторона бруска, имеющая длину а, перпендикулярна поверхности жидкости, а высота выступающей части равна h1. Если этот брусок поместить во второй сосуд, то высота выступающей части станет h2. Какой будет высота выступающей части, если обе жидкости слить в один сосуд? Считать, что жидкости смешиваются без изменения объема. Задача №2 В цилиндрическом стакане с водой плавает льдинка, притянутая ко дну ниткой (рис). Когда льдинка растаяла, уровень воды в стакане понизился на Δh. Каково было натяжение нити? Площадь дна стакана S. Задача №3 В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько изменится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3. Задача №4 В цилиндрический сосуд с водой налили V = 0,2 л масла, которое образовало на воде слой толщиной d = 1 см. Затем в сосуд опустили плоскую таблетку из сала массой m = 360 г и толщиной h = 5 см. На какую высоту L таблетка будет выступать над маслом? Плотности воды ρв= 1 г/см3, масла ρм = 0,8 г/см3, сала ρс= 0,72 г/см3. Задача №5 Гидравлический пресс с двумя поршнями разного диаметра закреплен на бетонном полу в цехе. К штокам поршней прижаты два одинаковых ящика. Минимальная сила, Рис. 1 Рис. 2 которую нужно приложить к левому ящику, чтобы сдвинуть оба ящика вправо, составляет F1 (рис. 1). Аналогично, к правому ящику необходимо приложить силу не меньше F 2, чтобы сдвинуть оба ящика влево. Какую минимальную силу F необходимо приложить к точно такому же отдельно стоящему ящику (рис. 2), чтобы сдвинуть его с места? Учитывайте трение только между ящиками и полом. Задача №6 По прямой начинает двигаться материальная точка с постоянным ускорением. Спустя время Т после начала движения ускорение точки меняет знак на противоположный, оставаясь неизменным по модулю. Определить, через какое время t после начала движения точка вернется в исходное состояние Задача №7 Во сколько раз средняя скорость автомобиля, начинающего двигаться равноускоренно, на второй половине пути больше его средней скорости на первой половине дистанции? Задача №8 Капля дождя, падающая с крыши школьного здания вертикально, пролетает мимо окна высотой h = 3 м за время t = 0,4 с. Чему равно значение ее скорости при пролете мимо нижнего и верхнего краев окна. Сопротивлением воздуха пренебречь. Ускорение свободного падения g ≈ 10 м/с2. Задача №9 На тележке, равномерно двигающейся по горизонтальной поверхности, установлена труба. Как должна быть ориентирована эта труба, чтобы капли дождя, падающие вертикально, пролетали через нее, не задевая внутренних стенок? Движение капель считать равномерным. Задача №10 Небольшая лампочка освещает вертикальную стену. Проходящий вдоль стены хулиган швырнул в лампочку камень под углом 450 к горизонту и попал в нее. Определите минимальное и максимальное значение скорости тени от камня на вертикальной стене. В момент броска камень находился на одной высоте с лампочкой на расстоянии L от нее. Задача №11 Из одной точки одновременно бросают два тела, одно – вертикально вверх, а другое – под углом 300 к горизонту. На каком расстоянии будут находиться тела через время t, если их начальные скорости одинаковы и равны v0? Задача №12 Тело влетает в некоторую вязкую среду, имеющую переменную плотность. Зависимость скорости движения от времени в данной среде показана на графике. Определите ускорение тела на 2-ой секунде движения и путь, пройденный телом в среде до полной остановки. Задача №13 Тонкая массивная шайба надета на длинный стержень радиуса R (см. рис.). Когда шайбу закрутили вокруг стержня с угловой скоростью ω, оказалось, что она останавливается через время t0. В другой раз шайбу закрутили с той же угловой скоростью и одновременно придали ей скорость V0 вдоль стержня. Какой путь пройдет по стержню шайба до остановки? Зазора между шайбой и стержнем нет. Задача №14 Тело на пружине, один конец которой закреплен на оси, двигается по окружности. При угловой скорости движения 1 длина пружины l1 , а при угловой скорости 2 - l2. Какую длину имеет пружина в нерастянутом состоянии? Задача №15 На краю доски длины L лежит резиновая пробка. Коэффициент трения покоя между резиной и доской равен μ1, коэффициент трения скольжения равен μ2. Доску медленно наклоняют, и в некоторый момент пробка начинает соскальзывать. После начала движения пробки угол между доской и горизонтом не изменяется. За какое время пробка достигнет другого края доски. Задача №16 Плот массой т = 200 кг оттолкнули от берега озера, сообщив ему начальную скорость V0 = 1 м/с. На каком расстоянии от берега остановится плот? Сила сопротивления движению плота пропорциональна его скорости: F = kv, где k = 25 кг/с. Задача №17 При скоростном спуске лыжник скользит вниз по склону (φ = 450), не отталкиваясь палками. Коэффициент трения лыж о снег μ=0,l. Сила сопротивления воздуха пропорциональна квадрату скорости лыжника Fc = αv2, где α - постоянная величина, равная 0,7 H/(м/с)2. Какую максимальную скорость может развить лыжник, если его масса 70 кг? Задача №18 В боковой стенке сосуда имеется отверстие, нижний край которого находится на высоте h. При каком горизонтальном ускорении сосуда а, налитая в него жидкость не будет выливаться из отверстия, если в неподвижном сосуде ( при закрытом отверстии) жидкость была налита до высоты Н? Задача №19 Плотно закрытый железнодорожный вагон, удаляется с постоянной скоростью V. Привязанный к его полу воздушный шарик неподвижен, а удерживающая его нить отклонена в перпендикулярном скорости направлении и составляет угол α с вертикалью (см. рис.). железнодорожный В путь? какую сторону Чему поворачивает равен радиус закругления? Задача №20 Стержень длиной 1 м лежит на земле. Один конец стержня начинают поднимать с постоянной скоростью 1,2 м/с вертикально вверх. С какой скоростью будет скользить по земле нижний конец стержня в тот момент, когда верхний окажется на высоте 80 см? Задача №21 Гладкий клин массой m и с углом наклона φ удерживают на горизонтальной плоскости. На клин опирается стержень массой М, который может свободно перемещаться в муфте В. С каким ускорением начнет двигаться клин, если его освободить? Предположим, что массы клина и груза равны. При каком угле φmax ускорение клина будет максимальным? Задача №22 Длинный шест АВ заталкивают нa крышу сарая, двигая его нижний конец А горизонтально по земле с постоянной скоростью V0 (см. рис.). Найдите скорость точек С и В шеста, когда середина стержня (точка С) попадает на край сарая. Длина шеста L, высота сарая – h. Задача №23 На кубе массой М закреплен легкий блок, через который перекинута невесомая нить. Один конец нити прикреплен к стене, а другой – к грузу массой m. С каким ускорением будет двигаться куб, если его отпустить. Трением пренебречь. Задача №24 На гладкой горизонтальной поверхности покоится уголок массой М, который при помощи легкой нити и двух блоков соединен со стенкой и бруском массой m. Брусок касается внутренней поверхности уголка. Нити, перекинутые через блок, натянуты горизонтально. Вначале систему удерживают в состоянии покоя, а потом отпускают. Найдите ускорение уголка. Трение в системе отсутствует.