Ход урока Вид доски на начало урока Этап Деятельность учителя

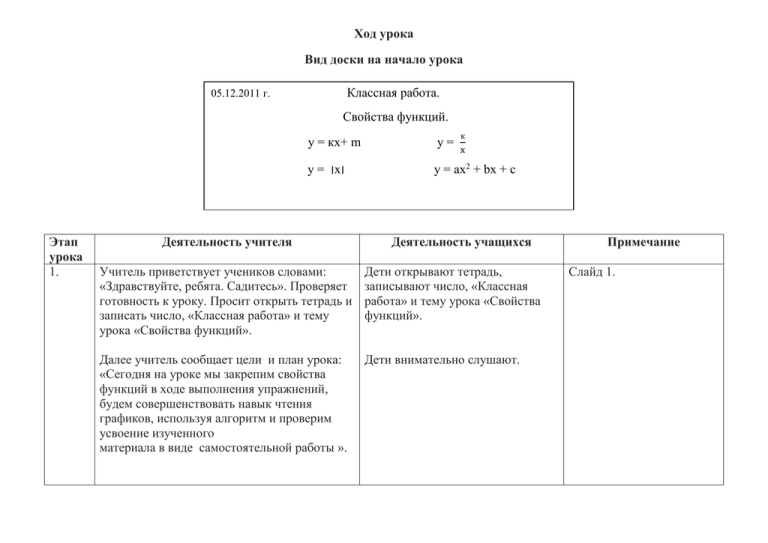
Ход урока
Вид доски на начало урока
Классная работа.
05.12.2011 г.
Свойства функций.
Этап
урока
1.
к
у = кх+ m
у=
у = ‫׀‬х‫׀‬
у = ах2 + bх + с
Деятельность учителя
x
Деятельность учащихся
Учитель приветствует учеников словами:
«Здравствуйте, ребята. Садитесь». Проверяет
готовность к уроку. Просит открыть тетрадь и
записать число, «Классная работа» и тему
урока «Свойства функций».
Дети открывают тетрадь,
записывают число, «Классная
работа» и тему урока «Свойства
функций».
Далее учитель сообщает цели и план урока:
«Сегодня на уроке мы закрепим свойства
функций в ходе выполнения упражнений,
будем совершенствовать навык чтения
графиков, используя алгоритм и проверим
усвоение изученного
материала в виде самостоятельной работы ».
Дети внимательно слушают.
Примечание
Слайд 1.
2.
1) Повторение всех свойств функций.
Ребята, в начале урока предлагаю вам
вспомнить свойства функций, которые мы
изучали на предыдущем уроке.
Учащиеся перечисляют свойства Развитие устной
функций: область определения математической речи.
функции, монотонность функции
(возрастание
или
убывание
функции),
ограниченность
функции (сверху или снизу),
наименьшее
и
наибольшее
значение функции, непрерывность
функции,
область
значений
функции, свойство
выпуклости
функции (вверх или вниз).
2) Учитель обращается к учащимся: « На
доске вы видите знакомые вам функции. На
прошлом уроке мы строили графики этих
функций и записывали их свойства. Давайте
еще раз повторим свойства данных функций.
у = кх+ m – прямая.
1) D (у) = (-∞;+∞);
2) возрастает, если к > 0, убывает,
если к < 0;
3) не ограничена;
4) нет наибольшего и наименьшего
значения;
5) функция непрерывна;
6) E (у) = (-∞;+∞).
к
у = - гипербола
𝐱
1) D (y) = (-∞; 0) U (0; +∞);
2) если k > 0, то функция убывает
на открытом луче (-∞; 0) и нам
открытом луче (0; +∞), если k < 0,
то функция возрастает на (-∞; 0) и
на (0; +∞);
3) не ограничена;
4) нет ни наименьшего, ни
наибольшего значения;
5)
функция
непрерывна
открытом луче (-∞; 0) и
открытом луче (0; +∞);
6) Е (у) = (-∞; 0) U (0; +∞);
на
на
у = ‫׀‬х‫ – ׀‬объединение двух лучей:
у = х, х ≥ 0 и у = -х, х ≤ 0
1) D (y) = (-∞;+∞);
2) убывает на луче (-∞; 0],
возрастает на луче [0; +∞);
3) ограничена снизу;
4) унаим. = 0, унаиб. не существует;
5) непрерывна;
6) Е (у) = [0; +∞).
у = ах2 + bх + с - парабола
Для случая а > 0:
1) D (y) = (-∞;+∞);
2) убывает на луче (-∞; 𝑏
𝑏
2𝑎
],
возрастает на луче [- ; +∞);
2𝑎
3) ограничена снизу;
4) унаим. = у0, унаиб. не существует;
5) непрерывна;
6) Е (у) = [у0; +∞);
7) выпукла вниз.
Для случая а < 0:
1) D (y) = (-∞;+∞);
2) возрастает на луче (-∞; 𝑏
𝑏
2𝑎
],
убывает на луче [- ; +∞);
2𝑎
3) ограничена сверху;
4) унаим. не существует, унаиб = у0;
5) непрерывна;
6) Е (у) = (-∞ ; у0];
7) выпукла вверх.
3.
3) Разминка.
Учитель предлагает ребятам устно ответить
на вопросы разминки и обращает внимание
ребят на интерактивную доску. Учитель по
очереди показывает слайды и просит назвать
неверное утверждение.
Внимательно
рассматривают Слайды 2-5.
изображенные графики функций и
ищут верный ответ. Если ответ
неверный, то предлагается еще
подумать.
Решение упражнений
Ребята, сейчас мы с вами будем упражняться
в построении графиков функций и их
прочтении.
Выполняем упражнения из учебника.
1) Постройте и прочитайте график функции:
№ 10.14.
а) у = х2 – 6х + 3;
б) у = -5х + 2
№ 10.15.(в)
в) у = ‫׀‬х‫ ׀‬+ 4
Ребята по вызову учителя выходят Формирование навыков
к доске и решают по одному
построения графиков.
заданию. Остальные решают в
Самоконтроль.
тетради, сравнивают ответы с
доской.
№ 10.14.
а) у = х2 – 6х + 3
2) Найти наибольшее и наименьшее значение
функции.
№10.20. (а)
у = - 4 х2 – 12х + 1
Во время выполнения заданий учитель
индивидуально работает с теми учащимися, у
которых возникли затруднения при решении.
Фронтальная проверка.
Индивидуальная работа с
учащимися.
1)D (y) = (-∞; +∞);
2)убывает на луче (-∞; 3],
возрастает на луче [3; +∞);
3)ограничена снизу;
4)унаим. = -6; унаиб. не существует;
5)непрерывна;
6)Е (у) = [-6; +∞);
7)выпукла вниз.
б) у = -5х + 2
D (y) = (-∞; +∞);
убывает;
не ограничена;
нет наибольшего и
наименьшего значений;
5) непрерывна;
6) Е (y) = (-∞; +∞);
7) о выпуклости говорить нет
смысла.
1)
2)
3)
4)
№ 10.15.(в)
в) у = ‫׀‬х‫ ׀‬+ 4
1)D (y) = (-∞; +∞);
2)возрастает на луче [0; +∞),
убывает на луче (-∞; 0];
3)ограничена снизу;
4)унаиб. не существует, унаим. = 4;
5)непрерывна;
6)Е (y) = [4; +∞);
7)выпукла вниз.
№10.20. (а)
у = - 4 х2 – 12х + 1
у = -4х2 – 12х + 1 – квадратичная
функция, ее график – парабола,
ветви которой направлены вниз.
𝑏
12
3
Хb = - ; Хb =
= - ; уb = 9
2𝑎
3
−8
2
4* + 12* + 1 = -9 + 18 + 1 = 10
4
2
Унаиб. = 10; унаим. не существует.
Самостоятельная работа по вариантам.
1) Постройте и прочитайте график функции.
№10.15.(б, г)
1 вариант
5
б) у = + 2;
x
2 вариант
−3
г) у = ;
x
2) Найдите наибольшее и наименьшее
значение функции.
№10.21.(б,в)
1 вариант
б) у = -3х2 + 6х + 2;
2 вариант
в) у = - ‫׀‬х‫׀‬
3) Дополнительное творческое задание.
После выполнения обязательной части
самостоятельной работы предлагаю вам
выполнить творческое задание на
дополнительную оценку.
Задание: придумайте свою функцию,
запишите её, постройте график этой функции
и опишите её свойства.
Выполняют самостоятельно в
тетради и сдают на проверку.
№10.15.(б, г):
5
б) у = + 2
x
1)D (y) = (-∞;0) U (0; +∞);
2) убывает на открытом луче (-∞;
0) и на луче (0; +∞);
3) не ограничена ;
4)унаиб. не существует, унаим. не
существует;
5)непрерывна на луче (-∞; 0) и на
луче (0; +∞) ;
6)Е (y) = (-∞;2) U (2; +∞);
7)выпукла вверх на луче (-∞; 0);
выпукла вниз на луче (0; +∞).
−3
г) у =
x
1)D (y) = (-∞;0) U (0; +∞);
Проверка усвоенного
материала.
2) убывает на открытом луче (-∞;
0) и на луче (0; +∞);
3) не ограничена ;
4)унаиб. не существует, унаим. не
существует;
5)непрерывна на луче (-∞; 0) и на
луче (0; +∞) ;
6)Е (y) = (-∞;0) U (0; +∞);
7)выпукла вверх при х > 0;
выпукла вниз при х < 0.
№10.21.(б,в):
б) у = -3х2 + 6х + 2
унаиб. = 5; унаим. не существует.
в) у = - ‫׀‬х‫׀‬
унаиб. = 0; унаим. не существует.
4.
Ребята, запишите, пожалуйста, домашнее
задание.
Постройте и прочитайте график функции.
№ 10.17.
а) у = 2х + 3
1) D (y) = (-∞; +∞);
2) возрастает;
3)не ограничена;
4) нет наибольшего и наименьшего значений;
5) непрерывна;
6) Е (y) = (-∞; +∞);
7) о выпуклости говорить нет смысла.
б) у = х2
1)D (y) = (-∞; +∞);
2)убывает на луче (-∞; 0], возрастает на луче
[0; +∞);
3)ограничена снизу;
4)унаим. = 0; унаиб. не существует;
Ребята записывают в дневник.
Домашнее задание
записано на доске.
5)непрерывна;
6)Е (у) = [0; +∞);
7)выпукла вниз.
5.
Учитель выясняет, кому не понятно, как
выполнять домашнее задание.
Учитель подводит итог урока и задает классу
вопросы:
- Что закрепляли на уроке?
- Какие затруднения испытывали при
выполнении заданий?
Учитель выставляет оценки за работу на
уроке. Благодарит за урок: «Всем спасибо.
Урок окончен. До свидания!»
Отвечают на вопросы учителя.
Рефлексия.