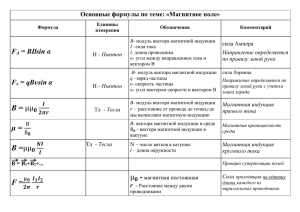
Электромагнитное поле

Элементы теории электромагнитного поля
Электрическое поле – это особый вид материи,посредством которой
осуществляется взаимодействие электрических зарядов.Силовой
характеристикой электрического поля является напряженность Е,
которая численно равна силе, действующей на единичный
положительный заряд, помещенный в данную точку поля:
E=
F
q
(Н Кл –1 = В м –1)
Напряженность – вектор, направленный от (+) к (-). Принцип
суперпозиции позволяет находить напряженность поля,
создаваемого несколькими зарядами, как векторную сумму
напряженностей, создаваемых отдельными зарядами:
n
E=  Ei
i 1
Энергетической характеристикой электрического поля является
потенциал. Потенциал электрического поля в данной точке – это
работа по переносу единичного, положительного, точечного заряда
из точки, потенциал которой принят равным нулю ( обычно этой
точкой является бесконечность), в данную точку поля:
a 
A, а
q
(Дж Кл –1 = В)
Разностью потенциалов (напряжением ) между точками поля
называют работу, производимую силами поля по перемещению
единичного,положительного, точечного заряда из одной точки поля
в другую:
U=    2  1 
2
A
= El dl . Здесь El –проекция вектора
q 1
напряженности поля Е на перемещение dl .Отсюда видно,что
работа по замкнутому пути в электростатическом поле
А =  Fl dl =0, а работа перемещения заряда между двумя точками не
зависит от формы пути. Такое поле называется потенциальным. Т.к.
работа переходит в какой-либо вид энергии, то можно дать
определение потенциала как величины энергии единичного,
положительного заряда, помещеного в данную точку поля:  
Работа dA = F dx, если разделить на q, то
dA Fdx
=
, dφ = E dx
q
q
градиенту потенциала.
E=
W
.
q
d
, т.е. напряженность поля равна
dx
В однородном электрическом поле E=
U
, где d- расстояние между
d
точками с разностью потенциалов U.
В диэлектрике напряженность электрического поля меньше, чем в
вакууме.Относительной диэлектрической проницаемостью среды
ε называется величина, показывающая во сколько раз ослабляется
поле в диэлектрике: ε =
Е0
, где Е0-напряженность поля в вакууме, а
Е
Е-напряженность поля в среде.
Та область пространства, где имеется электрическое поле, содержит
энергию. Объемная плотность энергии электрического поля равна:
we =
We
 E 2
= 0 (Дж м-3), где  0 = 8,85 10-12 ( Ф м-1) – абсолютная
V
2
диэлектрическая проницаемость вакуума, Е- напряженность поля в
среде.
Емкость.
Если на проводник поместить заряд, возникнет поле с потенциалом
φ и отношение
q

зависит лишь от геометрии проводника и
называется емкостью проводника. С 
q  Кл

Фарада  Ф . Другими

B

словами, емкостью проводника называется способность проводника
накапливать заряды. Два проводника, разделенных диэлетриком,
образуют конденсатор, который также характеризуется емкостью.
q
q
 , где Δφ = U – разность потенциалов или напряжение на
 U
 S
коденсаторе. Емкость плоского конденсатора C  0 , где S –
d
С
площадь пластин конденсатора и d – расстояние между пластинами.
Емкость шарового конденсатора С=  0 R, где R-радиус шара.
Если конденсаторы соединяются друг с другом последовательно ,
то q1  q2 , а общее напряжение U  U1  U 2 .
Общая емкость соединения
1
1 1
= +
С С1 С 2
Если конденсаторы соединяются параллельно U1  U 2 , общий заряд
q = q1 +q2. Общая емкость соединения С = С1+ С2.
Энергия электрического поля конденсатора Wконд.= СU
2
.
Если в проводящей среде приложить разность потенциалов
(напряжение), в среде пойдет ток проводимости. Ток проводимости
– это направленное движение электрических зарядов под действием
электрического поля. Численно он равен заряду, проходящему через
поперечное сечение проводника за единицу времени:
dq
U
(Кл с-1=А). Ток проводимости подчиняется закону Ома I= ,
dt
R
U B
l
R – характеристика проводника: R = [  Ом ], R = ρ , l - длина
I A
S
I
проводника, S – площадь его поперечного сечения, ρ- удельное
сопротивление. ρ =
RS
Ом.м зависит от вещества и температуры.
l
При последовательном соединении проводников: I1 = I2
U = U1 +U2, общее R = R1+R2.
При параллельном соединении проводников: I = I1+I2, U1 = U2
Общее
1
1
1


R R1 R2
Плотность тока проводимости j пр =
I
, S – площадь поперечного
S
сечения проводника. j пр = λЕ, Е – напряженность, λ – удельная
электропроводность (уд. Проводимость) проводника.
λ=
1 1
Сименс См 



  Ом.м
м
м 
Магнитное поле – особый вид материи, посредством которой
осуществляется взаимодействие движущихся электрических
зарядов (токов).
1) Действие магнитного поля на рамку с током (замкнутый ток).
Такой ток имеет характеристику «магнитный момент Рm». Он равен
произведению тока в рамке I на ее площадь S. Pm = IS . Магнитный
момент – вектор, направление которого определяется по правилу
винта. Если рамку с током поместить в магнитное поле, то на нее
будет действовать момент пары сил, который поворачивает рамку
так, чтобы вектор Рm совпал с силовой характеристикой магнитного
поля. Силовой характеристикой магнитного поля является вектор
магнитной индукции B 
M max  Н . м

 Тесла  Тл 
2

Pm  А. м

Мmax – максимальный момент сил, действующий на рамку с током,
равный произведению силы на плечо.
2), Действие магнитного поля на прямолинейный токI, длиной l.
Сила ампера.
Сила ампера FA  BI l, отсюда другое определение вектора
магнитной индукции В =
FA  Н

 Тл

Il  Ам

3). Действие магнитного поля на движущийся заряд. Сила Лоренца.
Fл  qVB q – заряд V – скорость заряда, B – вектор магнитной
индукции. Сила Ампера, ток и вектор магнитной индукции, а
следовательно и сила Лоренца, скорость и вектор магнитной
индукции – три взаимноперпендикулярных вектора, поэтому работа
по перемещению в магнитном поле по замкнутому пути не равна
нулю. Такое поле называется вихревым.
В веществе (магнетике) магнитная индукция изменяет свое
значение: В = μ В0, где μ – относительная магнитная
проницаемость,В0 – магнитна индукция поля в вакууме. Величина
Н=
Ам  называется напряженностью магнитного поля. Здесь

В
1
0
μ0 = 4π10-7 (Гн м-1) – абсолютная магнитная проницаемость в
вакууме. Напряженность поля соленоида: Н = I n, где I – ток в
солениде, n – количество витков, отнесенных к единице длины
N
. Объемная плотность энергии магнитного поля в среде:
l
W
 H 2
B2
wm = m  0 
[Дж м-3]
V
2
20 
n=
Явление электромагнитной индукции.
Было доказано Фарадеем , что переменное во времени магнитное
поле порождает электрическое поле , но не стационарное , а
вихревое, т.е. переменное по координате. Работа по перемещению
заряда в таком полепо замкнутому контуру А= LF dx не равна
нулю. Величина такой работы, в расчете на единичный
положительный заряд, называется электродвижущей силой (ЭДС)
Е=
A

q

L
Fdx
  Edx
L
q
Поток магнитной индукции ФВ=  Bn dS , где Вn- нормальная
составляющая вектора В на поверхности S. Для однородного поля
поток магнитной индукции ФВ=B S cos α [Тл м2=Вебер=Вб], где
α- угол между В и нормалью к плоскости S.
Закон электромагнитной индукции Фарадея.
(ЭДС) Е= -
dФВ
dt
При изменении магнитного поля по времени
возникает вихревое электрическое поле , ЭДС которого равна
скорости изменения потока вектора магнитной индукции. Знак
минус выражает правило Ленца , инерционность любой формы
материи: вещества и поля. Частным случаем явления
электромагнитной индукции является явление самоиндукции: если
имеется переменный по времени электрический ток, он создает
вихревое электрическое поле , т.е. ЭДС , которая называется ЭДС
dI
. ЭДС самоиндукции прямо
dt
dI
пропорциональна скорости изменения тока
. L- индуктивность ,
dt
самоиндукции: Е си = -L
характеристика проводника , зависящая от его геометрии и среды :
L=
ВС
Edt
=[
=Ом С]
А
dI
Энергия магнитного поля в индуктивности :
Wm=
LI 2
.
2
Количественной мерой явления порождения вихревого магнитного
поля переменным по времени электрическим полем является ток
dФд
, где ФД – поток
dt
вектора электрической индукции D=ε0 ε Е, ФД =  Dn dS . Плотность
смещения, введенный Д. Максвеллом: Iсм =
тока смещения : јсм =
I см dD
dE

= ε0 ε
.
S
dt
dt
Интегральные основные уравнения Максвелла.
1).
 Edl  
L
dФВ
- это закон электромагнитной индукции, запись
dt
того положения ,что переменное по времени магнитное поле
порождает вихревое электрическое поле. Или : существует вихревое
электрическое поле , источником которого является переменное по
времени магнитное поле.
2).
 Hdl  I полный
L
Iполный = Iпр + Iсм , где Iпр - ток
проводимости – движение зарядов, Iсм – ток смещения – переменное
по времени электрическое поле. Следовательно , источниками
магнитного поля являются движущиеся заряды и переменное по
времени электрическое поле.
3).

S
n
DdS   qi
Поток вектора электрической индукции D через
i 1
замкнутую поверхность S равен алгебраической сумме свободных
электрических зарядов, охватываемых этой поверхностью (теорема
Гаусса- Остроградского). Следовательно, источником
потенциального электрического поля являются свободные заряды.
4). SBdS  0
Поток вектора магнитной индукции сквозь замкнутую
поверхность равен нулю. Следовательно, в природе нет
потенциального магнитного поля , т.к. нет свободных магнитных
зерядов.
Уравнения Максвелла утверждают неразрывную связь
переменных электрических и магнитных полей и возможность их
распространения , т.е. существование электромагнитных волн.