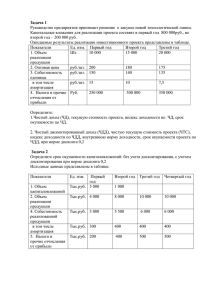
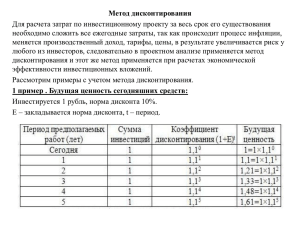
РГЗ "Расчёт эффективности инвестиций"

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Кафедра «Строительство и Архитектура»
Методические указания для выполнения расчетно-графического
задания по дисциплине «Инвестиционный менеджмент» для студентов
специальностей 270103 «Промышленное и гражданское строительство»
270105, «Городское строительство и хозяйство» для очной формы обучения.
Комсомольск – на – Амуре
2013
Расчёт эффективности инвестиций: методические указания для
выполнения расчетно-графического задания по дисциплине
«Инвестиционный менеджмент» / сост. : Е.О. Сысоев, А. Р. Валеев. –
Комсомольск-на-Амуре : ФГОУ ВПО «КнАГТУ», 2013. – 14 с
Данные методические указания включают в себя теоретический
материал и в качестве примера приводятся расчеты эффективности
инвестиций, выполнение которого необходимо для аттестации студентов в
соответствии с рабочей программой курса.
Предназначена для студентов специальностей 270103 «Промышленное
и гражданское строительство» 270105, «Городское строительство и
хозяйство».
Печатается по постановлению редакционно-издательского совета
ФГОУ ВПО «Комсомольского-на-Амуре государственного технического
университета»
Согласовано с отделом менеджмента качества.
Рецензент В.А. Дзюба
1. Введение
Основные показатели экономической эффективности инвестиционных
решений.
К – располагаемые денежные средства.
П – прибыль.
Д – доход, в состав дохода входит прибыль и амортизационные
отчисления.
Ао – амортизационные отчисления, денежные средства выделяемые на
обновление технологического оборудования. Амортизационные отчисления
определяются линейным способом, т.е начисляются равными долями в
течении всего срока эксплуатации оборудования.
i – процентная ставка компенсирует кредиторам те предполагаемые
доходы которые я бы получил реализуя отданные в долг денежные
средства. (в расчёте эффективности инвестиций, принимаем минимальную
процентную ставку сбербанка России 10%)
ДД – дисконтированный доход, доход в котором учтено обесценивание
денежных средств, в связи с получением дохода через t лет.
ДД 
Д
(1  i ) t
ЧДД – чистый дисконтированный доход, который получается
вычитанием из суммы дисконтированных доход в первоначальные
капиталовложения.
ВСД – внутренняя ставка доходности для ряда потоков денежных
средств, представленных их численными значениями, находиться она с
помощью программы Microsoft Excel, вводятся данные в таком порядке как
показано ниже, в скобках расшифровка обозначений, вводить их не надо,
далее выбираем вставить функцию, категория финансовые, в Excel-е она
обозначается как ВСД, в значениях выбираем заполненный нами столбик, и
получаем % ВСД, в данном случае он будет равен 17%
-90 (-К)
32,73(ДД 1год)
29,75(ДД 2год)
27,05(ДД 3год)
24,59(ДД 4год)
22,35 (ДД 5год)
Задача на расчетно-графическое задание: Для оказания услуг жилищнокоммунальным хозяйством приобретено оборудование на сумму x рублей.
Предлагается, что прибыль будет получена в размере y % от вложенного
капитала, при сроке амортизации 5 лет. Определить чистый доход и
внутреннюю норму доходности от реализации проекта.
Номер варианта задания выбирается по последней цифре зачетной
книжке.
Вариант
1
2
3
4
5
6
7
8
9
0
Сумма на
приобретения
оборудование, x
40 000 000 руб.
50 000 000 руб.
60 000 000 руб.
70 000 000 руб.
80 000 000 руб.
40 000 000 руб.
50 000 000 руб.
60 000 000 руб.
70 000 000 руб.
80 000 000 руб.
Предполагаемая
прибыль, y
25%
25%
25%
25%
25%
20%
20%
20%
20%
20%
2. Пример выполнения расчетно-графического задания
Пример задания и решение разными способами: Для оказания услуг
жилищно-коммунальным хозяйством приобретено оборудование на сумму 90
000 000 рублей. Предлагается, что прибыль будет получена в размере 20% от
вложенного капитала, при сроке амортизации 5 лет. Определить чистый
доход и внутреннюю норму доходности от реализации проекта.
2.1 Линейный способ
Вычисления произведём в табличной форме.
Годы
К
Д
Процентная
ставка i
ДД
ЧДД
ВСД
ЧДД при ВСД
0
-90
-
10%
-
-
17%
-
1
36,000
1,10
32,73
-57,27
1,17
30,77
2
36,000
1,21
29,75
-27,52
1,37
26,28
3
36,000
1,33
27,05
-0,47
1,60
22,5
4
36,000
1,46
24,59
24,12
1,87
19,25
5
36,000
1,61
22,35
46,47
2,19
16,416
25,17
-4,199
Сумма ЧДД при
ВСД-К=
Д: 1-год:
2-год:
3-год:
4-год:
5-год:
136,47
Д  П  Ао  К  0,2  К  0,2  90  0,2  90  0,2  36 млн.
Д  П  Ао  К  0,2  К  0,2  90  0,2  90  0,2  36 млн.
Д  П  Ао  К  0,2  К  0,2  90  0,2  90  0,2  36 млн.
Д  П  Ао  К  0,2  К  0,2  90  0,2  90  0,2  36 млн.
Д  П  Ао  К  0,2  К  0,2  90  0,2  90  0,2  36 млн.
i: 1-год: (1  0,1) t  (1  0,1)1  1.1
2-год: (1  0,1) t  (1  0,1) 2  1.21
3-год: (1  0,1) t  (1  0,1) 3  1.33
4-год: (1  0,1) t  (1  0,1) 4  1.46
5-год: (1  0,1) t  (1  0,1) 5  1.61
ДД: 1-год:
Сумма ЧДД при ВСД=
Д
36

 32.73 млн.
t
(1  i )
(1  0.1)1
115,17
Д
(1  i ) t
Д
3-год:
(1  i ) t
Д
4-год:
(1  i ) t
Д
5-год:
(1  i ) t
2-год:
36
(1  0.1) 2
36

(1  0.1) 3
36

(1  0.1) 4
36

(1  0.1) 5

 29.75 млн.
 27.05 млн.
 24.59 млн.
 22.35 млн.
ЧДД: 1-год: ДД  К  32,73  90  57,27 млн.
2-год: ЧДД1  ДД 2  57,27  29,75  27,52 млн.
3-год: ЧДД 2  ДД 3  27,52  27,05  0,47 млн.
4-год: ЧДД 3  ДД 4  0,47  24,59  24,12 млн.
5-год: ЧДД 4  ДД 5  24,12  22,35  46,47 млн.
ВСД:1-год: (1  0,17) t  (1  0,17)1  1.17
2-год: (1  0,17) t  (1  0,17) 2  1.37
3-год: (1  0,17) t  (1  0,17) 3  1,60
4-год: (1  0,17) t  (1  0,17) 4  1,87
5-год: (1  0,17) t  (1  0,17) 5  2.19
ЧДД при ВСД:
Д
36

 30.7 млн.
t
(1  iВСД )
(1  0.17)1
Д
36
2-год:

 26.28 млн.
t
(1  iВСД )
(1  0.17) 2
Д
36
3-год:

 20.8 млн.
t
(1  iВСД )
(1  0.17) 3
Д
36
4-год:

 19.25 млн.
t
(1  iВСД )
(1  0.17) 4
Д
36
5-год:

 16.416 млн.
t
(1  iВСД )
(1  0.17) 5
1-год:
По результатам вычисления строим график.
2.2 Способ остатка
Вычисления произведём в табличной форме.
Годы
Д
К
П + Ао
П
Ао
Процентная
ставка i
ДД
ЧДД
ВСД
ЧДД
при
ВСД
0
90
-
20%
40%
10%
-
-
21%
-
1
54,000
54,000
18
36,000
1,10
49,09
40,91
1,21
44,628
2
32,400
39,600
18
21,600
1,21
32,73
-8,18
1,47
22,04
3
19,440
30,960
18
12,960
1,33
23,26
15,08
1,77
10,983
4
11,664
25,776
18
7,776
1,46
17,61
32,68
2,14
5,45
5
6,998
22,666
18
4,666
1,61
14,07
46,76
2,58
2,7
136,76
Сумма ЧДД при
ВСД=
Сумма ЧДД при ВСД-К=
4,199
Сумма ДД=
П: 1-год: К  0,2  90  0,2  18 млн.
2-год: К  0,2  90  0,2  18 млн.
85,801
3-год: К  0,2  90  0,2  18 млн.
4-год: К  0,2  90  0,2  18 млн.
5-год: К  0,2  90  0,2  18 млн.
Ао: 1-год: К  0,4  90  0,4  36 млн.
2-год: К  0,4  90  0,4  21,6 млн.
3-год: К  0,4  90  0,4  12,96 млн.
4-год: К  0,4  90  0,4  7,776 млн.
5-год: К  0,4  90  0,4  4,666 млн.
К: 1-год: К  Ао1  90  36  54 млн.
2-год: К1  Ао 2  54  21,6  32,4 млн.
3-год: К 2  Ао3  32,4  12,96  19,44 млн.
4-год: К 3  Ао 4  19,44  7,776  11,664 млн.
5-год: К 4  Ао5  11,664  4,666  6,998 млн.
i: 1-год: (1  0,1) t  (1  0,1)1  1.1
2-год: (1  0,1) t  (1  0,1) 2  1.21
3-год: (1  0,1) t  (1  0,1) 3  1.33
4-год: (1  0,1) t  (1  0,1) 4  1.46
5-год: (1  0,1) t  (1  0,1) 5  1.61
ДД: 1-год:
2-год:
3-год:
4-год:
5-год:
П  А0
(1  i ) t
П  А0
(1  i ) t
П  А0
(1  i ) t
П  А0
(1  i ) t
П  А0
(1  i ) t
54
 49,09 млн.
(1  0.1)1
39,6

 32,73 млн.
(1  0.1) 2
30,96

 23,26 млн.
(1  0.1) 3
25,776

 17,61 млн.
(1  0.1) 4
22,666

 14,07 млн.
(1  0.1) 5

ЧДД: 1-год: ДД  К  49,09  90  40,91 млн.
2-год: ЧДД1  ДД 2  40,91  32,73  8,18 млн.
3-год: ЧДД 2  ДД 3  8,18  23,26  15,08 млн.
4-год: ЧДД 3  ДД 4  15,08  17,61  32,68 млн.
5-год: ЧДД 4  ДД 5  32,68  14,07  46,76 млн.
ВСД:1-год: (1  0,21) t  (1  0,21)1  1.21
2-год: (1  0,21) t  (1  0,21) 2  1.47
3-год: (1  0,21) t  (1  0,21) 3  1,77
4-год: (1  0,21) t  (1  0,21) 4  2,14
5-год: (1  0,21) t  (1  0,21) 5  2.58
ЧДД при ВСД:
Д
54

 44,628 млн.
t
(1  iВСД )
(1  0.21)1
Д
32,400
2-год:

 22,04 млн.
t
(1  iВСД )
(1  0.21) 2
Д
19,440
3-год:

 10,983 млн.
t
(1  iВСД )
(1  0.21) 3
Д
11,664
4-год:

 5,45 млн.
t
(1  iВСД )
(1  0.21) 4
Д
6,998
5-год:

 2,7 млн.
t
(1  iВСД )
(1  0.21) 5
1-год:
По результатам вычисления строим график.
2.3. Метод суммы лет
 ЛЕТ  5  4  3  2  1  15лет .
1-год: 5/15=0,33
2-год: 4/15=0,27
3-год: 3/15=0,2
4-год: 2/15=0,13
5-год: 1/15=0,06
Абсолютная сумма амортизации (А):
1-год: 0,33*90=29,7 млн.
2-год: 0,27*90=24,3 млн.
3-год: 0,2*90=18 млн.
4-год: 0,13*90=11,7 млн.
5-год: 0,06*90=5,4 млн.
Вычисления произведём в табличной форме:
Д
Годы
К
П+А
П
А
Процентная
ставка i
ДД
ЧДД
ВСД
ЧДД
при
ВСД
0
-90
-
20%
-
10%
-
-
21%
-
1
-90
47,700
18
29,700
1,10
43,36
46,64
1,21
39,42
2
-90
42,300
18
24,300
1,21
34,96
11,68
1,47
28,78
3
-90
36,000
18
18,000
1,33
27,05
15,37
1,77
20,33
4
-90
29,700
18
11,700
1,46
20,29
35,66
2,14
13,9
5
-90
23,400
18
5,400
1,61
14,53
50,18
2,58
9,06
Сумма ЧДД при ВСДК=
21,41
Сумма ДД=
i: 1-год: (1  0,1) t  (1  0,1)1  1.1
2-год: (1  0,1) t  (1  0,1) 2  1.21
3-год: (1  0,1) t  (1  0,1) 3  1.33
4-год: (1  0,1) t  (1  0,1) 4  1.46
5-год: (1  0,1) t  (1  0,1) 5  1.61
П  А0
47,7

 43,36 млн.
t
(1  i )
(1  0.1)1
П  А0
42,3

 34,96 млн.
2-год:
t
(1  i )
(1  0.1) 2
П  А0
36

 27,05 млн.
3-год:
t
(1  i )
(1  0.1) 3
ДД: 1-год:
140,18
Сумма ЧДД при
ВСД=
111,41
П  А0
29,7

 20,29 млн.
t
(1  i )
(1  0.1) 4
П  А0
23,400

 14,53 млн.
5-год:
t
(1  i )
(1  0.1) 5
4-год:
ЧДД: 1-год: ДД  К  43,36  90  46,64 млн.
2-год: ЧДД1  ДД 2  46,64  34,96  11,68 млн.
3-год: ЧДД 2  ДД 3  11,68  27,05  15,37 млн.
4-год: ЧДД 3  ДД 4  15,37  20,29  35,66 млн.
5-год: ЧДД 4  ДД 5  35,66  14,53  50,18 млн.
ВСД: 1-год: (1  0,21) t  (1  0,21)1  1.21
2-год: (1  0,21) t  (1  0,21) 2  1.47
3-год: (1  0,21) t  (1  0,21) 3  1,77
4-год: (1  0,21) t  (1  0,21) 4  2,14
5-год: (1  0,21) t  (1  0,21) 5  2.58
ЧДД при ВСД:
Д
47,7

 39,42 млн.
t
(1  iВСД )
(1  0.21)1
Д
42,3
2-год:

 28,78 млн.
t
(1  iВСД )
(1  0.21) 2
Д
36
3-год:

 20,33 млн.
t
(1  iВСД )
(1  0.21) 3
Д
29,7
4-год:

 13,9 млн.
t
(1  iВСД )
(1  0.21) 4
Д
23,4
5-год:

 9,06 млн.
t
(1  iВСД )
(1  0.21) 5
1-год:
ИТОГ: (ЧДД при ВСД )  К  111,41  90  21,41 млн.
По результатам вычисления строим график.
3. Список используемой литературы
1. Теплова, Т.В. Инвестиции : учебник / Т.В.Теплова - М. : Юрайт, 2011. - 724
с.
2. Плотников, А.Н. Экономика строительства : учебное пособие / А.Н.
Плотников - М. : Инфра-М, 2012. - 288 с.
3. Экономика: учебник / под ред. В.П. Бардовский, О.В Рудакова, Е.М.
Самородова – М. : Инфра-М, 2011. - 672 с.
4. Управление инвестиционными строительными проектами на основе
Primavera: учебное пособие / под ред. С. В. Бовтеев и др. – СПб.: СПбГАСУ,
2008. - 464 с
СОДЕРЖАНИЕ
1. Введение……………………………………………………………...….3
2. Пример выполнения расчетно-графического задания………………..5
2.1 Линейный способ …................................................................................5
2.2 Способ остатка…………………………………………………………7
2.3 Метод суммы лет………………………………………………….…...9
3. Список используемой литературы…………………………………....13
Дополнительные вопросы на зачет, которые должны быть рассмотрены
по данной дисциплине:
1. Понятие инвестиций, классификация инвестиций.
2. Понятие и этапы инвестиционного процесса.
3. Классификация инвестиций по типу решаемых с их помощью задач.
4. Понятие капитальных вложений, их значение для развития фирмы.
5. Этапы планирования инвестиций.
6. Расчет ставки дисконтирования.
7. Значение показателя рентабельности инвестиций.
8. Амортизионый фонд.
9. Влияние инфляции на оценку инвестиционных проектов.
10. Аренда и лизинг.
11. Классификация инвестиционных рисков.
12. Источники финансирования инвестиций.
13. Виды кредитования инвестиционных проектов.
14. Условия и показатели кредитных соглашений.
15. Факторинг как вид кредитования.
16. Форфейтинг как вид кредитования.
17. Инвестиционные качества облигаций.
18. Определение цены и доходности ценных бумаг.
19. Риски на рынке ценных бумаг.
20. Виды инвестиционных фондов.
21. Венчурные фонды.
22. Инвестиционный проект.
23. Все понятия применяемые в РГЗ.