С 5.
реклама
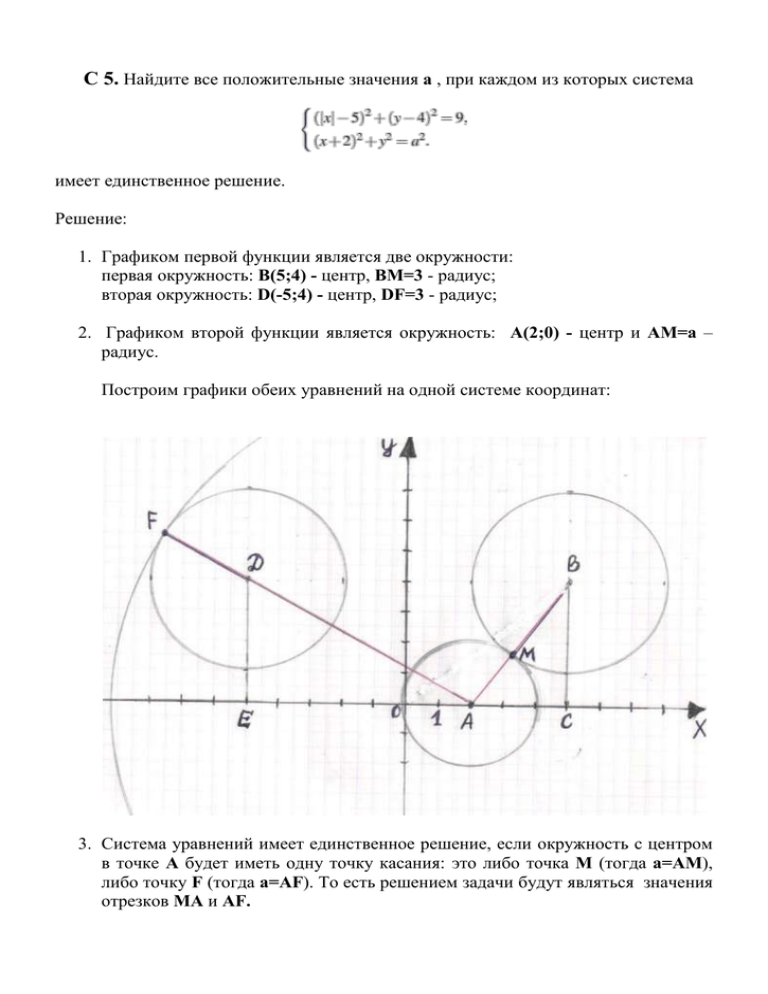
С 5. Найдите все положительные значения a , при каждом из которых система имеет единственное решение. Решение: 1. Графиком первой функции является две окружности: первая окружность: В(5;4) - центр, ВМ=3 - радиус; вторая окружность: D(-5;4) - центр, DF=3 - радиус; 2. Графиком второй функции является окружность: A(2;0) - центр и AМ=а – радиус. Построим графики обеих уравнений на одной системе координат: 3. Система уравнений имеет единственное решение, если окружность с центром в точке А будет иметь одну точку касания: это либо точка М (тогда а=АМ), либо точку F (тогда а=AF). То есть решением задачи будут являться значения отрезков МА и АF. 4. Треугольник АВС прямоугольный, где АВ2 = АС2 + ВС2, откуда АВ2 = 9 + 16, АВ = 5. 5. Найдем значение параметра а: АМ=АВ – ВМ, АМ= 5 – 3 = 2, т.е а=2. 6. Треугольник АDЕ прямоугольный, где АD2=АЕ2 + DЕ2, откуда имеем: АD2=72+42, АD=√65. 7. Найдем значение отрезка АF: АF=АD+DF, т.е а=√65+3 Ответ: а=2, а=3+√65. Для подготовки к ЕГЭ советую решить подобные задачи: Задача 1. Найдите все положительные значения a , при каждом из которых система имеет единственное решение. Задача 2. Найдите все положительные значения a , при каждом из которых система имеет единственное решение.







