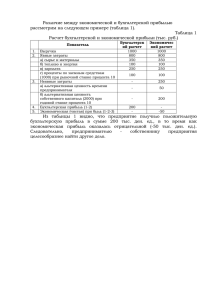
Индивидуальные задания 4

Задачи на применение производной в экономике
1. Объем продукции u, произведенный бригадой рабочих, может быть описан
уравнением u = (-5/6)t3 + (15/2)t2 + 100t + 50 (ед.), [1;8]эt, где t - рабочее время в часах.
Вычислить производительность труда, скорость и темп ее изменения через час после
начала работы и за час до ее окончания.
2. Первоначальный вклад, положенный в банк под 10% годовых, составил 6 млн. руб.
Найти размер вклада через 5 лет при начислении процентов: а) ежегодном; б)
поквартальном; в) непрерывном.
3. Зависимость между издержками производства y и объемом выпускаемой продукции x
выражается функцией y = 50x - 0,05x3 (ден. ед.). Определить средние и предельные
издержки при объеме продукции 10 ед. Ответ: 45 ден. ед.; 35 ден. ед.
4. Объем продукции u (усл. ед.) цеха в течение рабочего дня представляет функцию
u = -t3 - 5t2 + 75t + 425, где t - время (ч.). Найти производительность труда через 2 ч. после
начала работы. Ответ: 43 ед./ч.
5. Зависимость между издержками производства y (ден. ед.) и объемом выпускаемой
продукции x (ед.) выражается функцией y = 10x - 0,04x3. Определить средние и
предельные издержки при объеме продукции, равном 5 ед. Ответ: 9 ден. ед.; 7 ден. ед.
6. Зависимость между себестоимостью единицы продукции y (тыс. руб.) и выпуском
продукции x (млрд. руб.) выражается функцией y = -0,5x + 80. Найти эластичность
себестоимости при выпуске продукции, равном 60 млн. руб.
(Ответ: -0,5)
7. Опытным путем установлены функции спроса q = (p + 8)/(p + 2) и предложения s = p +
0,5 , где q и s - количество товара, соответственно покупаемого и предлагаемого на
продажу в единицу времени, p - цена товара. Найти: а) равновесную цену, т.е. цену, при
которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения
для этой цены; в) изменение дохода при увеличении цены на 5% от равновесной.
(Ответ: a) 2; б) -0,3; 0,8; в) +3,5%.)
8. Функции спроса q и предложения s от цены p выражаются соответственно
уравнениями q = 7 - p и s = p + 1. Найти: а) равновесную цену; б) эластичность спроса и
предложения для этой цены; в) изменение дохода (в процентах) при увеличении цены на
5% от равновесной.
(Ответ: a) 3; б) -0,75; 1; в) +1,25%.)
9. Как связаны предельные и средние полные затраты предприятия, если эластичность
полных затрат равна 1?
(Ответ: y' = ycp (для линейной функции издержек).
10. Цементный завод производит Х т цемента в день. По договору он должен ежедневно
поставлять строительной фирме не менее 20 т цемента. Производственные мощности
завода таковы, что выпуск цемента не может превышать 90 т в день. Определить, при
каком объеме производства удельные затраты будут наибольшими (наименьшими), если
функция затрат имеет вид:
К=-х3+98х2+200х. Удельные затраты составят К/х=-х2+98х+200.
Решение. Наша задача сводится к отысканию наибольшего и наименьшего значения
функции Y= -х2+98х+200.
Таким образом, при выпуске 49 тонн цемента в день удельные издержки максимальны,
это экономически не выгодно, а при выпуске 90 тонн в день минимально, следовательно,
можно посоветовать работать заводу на предельной мощности и находить возможности
усовершенствовать технологию, так как дальше будет действовать закон убывающей
доходности. И без реконструкции нельзя будет увеличить выпуск продукции.
11. Задача о финансовых накоплениях: Предприятие производит Х единиц некоторой
однородной продукции в месяц. Установлено, что зависимость финансовых накоплений
предприятия от объема выпуска выражается формулой f(x)=-0,02x3+600x-1000.
Решение исследуется с помощью производной. Получаем, что при Х=100 функция
достигает максимума.
Вывод: финансовые накопления предприятия растут с увеличением объема производства
до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000
денежных единиц. Дальнейший рост производства приводит к сокращению финансовых
накоплений.
Задачи на применение производной в физике и
технике
1. Колесо вращается так, что угол поворота пропорционален кубу времени. Первые два
оборота сделаны колесом за 2 с. Найдите угловое ускорение через 7 с после начала
вращения. (Угол измеряется в радианах, время – в секундах.)
2. Снаряд массой 4 кг выпущен вертикально вверх из зенитного орудия с начальной
скоростью о = 9,8 м/с. Какова будет кинетическая энергия снаряда через 2 с после начала
движения? На какой высоте кинетическая энергия равна нулю?
3. Величина заряда, протекающего через поперечное сечение проводника, изменяется по
a
закону q = 13,03t +
. Какова будет сила тока в момент времени t = 3 с, если в момент
t 1
времени t = 0 с сила тока равна 12,03А?
t3 t2
4. Материальная точка движется прямолинейно по закону x(t) = - -2t+3 (x изменяется
3 2
в метрах, t – в секундах.) Найдите наименьшее и наибольшее значения x(t) за первые три
секунды движения.