Химия. Практическое занятие по теме: «ЭНЕРГЕТИКА

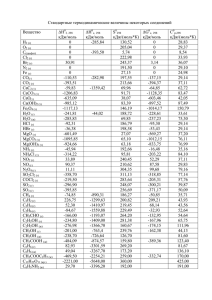
Шкатова Л.А.
Практическое занятие по теме: «ЭНЕРГЕТИКА ХИМИЧЕСКИХ
ПРОЦЕССОВ»
Цель работы: выполнение термодинамических расчётов, связанных с энергетикой
химических реакций.
Сведения из теории
Энергетические эффекты, сопровождающие химические процессы, рассматривает раздел
термодинамики, называемый термохимией. Знание энергетического эффекта реакции даёт
возможность судить о её направлении и пределах самопроизвольного протекания.
В любом процессе соблюдается закон сохранения энергии: теплота q, подведённая к
системе, расходуется на увеличение её внутренней энергии U и на совершение системой работы А
над внешней средой (первый закон термодинамики):
q = U + A
Если химическая реакция протекает в открытом сосуде при постоянной температуре (р, Т –
const) и единственным видом совершаемой работы является работа расширения (A=pV), то
тепловой эффект этой реакции равен изменению энтальпии системы:
qp, T = U + p V, где H = U + pV.
При  Н  0 (когда теплота подводится к системе из окружающей среды) реакцию
называют эндотермической, а при Н  0 (теплота выделяется в окружающую среду) –
экзотермической.
Если в уравнении химической реакции указан её тепловой эффект, уравнение называют
термохимическим. Например:
N2 (г) + 3 Н2 (г) = 2 NH3 (г), Н0298 = – 92,4 кДж
При записи термохимических уравнений реакций указывают: а) агрегатные состояния или
аллотропные модификации веществ; б) условия протекания процессов (Н0298 – стандартный
тепловой эффект реакции при 298 К).
Термохимические расчёты
Закон Гесса. Тепловой эффект реакции зависит от природы и состояния исходных веществ
и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера
промежуточных стадий. Закон Гесса позволяет рассчитать изменение энтальпии химических
реакций. Согласно следствию из закона Гесса, тепловой эффект реакции Н0х.р. равен сумме
теплот образования Н0обр. продуктов реакции за вычетом суммы теплот образования исходных
веществ, с учётом стехиометрических коэффициентов:
Н0х.р. =  Н0обр. (прод.) –  Н0обр. (исх.)
Самопроизвольно процессы протекают в сторону уменьшения Н , то есть при Н  0
(экзотермические).
Самопроизвольно могут протекать также реакции, сопровождающиеся не только
выделением, но и поглощением теплоты. Реакции, идущие при данной температуре с выделением
теплоты, при другой температуре проходят с её поглощением. Здесь проявляется тенденция к
единству и борьбе противоположностей. С одной стороны, система стремится к упорядочению
(агрегации), к уменьшению Н; с другой стороны, система стремится к беспорядку (дезагрегации).
Первая тенденция растёт с понижением, а вторая – с повышением температуры. Тенденцию к
беспорядку характеризует величина, которую называют энтропией.
Энтропия S, так же как внутренняя энергия U, энтальпия Н, объём V и другие величины,
является свойством вещества, пропорциональным его количеству. S, U, H, V обладают свойствами
аддитивности, то есть при соприкосновении системы суммируются.
Энтропия отражает движение частиц вещества и является мерой
неупорядоченности системы. Она возрастает с увеличением движения частиц: при нагревании,
испарении, плавлении, расширении газа, при ослаблении или разрыве связи между атомами и т.п.
процессами. Процессы, связанные с упорядочением системы: конденсация, кристаллизация,
сжатие, упрочнение связи, полимеризация и т.п. – ведут к уменьшению энтропии. Энтропия
является функцией состояния, то есть её изменение (S) зависит только от начального (S1) и
конечного (S2) состояний, но не зависит от пути процесса:
Sх.р. =  S0 (прод.) –  S0 (исх.)
Иначе говоря, S = S2 – S1.
Так как энтропия возрастает с ростом температуры, то можно считать, что мера беспорядка
 T S. Энтропия выражается в Дж / моль К. Таким образом, движущая сила процесса
складывается из двух сил: стремления к упорядочению (Н) и стремления к беспорядку (TS). При
постоянных давлении и температуре общую движущую силу процесса G можно найти из
соотношения:
G = (Н2 – Н1) – (TS2 – TS1) = H – TS.
Величина G называется изобарно-изотермическим потенциалом или энергией Гиббса.
Итак, мерой химического сродства является убыль энергии Гиббса (G), которая зависит от
природы вещества, его количества и от температуры. Энергия Гиббса является функцией
состояния, поэтому
Gх.р. =  Gобр.(прод.) –  Gобр. (исх.).
Самопроизвольно протекающие процессы идут в сторону уменьшения потенциала, и, в
частности, в сторону уменьшения G. Если G  0, процесс принципиально осуществим,
если G  0 – процесс самопроизвольно проходить не может. Чем меньше G, тем сильнее
стремление к протеканию данного процесса и тем дальше он от состояния равновесия, при
котором G=0 и Н=ТS.
Из соотношения G = H – TS видно, что самопроизвольно могут протекать и процессы,
для которых Н  0 (то есть эндотермические). Это возможно, когда S 0, но TSН, и тогда
G  0. С другой стороны, экзотермические реакции (когда Н  0) самопроизвольно не
протекают, если при S  0 окажется, что G  0.
Примеры решения задач
Пример 1. Вычислите Н0, S0, G0 химической реакции:
Fe2O3 (К) + 3 C(К) = 2 Fe(К) + 3 СО(Г). Возможна ли эта реакция при 500 и 1000 К?
Решение.
Из табличных данных находим:
Soобр,
Н0обр,
Gообр,
Дж/моль К
кДж/моль
кДж/моль
Fe2O3 (K)
–822,1
89,96
–740,3
C (K)
0
5,69
0
Fe (K)
0
27,2
0
CO (Г)
–110,52
197,91
–137,27
Отсюда:
2
Но х. р. =  Но(прод.) –  Но(исх.) = 2 Но(Fe) + +3 Hо(СО) – (Но(Fe2O3) + 3 Но(С)) =
2х0 + 3х(–110,52) – (–822,1 + 3х0) = 490,54 кДж.
Sох. р. = 2 So(Fe) + 3 Sо(СО) – (So(Fe2O3) + 3So(С)) = = 2х27,2 + 3х197,91 – (89,96 + 3х5,69) =
541,1 Дж / К.
Goх. р. = 2 Go(Fe) + 3 Go(СО) – (Go(Fe2O3) + +3Gо(С)) = 2х0 + 3х(– 137,27) – (740,3 +
3х0) = 328,49 кДж.
Энергия Гиббса при соответствующих температурах находим из уравнения G = H– –
TS.
 G5оо = 490,54 – 500х541,1х10–3 =219,99 кДж.
 G1ооо = 490,54 – 1000х541,1х10–3 = – 50,56 кДж.
Пример 2. Прямая или обратная реакция будет протекать при стандартных условиях в
системе: СН4 (Г) + +СО2(Г)  2 СО(Г) + 2 Н2 (Г).
Решение.
Вывод о самопроизвольном протекании процесса можно сделать, рассчитав Gох. р.
 Gох. р. = 2Gо(СО) + 2 Gо(Н2) – (Gо(СН4) + +Gо(СО2)) = 2х(–137,27) + 2х0 – (–50,79 + (–
394,38)) = =170,63 кДж.
Так как  Gох. р.  0, значит самопроизвольное протекание процесса в прямом направлении
при стандартных условиях невозможно. Так как  Gо298 прямой реакции равна –Gо298 обратной
реакции, то  Gох. р. (обратной) = =–170,63 кДж и такая реакция возможна в стандартных условиях.
Пример 3. Определить тепловой эффект реакции CO2(Г) + MgO (к) = MgCO3 (к).
Решение.
По табличным данным находим:
CO2
–393,5
Нообр.
MgO
–601,8
MgCO3
–1096,21
кДж/моль
Отсюда Нох. р. =Но(MgCO3)–(Нo(MgO)+Но(СО2))= = – 100, 91 кДж. Так как Нох. р.  0,
процесс экзотермический.
Пример 4. Найти тепловой эффект превращения 1 моля водяного пара в жидкую воду, если
образование водяного пара и воды протекает по следующим уравнениям:
Н2 (г) + ½ О2 (г) = Н2О (г) + 241,88 кДж.
Н2 (г) + ½ О2 (г) = Н2О (ж) + 285,91 кДж.
Решение.
Для решения задачи нужно найти Н перехода Н2О(г)Н2О(ж).
Нообр. (Н2О(г)) = – 241,88 кДж/моль.
Нообр. (Н2О(ж)) = – 285,91 кДж/моль.
Н(фаз. перехода) =  Нообр. (Н2О(ж)) – Нообр.(Н2О(г)) = – 285,91 – (– 241,88) = – 44,03
кДж/моль.
При переходе 1 моля водяного пара в жидкость выделяется 44,03 кДж теплоты.
Пример 5. При сгорании 112 л метана выделяется 4012,55 кДж теплоты. Вычислить
о
Н (СН4), зная ,что при реакции выделяются газообразные продукты.
Решение.
Горение метана протекает согласно уравнению
СН4 (Г) + 2 О2 (Г) = СО2 (Г) + 2 Н2О (Г)
= Н (СО2) + 2Н (Н2О) – (Но(СН4) + 2Но(О2)). Отсюда Но(СН4) = Но(СО2) +
2Но(Н2О) – Нох.р. , так как Но (О2) = 0. Так как по уравнению реакции сгорает 1 моль метана, то
Нох.р. = (–4012,55х22,4) / 112 = –802,51 кДж.
о
Тогда Н (СН4) = –393,51 + 2х(–241,83) – (–802,51) = –74,67 кДж/моль.
Нох.р.
о
о
3
Контрольные вопросы и задания
1. Можно ли предсказать влияние температуры на направление химической реакции, если
известна её энтальпия? Ответ подтвердите на примере какой-либо реакции.
2. Возможно ли самопроизвольное окисление азота по уравнению: ½ N2 + O2 = NO2 при
стандартных состояниях веществ при 298 К и других температурах? Ответ подтвердите расчетом.
3. При нейтрализации 0,5 моль КОН соляной кислотой выделилось 27,95 кДж теплоты.
Рассчитайте, сколько молей воды образовалось при этом, и теплоту реакции нейтрализации.
Запишите термохимическое уравнение реакции. /Ответ: –55,9 кДж/.
4. Теплота нейтрализации сильной кислоты сильным основанием при стандартных
условиях равна – 55,9 кДж/моль воды. Вычислите, сколько теплоты выделится при смешении 100
мл 0,5 М раствора соляной кислоты со 100 мл 0,5 М раствора гидроксида натрия. /Ответ: 2,80
кДж/
5. Напишите термохимическое уравнение реакции взаимодействия газообразных аммиака и
хлороводорода. Сколько теплоты выделится в ходе этой реакции, если было израсходовано 100 л
аммиака? /Ответ: 790 кДж/
6. Для реакции димеризации оксида азота (IV) 2NO2=N2O4 Н0298 = – 1387,3 Дж, S0298 = –
42,19 Дж / моль К. При каких температурах димеризация наиболее вероятна?
7. При сгорании 1 л водорода выделяется 12,76 кДж. Рассчитайте энтальпию образования
воды. В каком агрегатном состоянии будет находиться вода в результате этого процесса? /Ответ:
– 285,6 кДж / моль/
8. Определите возможность протекания процесса NH3(г)+ HCl (г) = NH4Cl (к) , исходя из
энтальпийного и энтропийного факторов.
Литература
1. Коровин Н.В. Общая химия. М.: Высшая школа, 2000.
2. Коровин Н.В., Мингулина Э.И., Рыжова Н.Г. Лабораторные работы по химии. М.:
Высшая школа, 1998.
3. Химия. Методические указания, решение типовых задач и контрольные задания для
студентов инженерно-технических специальностей. Ч. 1. М.: 1992.
ПРИЛОЖЕНИЯ
СТАНДАРТНЫЕ ТЕПЛОТЫ
(ЭНТАЛЬПИИ) ОБРАЗОВАНИЯ Н0298
НЕКОТОРЫХ ВЕЩЕСТВ
Вещество
Состояние
С2Н2
CS2
NO
C6H6
C2H4
Н0298
4
Г
Г
Г
Г
Г
кДж/моль
+226,75
+115,28
+90,37
+82,33
+52,28
H2S
BaO
NH3
CH4
C2H6
HCl
TiO2
CO
CH3OH
C2H5OH
H2O
H2O
NH4Cl
BaCO3
CO2
Fe2O3
Ca(OH)2
Al2O3
MgO
Г
Ж
Г
Г
Г
Г
Ж
Г
Г
Г
Г
Ж
К
К
Г
К
К
К
К
-20,15
-558,1
-46,19
-74,85
-84,67
-92,31
-943,9
-110,52
-201,17
-235,31
-241,83
-285,84
-315,39
-1219,0
-393,51
-822,10
-986,50
-1669,80
-601,80
Fe2O3
NH4Cl
CH3OH
H2
Fe3O4
CH4
HCl
C2H5OH
H2O
N2
BaO
CaCO3
NH3
CO
C2H2
O2
H2S
NO
CO2
C2H4
Cl2
NO2
PCl3
PCl5
MgO
C2H6
CaO
СТАНДАРТНЫЕ АБСОЛЮТНЫЕ
ЭНТРОПИИ S0298 НЕКОТОРЫХ ВЕЩЕСТВ
Вещество
C
C
BaCO3
Ca(OH)2
Fe
Ti
S
TiO2
FeO
H2O
Состояние
Алмаз
Графит
К
К
К
К
Ромбич.
К
К
Ж
S0298Дж/моль К
2,44
5,69
112
76,1
27,2
30,7
31,9
50,3
54,0
69,94
5
К
К
Ж
Г
К
Г
Г
Ж
Г
Г
К
К
Г
Г
Г
Г
Г
Г
Г
Г
Г
Г
Г
Г
К
Г
К
89,96
94,5
126,8
130,59
146,4
186,19
186,68
160,7
188,72
191,49
70,3
88,7
192,50
197,91
200,82
205,03
205,64
210,20
213,65
219,45
222,95
240,46
311,66
352,71
26,24
229,5
39,7
СТАНДАРТНАЯ ЭНЕРГИЯ ГИББСА ОБРАЗОВАНИЯ G0298 НЕКОТОРЫХ ВЕЩЕСТВ
Вещество
BaCO3
CaCO3
Fe3O4
BeCO3
CaO
BeO
BaO
CO2
NaCl
ZnO
MgO
FeO
H2 O
H2 O
PbO2
CO
CH4
NO2
NO
C2H2
TiO2
G0298 кДж/моль
-1138,8
-1128,75
-1014,22
-944,75
-604,2
-581,61
-528,4
-394,38
-384,03
-318,20
-569,60
-244,3
-237,19
-228,59
-219,0
-137,27
-50,79
+51,84
+86,69
+209,20
-883,3
Состоя-ние
К
К
К
К
К
К
К
Г
К
К
К
К
Ж
Г
К
Г
Г
Г
Г
Г
К
6