Квантование сопротивления

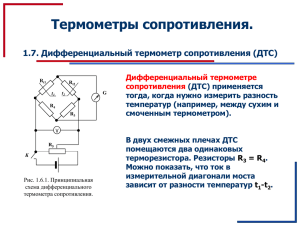
УДК 538.945(06)+539.2(06) Сверхпроводимость и физика наноструктур
А.И. ГОЛОВАШКИН, Л.Н. ЖЕРИХИНА1,
Г.В. КУЛЕШОВА, А.М. ЦХОВРЕБОВ1
Московский инженерно-физический институт (государственный университет)
1Физический институт им. П.Н. Лебедева РАН, Москва, Россия
КВАНТОВАНИЕ СОПРОТИВЛЕНИЯ: СЛЕДЫ ЭФФЕКТА
НА ВАХ ВАКУУМНОГО СВЧ ТРИОДА И ВЫБОР
АДЕКВАТНО ОБЪЯСНЯЮЩЕЙ МОДЕЛИ
В нашем докладе [1] на прошлой сессии МИФИ-2007 сообщалось об обнаружении следов квантования
сопротивления электронного потока в вакуумном СВЧ триоде ГС-13 (рис. 1). В заключение того доклада
было указано на возможность выбора одной из двух альтернативных теоретических моделей квантования
сопротивления посредством проведения измерений интенсивности дробового шума в точке ВАХ, лежащей
на «квантовой полочке» [1]. Однако в ходе подготовки этого весьма непростого эксперимента (регистрация
флуктуаций тока на уровне 50фА/Гц-0,5…) был предложен более легкий способ выбора адекватной модели.
Рассмотрим возможные альтернативы. Первая модель, предложенная Ландауэром [2] объясняет эффект
квантования сопротивления, основы-ваясь на простейших положениях квантово-статистической физики
одно-мерных Ферми систем. Так, электронная плотность состояний в одно-мерном случае есть n F I   1 ,
E
2VF
где VF – фермиевская скорость. Из-за различия электронной плотности, возникающего вследствие разности
химпотенциалов на концах одномерной (т.е. квантоворазмерной в поперечных направлениях) нити
nF I 
I 
eU , разность прямого и обратного электронного потока оказывается ненулевой, в резульnF 
E
eU 
2VF
тате чего возникает макроскопический электрический ток I  eV n  I   e 2U . В итоге отношение разности
F
F
2
потенциалов на концах нити к силе тока можно выразить только через мировые константы, которые определяют квантовый эталон сопротивления R(I)=U/I=2πħ/e2= RQ =25813Ом.
Вторая модель [3,4] основывается на аналогии с нестационарным эффектом Джозефсона. Здесь разность
потенциалов, приложенная к мезоскопическому объекту, вызывает осцилляции тока с «одноэлектонной»
джозефсоновской частотой ωJ=eU/ħ. Когда ωJ совпадает с частотой 1,2,3…n-электронного прохождения через такой объект, происходит резонанс ωJ=ωne→eU/ħ=2πI/ne→R=U/I=2πħ/ne2=RQ/n. Как видно при этом сопротивление объекта R квантуется.
Обсуждая применимость первой модели, мы обратили внимание на то, что при плотностях заряда соответствующих электронному потоку в вакуумном триоде (ne-=106÷107см3) температура вырождения TF составляет примерно 1мкК. Таким образом, электронный газ в потоке является заведомо невырожденным, и в
этом смысле к нему неприменима Ферми статистика, а, следовательно, все выводы, основанные на формулах типа n F I 
1 , в данном случае оказываются абсолютно не оправданными. В итоге, «по методу исE

2VF
ключения» остается вторая модель, согласно которой механизм квантования сопротивления здесь аналогичен нестационарному эффекту Джозефсона.
Рис. 1. Квантование
зависимость проводимоσАС=σАС(UG), а на самом
ной и усредненной зави-
проводимости: на вкладке приведена исходная
сти анод/катод от сеточного напряжения
рисунке представлен график разности исходсимости ΔσАС=σАС-<σAC>
Работа выполнеРАН «Сильно корводниках, металлах,
териалах», а также
научных школ»
на при поддержке программы ОФН
релированные электроны в полупросверхпроводниках и магнитных мапрограммы
«Развитие
ведущих
Список литературы
1. А.И. Головашкин, Л.Н. Жерихина, Г.В. Кулешова,
А.М. Цховребов //
МИФИ-2007, Сборние трудов. Т.4,
C.138.
2. R.Landauer // IBM J. Res. Dev. V.1, P. 223 (1957)
3. А.И. Головашкин, А.Н. Жерихин, Л.Н. Жерихина, Г.В. Кулешова, А.М.Цховребов // Поверхность. Рентг., синхр.
и нейтр. иссл-я. 2005. №10, С.3-15.
4. А.И. Головашкин, А.Н. Жерихин, Л.Н. Жерихина, Г.В. Кулешова, А.М.Цховребов // Краткие сообщения по физике2006. №1. С.23.