1. Исходные данные

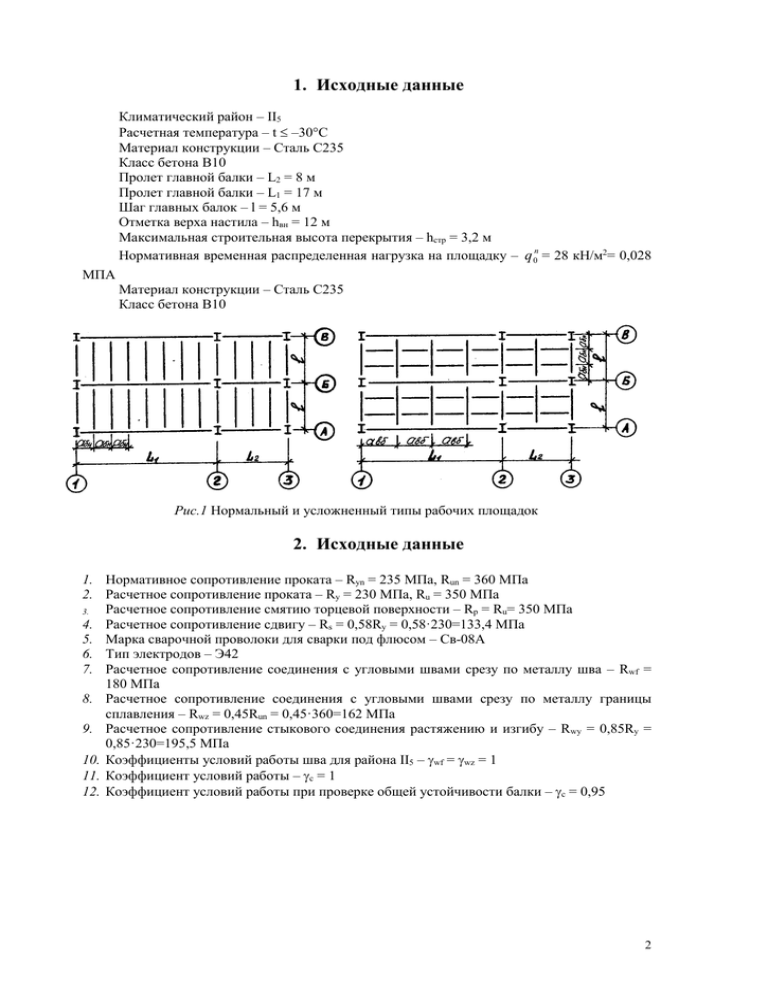
1. Исходные данные
Климатический район – II5
Расчетная температура – t  –30C
Материал конструкции – Сталь С235
Класс бетона В10
Пролет главной балки – L2 = 8 м
Пролет главной балки – L1 = 17 м
Шаг главных балок – l = 5,6 м
Отметка верха настила – hвн = 12 м
Максимальная строительная высота перекрытия – hстр = 3,2 м
Нормативная временная распределенная нагрузка на площадку – q 0n = 28 кН/м2= 0,028
МПА
Материал конструкции – Сталь С235
Класс бетона В10
Рис.1 Нормальный и усложненный типы рабочих площадок
2. Исходные данные
1. Нормативное сопротивление проката – Ryn = 235 МПа, Run = 360 МПа
2. Расчетное сопротивление проката – Ry = 230 МПа, Ru = 350 МПа
Расчетное сопротивление смятию торцевой поверхности – Rp = Ru= 350 МПа
3.
4. Расчетное сопротивление сдвигу – Rs = 0,58Ry = 0,58·230=133,4 МПа
5. Марка сварочной проволоки для сварки под флюсом – Св-08А
6. Тип электродов – Э42
7. Расчетное сопротивление соединения с угловыми швами срезу по металлу шва – Rwf =
180 МПа
8. Расчетное сопротивление соединения с угловыми швами срезу по металлу границы
сплавления – Rwz = 0,45Run = 0,45·360=162 МПа
9. Расчетное сопротивление стыкового соединения растяжению и изгибу – Rwy = 0,85Ry =
0,85·230=195,5 МПа
10. Коэффициенты условий работы шва для района II5 – wf = wz = 1
11. Коэффициент условий работы – с = 1
12. Коэффициент условий работы при проверке общей устойчивости балки – с = 0,95
2
3. Расчет стального настила
В качестве настила балочной площадки используются стальные листы толщиной t = 12
мм при распределительной нагрузки qn0 > 20 кН/м2
Цилиндрическая жесткость настила
E1 
E
= 2,26105 МПа
1  2


где E = 2,0610 МПа – модуль упругости стали
 = 0,3 – коэффициент Пуассона стали
Отношение пролета настила к его толщине при работе настила на изгиб с распором
5
l 4n0  72 E1  4  120  72  2,26  108 
1 

1 
 = 89,68

t 15  n04 q0n 
15 
120 4  28 
где n0 = 120 – отношение пролета настила к его предельному прогибу
qn0 = 28 кН/м2 – заданная нормативная нагрузка на настил
Пролет настила
l 
l     t  89,68  0,012 = 1,08 м
t 
По табл.20 методом интерполяции находим значение n0 , n0 = 121,5
Отношение пролета настила к его толщине при работе настила на изгиб с распором
l 4n0  72 E1  4  121,5  72  2,26  108 
1 

1 
 = 90,8

t 15  n04 q0n 
15 
121,5 4  28 
Пролет настила
l 
l     t  90,8  0,012 = 1,09 м
t 
Шаг балок настила, назначаемый с учетом размеров их поясов (кратен 100 мм)
aбн  l  (80..100)  1100 мм
Усилие на единицу длины сварного шва, прикрепляющего лист к балке настила
 
H   f 1 Et 
 2n0
2

 3,14 
  1,2  2,06  10 8 êÍ  0,012 ì  
 = 507,77 кН/м
 2  121,5 

2
где f1 = 1,2 – коэффициент надежности по временной распределенной нагрузке на площадку
Расчетный катет углового шва, прикрепляющего настил к балкам, определяется по
наибольшему значению
 при расчете по металлу шва
kf 
H
507,77êÍ / ì

 f l w Rwf  wf  c 0,7  1ì  180  10 3 êÍ / ì
2
11
= 0,004м=4 мм
 при расчете по металлу границы сплавления
kf 
H
507,77êÍ / ì

 z l w Rwz  wz  c 1  1  162  10 3 êÍ / ì
2
1 1
= 0,003м=3 мм
где lw = 1 – расчетная длина шва
f = 0,7 и z = 1 – коэффициенты, принимаемые для полуавтоматической сварки в
нижнем положении
Окончательно катет шва кратен 1 мм и принимается kf = 6 мм
3
4. Расчет вспомогательных балок и балок настила
4.1. Нормальный вариант балочной площадки
Нормативная нагрузка на 1 погонный метр балки настила



qáín  1,02aáí q0n  q ín  1,02  1,1ì  28êÍ / ì
2
 78,5êÍ / ì
3

 0,012 ì  32,47 кН/м
где 1,02 – коэффициент, учитывающий собственный вес балки настила
q нn = 78,5t кН/м2 – нормативная распределенная нагрузка от стального настила
Расчетная нагрузка на 1 погонный метр балки настила
qбн  1,02aбн  f 1q0n   f 2 qнn  1,02 1,1м  (1,2  28  1,05  78,5кН / м3  0,012 м)  38,8 кН/м


где f2 = 1,05 – коэффициент надежности по постоянной нагрузке от стального настила
Расчетный изгибающий момент
q áí l 2 38,8êí / ì  5,6 ì
M 

8
8
2
= 152,1 кНм
где l = 5 м – заданный шаг главных балок
Требуемый момент сопротивления
Wn,min 
M
152,1
= 601,1 см3

c1 R y  c 1,1  230  1
где c1 = 1,1 – коэффициент, учитывающий развитие пластических деформаций по сечению
Требуемый момент инерции
I min 
5 qáín l 3 n0
5 32,47  5,6 3  193,3
= 6967 см4


8
384 E
384
2,06  10
где n0 = 193,3 – отношение пролета балки настила к его предельному прогибу
№36 Wx = 743 см3, Ix = 13380 см4, Gбн = 48,6 кг/м,
Расход металла на 1 м2 площади
g  t 
Gáí
48,6
= 138 кг/м2
 7850  0,012 
aáí
1,1
где  = 7850 кг/м3 – плотность стали
Расход металла на площадку
G  2l L1  L2 g = 2·5,6(17+8)·138=38640 кг
Количество отправных элементов (балок настила) – х шт
4.2. Усложненный вариант балочной площадки
Расчет балок настила
Расчетный изгибающий момент
M 
qáí l 2 38,8  3,42

 56,1 кНм
8
8
где l = aвб = 3,4 м – шаг вспомогательных балок настила
Требуемый момент сопротивления
Wn, min 
M
56,1

 221 см3
c1Ry c 1,1  230  1
Требуемый момент инерции
I min 
5 qáín l 3n0 5  32,47  3,43157

 1266 см4
8
384 E
384  2,06  10
№22 Wx = 232 см3, Ix = 2550 см4, Gбн = 24 кг/м, h = 220 мм
Масса балки настила на 1 м2 площади
4
máí 
Gáí 24

= 22 кг/м2
aáí 1,1
Расчет вспомогательных балок настила
Нормативная нагрузка на вспомогательную балку


n
qâá
 1,02aâá q0n  qín  máí  1,02  3,428  78,5  0,012  0,22 = 101,13 кН/м
где 1,02 – коэффициент, учитывающий собственный вес вспомогательной балки
aвб = 3,4 м – шаг вспомогательных балок настила
Расчетная нагрузка на вспомогательную балку


qâá  1,02aâá  f 1q0n   f 2qín   f 2máí  1,02  3,4(1,2  28  1,05  78,5  0,012  0,22 1,05)  120,8êÍ / ì
Расчетный изгибающий момент
qâál 2 120,8  5,62
M 

 = 473,5 кНм
8
8
где l = 5,6 м – заданный шаг главных балок
Требуемый момент сопротивления
Wn,min 
M
473,5
= 1871 см3

c1Ry c 1,1 230 1
Требуемый момент инерции
I min 
n 3
5 qâá
l n0 5 101,13  5,63 193,3
= 21700 см4

384 E
384  2,06 108
№55 Wx = 2035 см3, Ix = 55962 см4, Gбн = 92,6 кг/м, t = 16,5 мм, h = 550 мм
Масса вспомогательной балки на 1 м2 площади
mâá 
Gâá 92,6

= 27,2 кг/м2
aâá
3,4
Расход металла на 1 м2 площади
g  t  máí  mâá  7850  0,012  22  27,2 = 143,4 кг/м2
Расход металла на площадку
G  2l L1  L2 g  2  5,6(17  8) 143,4 = 40152 кг
Количество отправных элементов (балок настила и вспомогательных балок) – 84 шт
2.3. Сравнение вариантов балочной площадки
Вариант
Нормальный
Усложненный
Расход металла, кг
на 1 м2 площадки
на площадку
138
38640
143,4
40152
Количество
элементов, шт
54
84
5
5. Расчет и конструирование главной балки
a.
Расчетная схема. Расчетные нагрузки и усилия
Нормативная погонная нагрузка на
главную балку
q n  1,03l (q0n  g )  1,03  5,6(28  1,38) =
169,4 кН/м
где 1,03 – коэффициент, учитывающий
собственный вес балки
g = 1,38 кН/м2 – расход металла на 1
м2 площадки
Расчетная погонная нагрузка на
главную балку
q  1,03l ( f 1q0n   f 2 g )  1,03  5,6(1,2  28  1,05 1,38)
= 202,16 кН/м
Расчетные усилия
qL12 202,16 17 2

= 7303,03 кНм
8
8
 0,5qL1  0,5  202,16 17 = 718,38кН
M 1 max 
Q1 max
Рис.2 Расчетная схема балок
qL22 202,16  82

= 1620,8 кНм
8
8
 0,5qL2  0,5  202,16  8 = 808,64 кН
M 2 max 
Q2 max
b.
Определение высоты балки
Максимальная высота балки при этажном сопряжении
L1
17
 3,2  0,012  0,36 
= 2,75 м
n0
230,6
L
8
 hстр  t  hбн  2  3,2  0,012  0,36 
= 2,79 м
n0
205,5
h1 max  hстр  t  hбн 
h2 max
где t = 12 мм – толщина настила
hбн = 270 мм – высота балки настила
hстр = 3,2 м – высота вспомогательной балки
n0 – отношение пролета главной балки к ее предельному прогибу
Минимальная высота балки при полном использовании расчетного сопротивления
стали
5 L1Rу n0 q n 5 17  230 103  230,6 169,4

 0,76 м
24 E q
24  2,06 108  202,16
5 L2 Rу n0 q n 5  8  230 103  205,5 169,4
= 0,32 м


24 E
q
24  2,06 108  202,16
h1min 
h2 min
При расчете с учетом пластических деформаций hmin увеличивается на коэффициент c1
= 1,1
Требуемый момент сопротивления сечения балки
M 1 max 7303,03

= 31752 см3
Rу с
230  1
M
1620,8
= 7047 см3
 2 max 
Rу с
230 1
W1 min 
W2 min
6
Оптимальная высота сварной балки переменного сечения в пределах упругих
деформаций
h1  5,53 W1 min  5,63 31752 = 1,74 м
h2  5,53 W2 min  5,53 7047 = 1,05 м
Уточненная оптимальная высота балки
W1 min
31752
= 1,95 м
 1,2
t1w
1,2
h1opt  k
h2opt  k
W2 min
7047
= 1,07м
 1,2
t2 w
1,0
м
где t1w = 12 мм, t2w = 10 мм – толщины стенок
k = 1,2 – коэффициент, зависящий от конструктивного оформления балки
Окончательно высота балки назначается близкой к оптимальной, кратной 100 мм при
соблюдении условия hmin  h  hmax и принимается h1 = 2000 мм, h2 = 1100 мм
c.
Подбор сечения балки
Определение толщины стенки
Минимальная толщина стенки
t w,min  k
Q1max
718,38
= 4,0 мм
 1,5
hRs  c
2 133,4 1
где k = 1,5 – при работе на срез только стенки (без учета поясов)
h = 2м – высота главной балки
Толщина стенки, назначенная в п.3.2., удовлетворяет условиям ее работы на
касательные напряжения на опоре
При высоте балки до 2 м экономически целесообразно назначать толщину стенки с
учетом того, что местная устойчивость стенки без дополнительного укрепления ее
продольным ребром обеспечивается, если соблюдается условие
tw 
hw R y 1,95
230
= 12 мм

5,5 E
5,5 2,06 10 5
где hw = h-50 = 1950 мм – высота стенки балки
Рациональное значение толщины стенки для балок высотой 1..2 м
t w  7  0,003h  7  0,003  2 = 13 мм
где h = 2000 мм – высота главной балки
Если назначенная в п. 6.2 толщина стенки отличается от полученных по формулам
(6.8) и (6.10) более чем на 2 мм, необходимо принять новое её значение (tw  tw,min), затем
вновь вычислить оптимальную высоту балки hopt и скорректировать её высоту h.
7
Определение размеров горизонтальных поясных листов
Требуемый момент инерции сечения балки
I min  0,5Wmin h  0,5  31752  200 = 3175200 см4
Момент инерции стенки балки
t w hw3 1,2  1953
= 741487,5 см4
Iw 

12
12
где hw = 1950 мм – высота стенки балки
Момент инерции, приходящийся на поясные листы
I f ,min  I min  I w = 2433712,5 см4
Требуемая площадь сечения одного поясного листа
A f ,min 
2 I f ,min
h
2
f

2  2433712,5
= 124,2 см2
2
198
где hf = h-20 = 1980 мм – расстояние между центрами тяжести поясов
Требуемая ширина пояса
b f ,min 
A f ,min
tf

12420
= 414мм
30
где tf = 30 мм  3tw = 36 мм – толщина пояса по сортаменту
Для назначения ширины пояса bf проверим выполнение следующих условий

обеспечение общей устойчивости балки
b f  (1 / 3....1 / 5)h 




h 2000

= 500 мм
4
4
конструктивные решения bf  180 мм
расчет bf  bf,min
равномерное распределение напряжений по ширине пояса bf  30tf = 900 мм
обеспечение местной устойчивости пояса
bf  t f
E
2,06  10 5
 t w  30
 12 = 910 мм
Ry
230
Ширина пояса, с учетом стандартной ширины листов универсальной стали,
принимается bf = 450 мм
Определение геометрических характеристик сечения
Площадь пояса
A f  b f t f = 135 см2
где tf = 30 мм
Площадь стенки
Aw  hw t w = 232,8 см2
где hw = h-2tf = 1940 мм
Момент инерции стенки
t w hw3
Iw 
= 730138,4 см4
12
Момент инерции балки
I x  I w  0,5 A f h 2f = 3349745,9 см4
где hf = h-tf = 1970 мм
Момент сопротивления
Wx 
Рис. 3 Сечение балки
2I x
= 33498см3
h
8
Проверка прочности принятого сечения

M 1 max 730303

 R y  c => 21,9  23 кН/см2
Wx
33498
Недонапряжение
 
Ry  
Ry
100% = 4,8% < 5%
Данная балка удовлетворяет проверке на прочность
Проверка прогиба балки
5 q n L14
f  1,2
  f  => 0,0002  0,073
384 EI x
где  f  
L1
= 0,073 – предельный прогиб балки
n0
d. Расчет изменения сечения балки по длине
Сечение балки, подобранное по максимальному моменту, изменяется за счёт
уменьшения ширины поясов на расстоянии примерно 1/6 пролёта балки от опоры, т.е. x 
1
L1
6
(кратно 100 мм). В разрезных сварных балках пролётом до 30 м принимается одно
уменьшение сечения поясов в каждую сторону от оси симметрии балки по длине (рис. 4).
При этом, согласно п. 5.19* [2], учитывать развитие пластических деформаций не
допускается.
Расчетные усилия в месте изменения сечения
M   0,5qx( L1  x) = 4053 кНм
Q  q(0,5L1  x) = 1146 кН
где x  L1 / 6 = 2,83 м
Требуемый момент сопротивления
 
Wmin
M
4053кНм
= 20731,5 см3

Rwy  c 195,5МПа 1
Требуемый момент инерции балки
  0,5Wmin
 h = 2073146 см4
I min
Требуемый момент инерции, приходящийся
на пояса
  I w = 1343007,6см4
I f ,min  I min
Требуемая площадь одного пояса
Af ,min 
2 I f ,min
h
2
f
Рис.4 Изменение сечения балки
= 69,2 см2
Требуемая ширина одного пояса
b f ,min 
Af ,min
tf
= 230 мм
Для назначения ширины измененного сечения пояса b f
проверим выполнение
следующих требований
b f  b f ,min = 230 мм

9

b f  0,1h = 200 мм

b f  180 мм

b f  0,5b f = 225 мм
b f = 250 мм
Площадь пояса измененного сечения
Af  b f t f = 75 см2
Момент инерции балки измененного сечения
I x  I w  0,5 Af h 2f = 2185475,9 см4
Момент сопротивления измененного сечения
Wx 
2 I x
= 21854,8 см3
h
Статический момент пояса относительно
нейтральной оси сечения балки
S f  0,5 Af h f = 7387,5 см3
Статический момент полусечения балки
  S f  S 0,5 w  S f 
S max
Рис.5 Место изменения
сечения балки
t w hw2
1,2  194 2
= 13032,9 см3
 7387,5 
8
8
Проверка прочности по максимальным растягивающим напряжениям по стыковому
шву нижнего пояса (точка А на рис.5)
 max 
M
 Rwy  c => 18,6  19,55 кН/см2
W x
Проверка прочности в месте изменения сечения по наибольшим приведенным
напряжениям на грани стенки (точка В) с учетом lос = 0
 пр   x2  3 yx2  18,04 2  3  3,232  18,9  1,15R y  c = 26,45 кН/см2
где  x 
 max hw
 yx 
h

18,6 194
= 18,04 – нормальное напряжение в срединной плоскости
200
стенки, параллельное оси балки
QS f
1146  7387,5

= 3,23 – касательное напряжение
I x t w 2185475,9 1,2
Проверка прочности опорного сечения на срез по максимальным касательным
напряжениям
 max 

Q1max S max
1718,38 13032,9

 8,54кН / м 2  Rs  c = 13,34 кН/см2
I x t w
2185475,9 1,2
Проверка прочности стенки балки на местное давление
 loc 
P
217,3

 8,8кН / м 2  R y  c = 23 кН/см2
t wlef 1,2  20,5
где P = qбнl = 38,8кН/м∙5,6м=217,3 кН– сосредоточенная нагрузка на главную балку от
второстепенных балок
lef = b+2tf = 205 мм – условная длина распределения нагрузки на стенку балки
b = 145 мм – ширина полки двутавра (балки настила)
qбн = 38,8 кН/м – расчетная погонная нагрузка на второстепенную балку
10
e.
Проверка общей устойчивости балки
Поскольку условия 1 
hf
bf
 6 (14,3<6) и 15 
bf
tf
 35 (1515<35) выполняются, то
можно воспользоваться следующей формулой

 l ef 
bf 
bf
    0,41  0,0032   0,73  0,016
tf 
tf

 b f 
 bf  E
 

h  R
y
 f

45 
45  45  2,6  10 5
 10,41  0,0032   0,73  0,016 
 17
3 
3  197 
230

где  = 1 – коэффициент при отсутствии пластических деформаций
 l ef

b f  b f
l ef

 => 2,44  17

Согласно выполнению данного условия устойчивость балок двутаврового сечения
обеспечивается и не требует дополнительной проверки
f.
Проверка местной устойчивости стенки балки
Условная гибкость стенки балки
w 
Ry
hw
tw
E
= 5,4
Поскольку  w > 3,2, то стенку балки с одной стороны необходимо укрепить
односторонним поперечным ребром жесткости
Расстояние между основными поперечными рёбрами a не должно превышать 2hw.
Допускается увеличивать указанное расстояние между рёбрами до значения 3hw при условии
проверки обеспечения местной устойчивости стенки по формуле (6.26) или (6.29) и общей
устойчивости балки по формуле
lef / b f   [0,35 + 0,0032
bf
tf
+ (0,76 - 0,02
bf bf
) ] E / Ry ,
t f hf
Ширина поперечного ребра жесткости
bh 
hw
 50 = 131 мм
24
Толщина поперечного ребра жесткости
t s  2bh
Ry
E
= 8,8 мм
Лист из широкополосной универсальной стали ts = 10 мм, bh = 150 мм
Рис.6 Расстановка ребер жесткости
11
Проверка первого отсека
Средние значения момента и поперечной силы в пределах отсека, действующих на
расстоянии x1 =2,7 м от опоры балки
qx1 ( L1  x1 ) 38,8  2,7(17  2,7)

= 749,03 кНм
2
2
L

 17

Q1ср  q 1  x1   38,8  2,7  = 225,04 кН
 2

2

M 1ср 
где q = 38,8 кН/м – расчетная нагрузка на 1 погонный метр балки настила
Среднее нормальное напряжение
1 
0,5M 1ср hw
Iw
= 9,95кН/см2
Среднее касательное напряжение
1 
Q1ср
t w hw
= 0,05 кН/см2
Устойчивость стенки балки при наличии местного напряжения и без учета
пластических деформаций
2
где  loc
 
 loc    
8,8   0,97 
 9,95

   



 
  0,95   c =1




25
,
7
15
,
97
5
,
6




cr
loc
,
cr
cr




P
217,3


 8,8кН / м 2
t wlef 1,2  20,5

 cr  10,31 
2
2
2
0,76  Rs

= 5,6 кН/см2
 2  ef2

a
3,8


= 1,96
hw 1,94
Ry
d
tw
ef 
E
= 5,4
d = 194 см – меньшая из сторон отсека
при а/ hw > 0,8 и отношении loc/ не более значений, указанных в табл. 8 прил. 2,
 cr 
ccr R y
w2
= 25,7 кН/см2, где
зависимости от значения параметра
 loc,cr 
c1 R y
a
tw
Ry
a 
 a2
E
коэффициент ссr принимается по табл. 6 прил. 2 в
b t
   f  f
hw  t w
3

25  3 
  0,8
   1,61 ,сcr = 32,6
194  1,2 

3
= 15,97 кН/см2, где с1 = 19,5
= 5,3
а =0,5a=1,9 м < 2hw – расстояние между основными поперечными ребрами
Проверка второго отсека
Средние значения момента и поперечной силы в пределах отсека, действующих на
расстоянии x2 = 8,2 м от опоры балки
12
M 2ср 
Q2ср
qx2 ( L1  x2 )
= 1399,9 кНм
2
L

 q 1  x 2  = 11,6 кН
 2

Среднее нормальное напряжение
2 
0,5M 2ср hw
Iw
= 18,6 кН/см2
Среднее касательное напряжение
2 
Q2 ср
t w hw
= 0,05 кН/см2
Устойчивость стенки балки при наличии местного напряжения и без учета
пластических деформаций
2
где  loc
 
 loc    
 18,6 8,8   0,05 

   



 
  1,28   c =1


 23,7 17,8   5,95 
 cr  loc,cr    cr 
P
217,3


 8,8кН / м 2
t wlef 1,2  20,5

 cr  10,31 


2
2
2
0,76  Rs

= 5,95 кН/см2
 2  ef2
a
3,3

= 1,7
hw 1,94
Ry
d
tw
ef 
E
= 5,4
d = 194 см – меньшая из сторон отсека
при а/ hw > 0,8 и отношении loc/ не более значений, указанных в табл. 8 прил. 2,
 cr 
ccr R y

2
w
= 23,7 кН/см2, где
коэффициент ссr принимается по табл. 6 прил. 2 в
3
зависимости от значения параметра
 loc,cr 
c1 R y
a
tw
Ry
a 
 a2
E
b t 
45  3 
   f  f   0,8
   2,9 ,сcr = 30
hw  t w 
194  1,2 
3
= 17,8 кН/см2, где с1 = 18,6
= 4,9
а =0,5a=1,75 м < 2hw – расстояние между основными поперечными ребрами
Вывод: увеличиваем толщину стенки или ставим продольные
ребра
13
g.
Расчет соединения поясов балки со стенкой
2

   c => 0,42  1

2

   c => 0,78  1

 1

  cr
  1
  
   cr
 2

  cr
  2
  
   cr
2
2
На основании выполнения данного условия соединение поясов составной балки со
стенкой осуществляется односторонним поясным швом
Расчетное усилие
N  T 2  V 2 = 1367 кН/м
Q1 max S f 1718,38 13032,9
где T 
= 1022,5 кН/м –

I x
2185475,9
усилие,
сдвигающее
пояс на единицу длины
V
P 217,7
=

lef 0,205
1062
кН/м
–
давление
от
второстепенной балки
Требуемый катет поясного шва определяется по
наибольшему значению
 при расчете по металлу шва
kf 

N
n f Rwf  wf  c
= 6,9 мм
Рис.8 Расчет поясных
швов
при расчете по металлу границы сплавления
kf 
N
n z Rwz  wz  c
= 7,3 мм
где n = 1 – при односторонней шве
f = 1,1 и z = 1,15 – коэффициенты, принимаемые для автоматической сварки в
положении в лодочку
Минимальное значение катета сварного шва (таблица 11) 8мм
Окончательно катет углового шва kf  1,2tw = 14 мм и принимается равным 8 мм
h. Расчет опорной части балки
Опорная реакция балки
F  Q1 max  Q2 max = 2527 кН
Требуемая площадь опорного
ребра из условия смятия торца ребра
Ap ,min 
F
2527
= 72,2 см2

R p c 35 1
Требуемая толщина опорного
ребра
t p ,min 
A p ,min
bp
= 29 мм
Рис.9 Опорная часть балки
где bp = 250 мм  b f – ширина опорного ребра
14
Момент инерции опорного ребра
Iy 
t p b 3p
12
= 3906 см4
где tp = 30 мм  tp,min – толщина опорного ребра
Площадь расчетного сечения, включающего сечение опорного ребра и примыкающей к
нему полосы стенки
A p  t p b p  t w bl = 103 см2
где bl  0,65t w
E
= 23,3 см – ширина полосы стенки
Ry
Радиус инерции
Iy
iy 
Ap
= 62 мм
Гибкость опорного ребра

l ef
iy
= 31,3
где lef = hw = 1940 мм – расчетная длина опорного ребра
Условная гибкость
 
Ry
E
= 3,3
Проверка устойчивости опорной части из плоскости балки как стойки, нагруженной
опорной реакцией
F
2527

 26,4  Ry c = 23 кН/см2
Ap 0,928 103
Вывод: условие не выполняется, увеличиваем толщину стенки
где  = 0,928 - коэффициент продольного прогиба
Проверка местной устойчивости опорного ребра
E
 t w => 250  1300 мм
Ry
b p  2t p (0,36  0,1 )
Катет шва, прикрепляющего опорное ребро к стенке, с учетом восприятия расчетного
усилия двумя швами и односторонней передачи усилия ( l w  85  f k f ), определяется по
наибольшему значению
kf 
kf 
F
= 11 мм
170  Rwf  wf  c
2
f
F
= 9,5 мм
170  f  z Rwz  wz  c
где  f = 0,8 и z = 1 – коэффициенты, принимаемые для полуавтоматической сварки в
вертикальном положении
Окончательно катет углового шва kf = 12 мм
Выступающая часть опорного ребра ap  1,5tp = 45 мм и принимается 20 мм
15
i.
Расчет и конструирование монтажного стыка балки
Изгибающий момент, воспринимаемый стенкой балки
Mw 
M I w 730303 730138,4
= 1591,83 кНм

Ix
3349745,9
где M” = M1max – расчетное усилие в месте расположения стыка
Расчетное усилие на один болт, воспринимаемое двумя поверхностями трения
соединяемых элементов
Qbh 
2 Rbh b Abn 
h
= 155 кН
где Rbh = 0,7Rbun = 77 кН/см2 – расчетное сопротивление растяжению высокопрочного болта
b = 1,0 – коэффициент условий работы соединения
Abn = 2,45 см2 – площадь сечения болта нетто(d=20 мм)
 = 0,42 – коэффициент трения
h = 1,02 – коэффициент надежности
Количество болтов в стыке поясов на полунакладке
n
где N f 
Nf
Qbh c
= 18,41=20
M   M w 7303,03  1591,83

= 2899 кН
hf
1,97
Суммарная площадь сечения накладок
Aн  b1н t н  2b2 н t н  A f => 150  135 см2
где tн = 18 мм – толщина листовой накладки
b1н = bf = 450 мм – ширина листовой полунакладки
b2 í  0,5(b f  t w )  (20....30) = 190 мм – ширина листовой накладки
Проверка ослабления накладок отверстиями под болты в середине стыка
Aп  Aн  2n1t н d o  0,85 A f => 121  115 см
где n1 = 4 – количество болтов в одном ряду
dо = d+2 = 22 мм – диаметр отверстия
Стык стенки перекрывается двумя вертикальными накладками из листа толщиной 8 или
10мм.
Расстояние между крайними по высоте рядами болтов
Рис.10 Монтажный стык балки
16
hmax  hw  2t н  2(a1 ..a2 ) = 1802 мм
Окончательно расстояние между крайними рядами болтов кратно a и принимается hmax
= 1800 мм
Число болтов в одном вертикальном ряду
nc 
hmax
 1 = 19
a
где a = 100 мм – расстояние между рядами болтов по вертикали
Сумма квадратов расстояний между парами симметрично расположенных болтов
2
= 114000 см2
hi2  h12  h22  ..  hmax

Проверка прочности стыка стенки по усилию, действующему на наиболее
нагруженные болты
N 
N
2
max
V
2
M h
  w max2
 m h
i

2
  Q  
 
  Qbh c => 134  155 кН
  nc m 

 
2
где m = 2 – число вертикальных рядов болтов с одной стороны стыка стенки
Q” = Q1max = 1718,38 кН – расчетное усилие в месте расположения стыка
17
6. Расчет и конструирование колонн
Расчетная схема. Расчетное усилие
a.
Геометрическая длина колонны
l c  hв н  t  hбн  hгб  a р  hф = 6783 мм
где hвн = 7800 мм – заданная отметка верха
настила
t = 12 мм – толщина настила
hбн = 270 мм – высота балки настила
hгб = 1600 мм – высота главной балки
пролета L1
aр  1,5tp – выступающая часть опорного
ребра главной балки
hф = 900 мм – заглубление подошвы
колонны ниже нулевой
отметки
Расчетная длина колонны
l ef  l c = 6783 мм
Рис.11 Определение расчетной
где  = 1 – коэффициент расчетной длины при
длины колонны
шарнирном закреплении колонны в
фундаменте
Расчетное усилие в стержне колонны
N  1,01F = 2037,8 кН
где 1,01 – коэффициент учитывающий собственный вес колонны
b. Подбор сечения колонны
Подбор сечения сплошной колонны
Условная гибкость колонны
 
Ry
E
= 2,9
где  = 80  [] = 120 - гибкость колонны
Требуемая площадь сечения
Amin 
N
= 118 см2
R y  c
где  = 0,641 - коэффициент продольного изгиба
центрально-сжатых элементов
Радиус инерции относительно оси y-y
i y ,min 
l ef

= 85 мм
Требуемая ширина полки
b f , min 
i y , min
2
= 354 мм
где 2 = 0,24 – коэффициент, зависящий от
размеров раскосной решетки
Ширина полки принимается в соответствии с
сортаментом bf = 360 мм
Требуемая толщина полки
Рис.12 Сечение сплошной
колонны
18
t f ,min 
0,5(b f  t w )
= 10 мм
E
(0,36  0,1 )
Ry
где tw = 12 мм – толщина стенки
Требуемая высота стенки
hw,min 
Amin  2b f t f
tw
= 383 мм
где tf = 10 мм  tf,min – толщина полки
Обеспечение местной устойчивости стенки двутаврового сечения
E
= 729 мм
Ry
hw  uwt w
где uw  1,2  0,35 = 2,2
Исходя из этих условий принимаем высоту стенки hw = 560 мм
Площадь сечения
A  2b f t f  hw t w = 139,2 см2
Момент инерции относительно оси y-y
Iy 
t f b 3f
= 7776 см4
6
Радиус инерции относительно оси y-y
Iy
iy 
A
= 75 мм
Радиус инерции относительно оси x-x
i x  0,43(hw  2t f ) = 267 мм
Гибкости колонны
y 
l ef
x 
l ef
iy
ix
= 90
= 25
Проверка общей устойчивости колонны относительно оси y-y

N
 R y  c => 25,9  27 кН/см2
A
где  = 0,565 – коэффициент продольного изгиба центрально-сжатых элементов
Недонапряжение
 
Ry  
Ry
100% = 4,1% < 5%
Подбор сечения сквозной колонны
Требуемая площадь сечения
Ab,min 
N
= 96 см2
R y  c
где  = 0,785 – коэффициент продольного изгиба центрально-сжатых элементов
Требуемый радиус инерции относительно материальной оси x-x
19
i x ,min 
l ef

= 113 мм
где  = 60  120 – гибкость колонны
№30а II,y = 436 см4, ix = 12,5 см, iI,y = 2,95 см,
A = 49,9 см2, bI = 145 мм, hI = 300 мм
Гибкость стержня относительно оси x-x
x 
l ef
ix
= 54
Проверка
устойчивости
относительно оси x-x

колонны
N
 R y  c => 24,4  27 кН/см2
 x Ab
где x = 0,836 – коэффициент продольного
изгиба центрально-сжатых
элементов
Ab = 2A = 99,8 см2 – площадь сечения
колонны
Недонапряжение
 
Ry  
Ry
100% = 9,6% < 5%
Данное недонапряжение невозможно
уменьшить в пределах сортамента прокатных
профилей
Требуемая
гибкость
относительно
свободной оси y-y
 y ,min  2y ,ef  12  2x  12 = 36
Рис.13 Сечение сквозной колонны
где 1 = 40 – гибкость отдельной ветви колонны на свободном участке между планками при
изгибе ее в плоскости, перпендикулярной оси 1-1
Требуемый радиус инерции
i y ,min 
l ef
 y ,min
= 188 мм
Требуемая ширина сечения колонны
bmin 
i y ,min
2
= 362 мм
где 2 = 0,52 – коэффициент, зависящий от размеров раскосной решетки для двух
Ширина колонны кратна 50 мм и принимается b = 400 мм, обеспечивая необходимый
зазор b’ между полками ветвей (b  bI+100)
Расчетная длина ветви в сварной колонне
l в  1i I , y = 1180 мм
Ширина планок bs = 0,8b = 320 мм при условии, что расстояние между центрами
тяжести планок по длине колонны кратно 100 мм (l = lв+bs = 1500 мм)
Толщина планок принимается ts = 0,06bs = 20 мм
Момент инерции планки относительно собственной оси x’-x’
Is 
t s bs3
= 5461,3 см4
12
Момент инерции сечения относительно свободной оси y-y
I y  2[ I I , y  A(0,5b  z 0 ) 2 ] = 39505 см4
где z0 = 0,325 см – расстояние от оси y-y до наружной грани стенки
20
Радиус инерции сечения относительно оси y-y
Iy
iy 
Ab
= 199 мм
Гибкость стержня относительно оси y-y
y 
l ef
iy
= 34
Расстояние между осями ветвей колонны
b0  b  2z 0 = 394 мм
Поскольку
I sl
 5 => 48  5, то приведенная гибкость стержня относительно оси yI I , y b0
y
 y ,ef  2y  12 = 53
Проверка устойчивости колонны относительно свободной оси y-y

N
 R y  c => 24,4  27 кН/см2
 ef Ab
где ef = 0,836 – коэффициент продольного изгиба
Выбор типа сечения колонны
Для дальнейшего расчета принимаем колонну сквозного сечения
c.
Расчет планок
Условная поперечная сила
Q fic

E 
7,15 *10 6  2330 
N

R y 

= 27,3 кН

 ef
Условная поперечная сила, приходящаяся на планку
одной грани
Qs  0,5Q fic = 13,7 кН
Сила, срезывающая планку
Fпл 
Qs l
= 52,2 кН
b0
Рис.14 Крепление планки
Момент, изгибающий планку в ее плоскости
M пл 
Qs l
= 1027,5 кНсм
2
Момент сопротивления поперечного сечения планки
Ws 
t s bs2
= 341 см3
6
Проверка напряжения в планке от изгиба

M пл
 R y  c => 3  27 кН/см2
Ws
Катет шва, прикрепляющего планку к ветвям колонны, определяется по наибольшему
значению
21
kf 
kf 
36M пл2  Fпл2 l w2
 f l w2 Rwf  wf  c
36M пл2  Fпл2 l w2
 z l w2 Rwz  wz  c
= 5 мм
= 4 мм
где  f = 0,7 и z = 1 – коэффициенты, принимаемые для полуавтоматической сварки
lw = bs-10 = 310 мм – расчетная длина углового шва при наличии только вертикальных
швов
Окончательно катет шва kf = 6 мм
d. Расчет оголовка колонны
Конструктивные размеры опорной плиты
bpl = b+30 мм
lpl = hI+30 мм
(43033025)
tpl = 20..25 мм
Длина сминаемой поверхности
l r  b p  2t pl = 350 мм
где bp = 240 мм – ширина опорного ребра главной
балки
tpl = 25 мм – толщина опорной плиты
Требуемая толщина ребра оголовка
t r ,min 
F
= 16 мм
l r R p c
Требуемая
длина
сварных
швов,
прикрепляющих ребро оголовка к ветвям колонны
 при расчете по металлу шва
l w,min 
F
= 190 мм
4  f k f Rwf  wf  c
 при расчете по металлу границы сплавления
l w,min 
F
= 155 мм
4  z k f Rwz  wz  c
где  f = 0,7 и z 1 = – коэффициенты, принимаемые
для полуавтоматической сварки
kf  1,2tmin = 19,2 мм – катет шва (19 мм)
Рис.15 Оголовок колонны
tmin = tr – наименьшая из толщин соединяемых
элементов
Высота ребра оголовка принимается равной 420 мм из условия lw,min  hr  lw,max, где
lw,max = 85 fkf = 1130,5 мм – наибольшая длина флангового шва
Проверка ребра оголовка на срез

F
 Rs  c => 15  15,66 кН/см2
2hr t r
e.
Расчет базы колонны
Требуемая площадь опорной плиты из условия смятия бетона под плитой
Apl ,min 
N
= 3341 см2
Rb,loc
где Rb,loc = 1,5Rbb9 = 6,1 МПа – расчетное сопротивление бетона при местном сжатии
Rb = 4,5 МПа – расчетное сопротивление сжатию бетона
22
b9 = 0,9 – коэффициент условий работы бетона
Ширина плиты
B pl  hI  2t s  2c = 43 см
где ts = 15 мм – толщина траверсы
c = 50 мм – свес плиты
Требуемая длина плиты
A pl ,min
L pl ,min 
B pl
= 77,7 см
Длина плиты кратна 10 мм и
принимается Lpl = b+2b1 = 780 мм,
где b1 = 190 мм  50 мм – свес плиты
Размеры фундамента в плане
Lf = Lpl+20 см
(980630)
Bf = Bpl+20 см
Площадь
опорной плиты
A pl  L pl B pl = 3354 см2
Работа опорной плиты
изгиб от равномерной нагрузки
b 
на
N
= 0,6 кН/см2
Apl
Площадь
фундамента
верхнего
обреза
A f  L f B f = 6174 см2
Рис.16 База колонны
Проверка условия прочности фундамента
Rb,loc  Rb
Af
Apl
  b => 0,61  0,6 кН/см2
где  = 1 – для бетона класса ниже В25
Изгибающие моменты, действующие на полосе шириной d = 1 см
 при опирании на три канта (участок 1)
M   b a 2 = 40 кН
где  = 0,074 – коэффициент для расчета на изгиб плит, опертых на три или два канта
a = hI = 300 мм – расстояние между кромками ветвей траверсы
 при опрании на четыре канта (участок 2)
M   b a 2 = 37 кН
где  = 0,069 – коэффициент, зависящий от отношения более длинной стороны к более
короткой (b2/a = 1,29)
 на консольном участке (участок 3)
M  0,5 b c 2 = 7,5 кН
Требуемый момент сопротивления полочки плиты
Wd ,min 
M max
= 1,5 см3
R y c
где Mmax = 40 кН – наибольший изгибающий момент, действующий на полосе
Требуемая толщина плиты
t pl ,min  6Wd ,min = 30 мм
Толщина плиты назначается tpl = 30 мм
Требуемая длина сварных швов, через которые передается усилие стержня колонны на
траверсу
23
 при расчете по металлу шва
l w,min 
N
= 243 мм
n f k f Rwf  wf  c
 при расчете по металлу границы сплавления
l w,min 
N
= 199 мм
n z k f Rwz  wz  c
где n = 4 – число учитываемых швов, которые удобно варить
f = 0,7 и z = 1 – коэффициенты, принимаемые для полуавтоматической сварки
kf  1,2ts = 18 мм – катет шва (15 мм)
Высота траверсы принимается равной 500 мм из условия lw,min  hs  lw,max, где lw,max =
85 fkf = 893 мм – наибольшая длина флангового шва
Требуемый катет шва, прикрепляющего ветви траверсы к опорной плите
полуавтоматической сваркой
N
= 6 мм
 lw  f Rwf  wf  c
N
= 5 мм

 lw  z Rwz  wz  c
k f ,min 
k f ,min
где lw = 2[(Lpl-1)+2(b1-1)] = 226 см – суммарная длина швов с учетом на непровар
Окончательно катет шва принимается kf = 8 мм
Приварка торца колонны к плите выполняется конструктивными швами kf = 7 мм
Диаметр анкерных болтов при шарнирном сопряжении конструктивно принимается 20
мм
24