x = 3

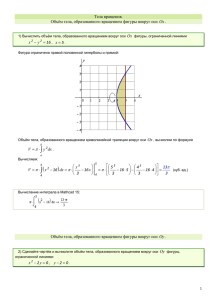
Контрольная работа
по дисциплине «Элементы высшей математики»
Специальность: «Программирование в компьютерных системах»
1 курс
2 семестр
1. Вычислить следующие неопределенные интегралы.
3. Вычислите площади фигур, ограниченных указанными
1) x – y + 2=0, y=0, x = –1 и x =2;
2) 2x - 3y +6 = 0, y = 0 и x =3;
3) x – y + 3 = 0, x + y – 1=0 и y =0;
линями:
4) x – 2y + 4 = 0, x +2y – 8 =0, y = 0, x=-1 и x =6;
5) y= 𝑥 2 , y=0, x=0 и x=3;
6) y= 3𝑥 2 , y=0, y =0, x= -3, и x=2;
7) y =𝑥 2 +1, y =0, x = -1 и x =2;
8)y= 0.52 +2, y =0, x= 1 и x = 3;
9) y = - (1/3)𝑥 2 +3, y =0, x =0 и x =3;
10) y =1/x, y =0, x =1 и x =3.
4. Найти объём тел и пути движения.
1. Найти объём тел, образованных вращением вращением вокруг оси Ох
фигур, ограниченных линиями: y 2 = (x – 1)3 и прямой x = 2.
2. Найти объём тел, образованных вращением вращением вокруг оси Ох
фигур, ограниченных линиями: y =
64
x2 +16
, x 2 = 8y.
3. Найти объём тел, образованных вращением вращением вокруг оси Ох
фигур, ограниченных линиями: 𝑦 2 = 𝑥, 𝑥 2 = 𝑦.
4. Найти объём тел, образованных вращением вращением вокруг оси Ох
фигур, ограниченных линиями: 𝑦 = √𝑥𝑒 𝑥 , 𝑥 = 1, 𝑦 = 0.
5. Найти объём тел, образованных вращением вращением вокруг оси Ох
фигур, ограниченных линиями: 𝑦 =
𝑥2
2
,𝑦 =
𝑥3
8
.
6. Найти объём тела, образования вращением вокруг оси Ох плоской фигуры,
ограниченной линиями
𝑥2
𝑦2
𝑎
𝑏2
+
2
= 1, 𝑦 = 0 и расположенной в квадратах I и II.
7. Найдите объём тела, образованного вращением вокруг оси Ох плоской
фигуры , ограниченной линиями
квадратах I и II.
𝑥2
𝑦2
𝑎
𝑏2
+
2
= 1, 𝑦 = 0 и расположенной в
8. Найдите объём тела, полученного вращением вокруг оси Ох плоской
фигуры, ограниченной полуволной синусоиды 𝑦 = sin 𝑥 (0 ≤ 𝑥 ≤ 𝜋) и осью
Ох.
9. Найдите путь, пройденный точкой за четвёртую секунду, зная скорость ее
прямолинейного движения 𝑣 = 3𝑡 2 − 2𝑡 − 3 (м/с).
10. Найдите путь, пройденный точкой от начала движения до ее остановки,
зная скорость ее прямолинейного движения 𝑣 = 18𝑡 − 6𝑡 2 (м/с).
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Кремер И.Ш. и др. Высшая математика для экономистов. М.: «Банки и биржи», «ЮНИТИ»,
1997.
2. Малыхин В.И. Математика в экономике. М.: ИНФРАМ, 2000.
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1986.
4. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических
вузов. М.: Высшая школа, 1982,ч.1,2.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.:
Высшая школа, 1980, ч.1,2.
6. Кузнецов А.В., Кузнецова Д.С. и др. Сборник задач и упражнений по высшей
математике. Минск: Высшая школа, 1994.
9. Справочник по математике для экономистов. Под ред. Ермакова. М.: Высшая школа, 1987.