Обзорная лекция на тему Многокритериальные задачи

§3. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
ПРИНЯТИЯ РЕШЕНИЙ
1. Математическая модель многокритериальной ЗПР
Пусть D – произвольное множество, элементы которого называются допустимыми решениями
или альтернативами, а f1, …,fm – числовые функции (целевые функции, критерии), заданные на множестве D. Требуется найти оптимальное решение из множества D, максимизирующее функции
f1 ,..., f m на множестве D:
f ( x)  ( f 1 ( x),..., f m ( x))  max,
x  D.
(1)
Здесь f(x) –- m-вектор-функция аргумента x  D , D  Rn .
Пример
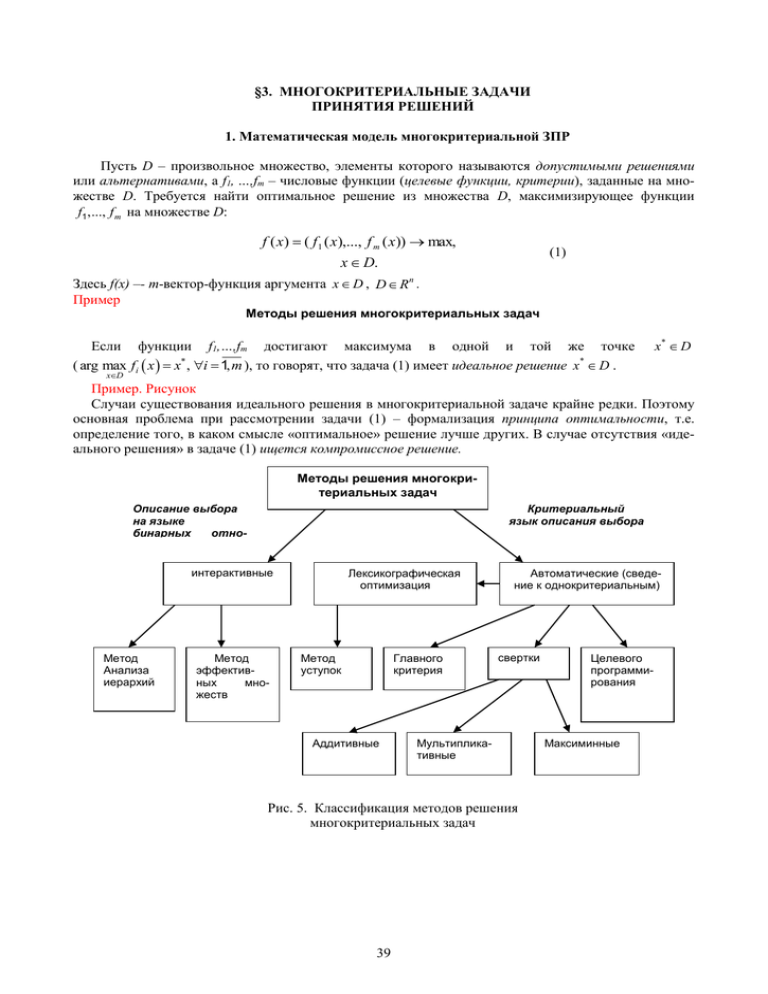
Методы решения многокритериальных задач
Если функции f1,…,fm достигают максимума в одной и той же точке
( arg max fi  x   x* , i  1, m ), то говорят, что задача (1) имеет идеальное решение x*  D .
x*  D
xD
Пример. Рисунок
Случаи существования идеального решения в многокритериальной задаче крайне редки. Поэтому
основная проблема при рассмотрении задачи (1) – формализация принципа оптимальности, т.е.
определение того, в каком смысле «оптимальное» решение лучше других. В случае отсутствия «идеального решения» в задаче (1) ищется компромиссное решение.
Методы решения многокритериальных задач
Описание выбора
на языке
бинарных
отношений
Критериальный
язык описания выбора
интерактивные
Метод
Анализа
иерархий
Метод
эффективных
множеств
Лексикографическая
оптимизация
Метод
уступок
Главного
критерия
Аддитивные
Автоматические (сведение к однокритериальным)
свертки
Мультипликативные
Рис. 5. Классификация методов решения
многокритериальных задач
39
Целевого
программирования
Максиминные
2. Метод эффективных множеств
Пусть Yi - множество значений функции f i , т.е. множество всех оценок по i -му критерию
m
( i  1, m ). Тогда множество Y   Yi  R m , состоящее из всевозможных упорядоченных наборов оцеi 1
нок по критериям 1,…,m, называется множеством векторных оценок. Любой элемент y  Y представляет собой вектор y   y1,
всем критериям, т.е. набор
, ym  , где yi  Yi . Для всякой альтернативы x  D набор ее оценок по
 f1  x  ,
, f m  x   есть векторная оценка альтернативы x . Векторная
оценка альтернативы содержит полную информацию о ценности (полезности) этой альтернативы для
ЛПР и сравнение любых двух исходов заменяется сравнением их векторных оценок.
Пример.
 
 
Пусть x1  D и x 2  D - две такие альтернативы, что fi x1  f i x 2 , i  1, m (сравнимые альтер1
нативы). В этом случае понятно, что альтернатива x не хуже, чем x 2 . (рис.) Предположим при этом,
 
 
что существует такое i0  1, m , что fi0 x1  f i0 x 2 . Тогда альтернатива x1 лучше чем x 2 . (рис.) Если
относительно пары альтернатив нельзя сказать, какая из них лучше, то их называют несравнимыми
(рис).
Определение 1. Говорят, что альтернатива x1  D доминирует (по Парето) альтернативу
P
x 2  D , (будем обозначать x1 x 2 ) если
fi ( x1 )  fi ( x2 ), i  1, m ,
и  i0 , i0  {1, m} , такое, что
fi0 ( x1)  fi0 ( x2 ) .
Точка x*  D называется оптимальной по Парето (эффективной), если не существует x  D ,
доминирующей x* .
Обозначим DC  D область согласия, которая не содержит недоминируемых точек (любая точка из Dc может быть улучшена). Эффективная область (множество Парето) Dэ D содержит все
оптимальные по Парето точки.
 
Образ множества D Э в пространстве критериев R m обозначим Y Э . Множество Y Э  f D Э
называется множеством эффективных оценок (множеством Парето в пространстве критериев).
РИСУНОК
Оптимальные решения многокритериальной задачи следует искать только среди элементов множества альтернатив D Э . В этой области ни один критерий не может быть улучшен без ухудшения
хотя бы одного из других. Важным свойством множества Парето D Э является возможность «выбраковывать» из множества альтернатив D заведомо неудачные, уступающие другим по всем критериям. Обычно решение многокритериальной задачи должно начинаться с выделения множества D Э .
При отсутствии дополнительной информации о системе предпочтений ЛПР большего сделать нельзя.
3. Построение эффективной области в случае двух линейных критериев (m=2)
Пример Математическая модель задачи имеет вид:
f ( x, y)  ( f1 ( x, y)  2x  y, f 2 ( x, y)  2x  3 y)  max ,
D  {( x, y) : x 2  y 2  100, x  0, y  0} .
Изобразим геометрически допустимую область D, определяемую ограничениями задачи, и
найдем точки, оптимальные по критериям f1(x,y) и f2(x,y) в отдельности (точки a и b на рис.1) + ЧЕрноруцкий 49
40
y
10
a
grad f1
z=c
b
grad f2
x
Рис.1
Проверим произвольную точку zD на Парето-оптимальность. Через неё проведём линии
уровня целевых функций и рассмотрим конус K  z  , образованный пересечением полуплоскостей,
ограниченных этими линиями и лежащих в направлении увеличения соответствующих целевых
функций (конус доминирования для альтернативы z ) (на рис. 1 этот конус заштрихован).
Геометрически ясно, что точка z=(x,y) Dэ тогда и только тогда, когда во внутреннюю часть конуса доминирования не попадает ни одна точка из D (т.е.  K  z   D  z ) (на рис. 1, например, это
точка z=a). Точка z=c Dэ (рис. 1), т.к. заштрихованный конус с вершиной в точке c имеет непустое
пересечение с областью D  K  z  \ z  D   (все точки этого пересечения улучшают точку c).
Т.о. эффективные точки лежат только между точками оптимума, полученными при решении
многокритериальной задачи отдельно по каждому из критериев, и в случае выпуклой области D множество Dэ – вся часть выпуклой оболочки между этими точками.
Теорема Карлина. Пусть множество векторных оценок Y строго выпукло, ограничено и замкнуто. Для того чтобы альтернатива x*  D была Парето-оптимальна, необходимо и достаточно, чтобы
существовали такие неотрицательные коэффициенты 1  0,
m
, m  0,  i  1 , для которых
i 1
i fi  x*   i fi  x  , x  D .
m
m
i 1
i 1
Ограниченность и замкнутость множества векторных оценок предполагаются для того, чтобы
m
можно было гарантировать существование Парето-оптимальных альтернатив. Условие   i  1 доi 1
бавляется для того, чтобы избежать тривиального случая 1 
 m  0 .
Э
Доказательство. Необходимость. Пусть x  D . Тогда пересечение конуса доминирования
*
  со множеством векторных оценок
 K  x  \ x  D   (рис. )
K x*
*
 
Y состоит из единственной векторной оценки f x* :
*
41
Рис.
Из теоремы об отделимости выпуклых множеств следует, что существует такая гиперплоскость
 m

Г   f : i fi    в пространстве векторных оценок R m , которая проходит через точку f x* :
 i 1

 
  i f i  x*    ,
m
(1*)
i 1
так, что множество Y целиком лежит в одном из полупространств, порождаемых этой гиперплоскостью:
m
i fi  x    , f  x   Y ,
(2*)
i 1
 
а конус K x* - в другом:
 i ki  x    , k  x*   K  x*  .
m
(3*)
i 1
Из (1*) и (2*) следует, что
i fi  x*   i fi  x , f  x   Y ,
m
m
i 1
i 1
m
т.е. в точке x* линейная функция критериев   i fi  x  действительно достигает максимума.
i 1
Установим неотрицательность коэффициентов 1 ,
,  m . Из (1*) и (3*) получаем:
i  ki  x   fi  x*    0, k  x*   K  x*  .
m
 
i 1
 
Полагая ki  x   fi x , i  j , ki  x   f i x*   , где   0 , для некоторого номера j имеем
*
 j  0 . В силу произвольности выбора номера j получаем i  0, i  1, m . Необходимость теоремы доказана.
Достаточность. Пусть предположение теоремы выполняется в точке x* при положительных
1 , , m , но x*  D Э . Тогда существует альтернатива x , доминирующая x* по Парето, т.е.
 
fi  x   f i x* , где хотя бы одно неравенство строгое. Но тогда
  i f i  x      i f i  x*  ,
m
m
i 1
i 1
что приводит к противоречию.
Предположим теперь, что предположение теоремы выполняется в точке x* , причем некоторый
коэффициент, например 1 , равен нулю. Если x*  D Э , то существует альтернатива x , доминирую-
42
 
щая x* по Парето, т.е. fi  x   f i x* , где хотя бы одно неравенство строгое. На самом деле
 
m
m
i 1
i 1
 
fi  x   fi x* , i  2, m , поскольку если это не так, то  i fi  x    i fi x* , что противоречит ис-
 
ходному предположению. Следовательно, f1  x   f1 x* .
 
Рассмотрим векторную оценку f  x  , лежащую на отрезке, соединяющем f1  x и f1 x* :
 
f  x    f  x   1    f x , 0    1 .
*
С одной стороны,
  i f i  x     i f i  x      i f i  x*  .
m
m
m
i 1
i 1
i 1
С другой стороны, из предположения о строгой выпуклости множество векторных оценок вытекает, что f  x  принадлежит внутренности Y . Но ни одна точка, принадлежащая внутренности выпуклого множества, не может максимизировать линейную функцию координат. Полученное противоречие доказывает достаточность условий теоремы и теорему полностью.
В векторной оптимизации кроме множества Парето в общем случае нет общих правил, по которому варианту x1 отдается предпочтение по сравнению с другим вариантом x2.
Часто решение многокритериальной задачи состоит в построении множества Паретооптимальных точек и дальнейшем выборе одной из них на основе «здравого смысла» или с помощью
какого-либо другого критерия.
В этой ситуации говорят, что для каждой задачи векторной оптимизации должно существовать
так называемое лицо, принимающее решение (ЛПР), которое либо формулирует правило, по которому
следует отдавать предпочтение (приоритет) одним вариантам по сравнению с другими, либо непосредственно определяет выбор между вариантами.
Во всех случаях задача многокритериальной оптимизации каким-то способом сводится к задаче с одним критерием. Существует много способов построения такого окончательного критерия,
однако ни одному из них нельзя заранее отдать наибольшее предпочтение. Для каждой задачи этот
выбор должен делаться лицом, принимающим решение.
4. Нормирование критериев
При решении многокритериальной задачи часто возникает проблема нормирования – приведения критериев к единому масштабу и безразмерному виду.
Наиболее часто используется замена абсолютных значений критериев их :
1) безразмерными относительными величинами:
f k ( x) 
f k ( x)
*
, f k  max f k ( x) ;
*
xD
fk
2) относительными значениями отклонений от оптимальных значений критериев f*k
5. Метод аддитивной свертки критериев.
Пусть критерии соизмеримы (например, нормированы) и определен вектор весовых коэффициентов критериев =(1,…,m), характеризующих важность соответствующего критерия (если fi f j ,
то  i   j ):
m

i 1
i
 1,  i  0, i  1, m .
Решается задача оптимизации скалярного критерия:
43
m
F ( x)   i f i ( x)  max, x D .
(1*)
i 1
Из теоремы Карлина следует, что решение задачи (1*) эффективно для задачи (1).
Пример
6. Метод главного критерия
Все целевые функции, кроме одной (главной), переводятся в разряд ограничений. Пусть
  ( 2 ,  3 ,...,  m ) – вектор, компоненты которого – нижние границы соответствующих критериев.
Оптимальным считается решение, при котором критерий f1 достигает своего максимального значения при условии, что по всем остальным критериям достигнуты значения, не меньше заданных.
Практическая процедура назначения пороговых значений – Подиновский, Ногин_47
Задача будет иметь вид:
F ( x )  f1 ( x ) 
 max
f i ( x )   i , i  2, m,
x  D.
Полученное этим методом решение может не быть эффективным.
Пример 5.
7. Метод последовательных уступок.
1. Критерии нумеруются в порядке убывания их важности.
2. Определяется значение f 1*  max f 1 ( x) . Лицом, принимающим решение, устанавливается велиxD
чина уступки 1 по этому критерию.
3. Решается задача:
(А)
f 2 ( x )  max, x  D, f1 ( x)  f1*  1.
Далее пункты 2 и 3 повторяются для критериев f 2 ,..., f m . Получаемое решение не всегда является эффективным.Пример 6.
8. Метод целевого программирования
Оптимальным считается решение, дающее наиболее близкое (в некоторой метрике) приближе-
~
ние значения каждого критерия к определенной (целевой) величине f k – идеальной точке. Пусть
~
~
~
f  ( f1 ,..., f m )
m
w
i
–
вектор
целевых
значений,
w  ( w1 ,..., wm ) -
вектор
весов,
обычно
 1, wi  0, i  1, m . Тогда задача целевого программирования имеет вид:
i 1
m
~
~
d ( f ( x ), f )   ( wi | f i ( x )  f i | p )1 / p  min, x  D ,
i 1
~
где d () - расстояние (мера отклонения) f ( x ) от f , 1  p   .
Пример
9. Метод, использующий
принцип гарантированного результата
метод максиминной свертки
*
Пусть f i , i  1, m , – оптимальные значения на D каждого из критериев в отдельности или некоторая система нормативов (контрольных показателей). Оптимальным считается решение, которое
максимизирует наихудшее значение отношения реально достигнутого показателя f i к его контрольному значению f i * :
44
f i ( x)

 max, x  D.
i
f i*
f ( x)
f ( x)
Обозначим   min i * . Очевидно,   i *  0 .
i
fi
fi
min
 -задача:

 max,

f i ( x)
f i*
 0,
x  D.

Получаемое решение эффективно. Оптимальное значение   max  , 0    1 . Чем меньше
 , тем противоречивее
критерии. Пример
45