Нахождение основания систем счисления

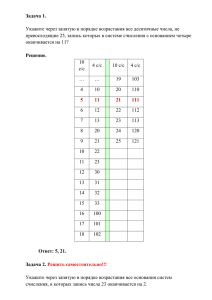
Нахождение основания систем счисления
В заключение изучения темы «Системы счисления»
рассмотрим задачи на нахождение основания систем счисления.
Такие задачи в обязательном порядке присутствуют на экзамене.
В домашних заданиях присутствовали такие задачи в качестве
задач повышенной трудности. Повышенной трудности эти задачи
считались только потому, что мы ещё не изучили алгоритма
решения таких задач. Но уже с помощью пройденного материала
вы уже могли попробовать сообразить, как их решить, хотя бы
простым подбором.
На этом уроке мы рассмотрим алгоритм решения таких задач.
Обычно задачи на нахождение основания систем счисления
сводятся к задачам всего двух видов:
1. В системе счисления с некоторым основанием число ____
записывается в виде _______. Укажите это основание.
2. Укажите через запятую в порядке возрастания все основания
систем счисления, в которых запись десятичного числа _____
оканчивается на ______.
Решение задач первого типа сводится к решению очень
простенького квадратного уравнения.
Решение задач второго типа сводится к нахождению делителей.
числа, получаемого как разность между заданным числом и
заданным окончанием
Звучит немного сложно, а на деле очень просто.
Рассмотрим на примерах.
1
Задача из Д/З. В системе счисления с некоторым основанием число
43 записывается в виде 133. Укажите это основание.
Вспомним, как мы переводим число из десятичной системы счисления в
любую другую.
Мы делим целую часть числа на основание системы счисления.
Обозначим искомое основание Х, а результат деления R.
43
Х
X*R
R
-
3
-
X
X*1 1
3
43 – X * R = 3
X * R = 40
R – X*1 = 3
R=X+3
X * ( X + 3 ) = 40
X 2 + 3X – 40 = 0
D = b2 – 4ac = 169 = 132
X1= (-3 + 13)/2 = 5
X2 = (-3 – 13)/2 = - 8
Ответ: 5.
Легко себя проверить
-
43
5
40
8
3
-
5
5
1
3
2
Потренируемся.
Задача . В системе счисления с некоторым основанием число 38
записывается в виде 102. Укажите это основание.
38
Х
X*R
R
-
2
-
X
X*1 1
0
38 – X * R = 2
X * R = 36
R – X*1 = 0
R=X
X * X =36
X=6
Ответ: 6.
Проверяем себя
-
38
6
36
6
2
-
6
5
1
0
3
Решение задач второго типа сводится к нахождению делителей. числа,
получаемого как разность между заданным числом и заданным окончанием.
Звучит сложно, но на примере видно, что совсем просто.
Задача из Д/З. Укажите через запятую в порядке возрастания все
основания систем счисления, в которых запись
десятичного числа 36 оканчивается на 4.
Вспомним, как мы переводим число из десятичной системы счисления в
любую другую.
Мы делим целую часть числа на основание системы счисления.
36
X
X*R
R
4
36 – X * R = 4
X * R = 32
32 / X = R
Задача сводится к нахождению делителей числа 32.
Это будут: 1, 2, 4, 8, 16, 32.
Т.к. число заканчивается на 4, значит основание СС > 4
Ответ: 8, 16, 32.
4
Потренируемся.
Задача. Укажите через запятую в порядке возрастания все
основания систем счисления, в которых запись
десятичного числа 51 оканчивается на 3.
51
X
X*R
R
3
51 – X * R = 3
X * R = 48
48 / X = R
Задача сводится к нахождению делителей числа 48.
Это будут: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
Т.к. число заканчивается на 3, значит основание СС > 3
Ответ: 4, 6, 8, 12, 16, 24, 48.
5