109. Спектральные закономерности В середине XVIII в. Г

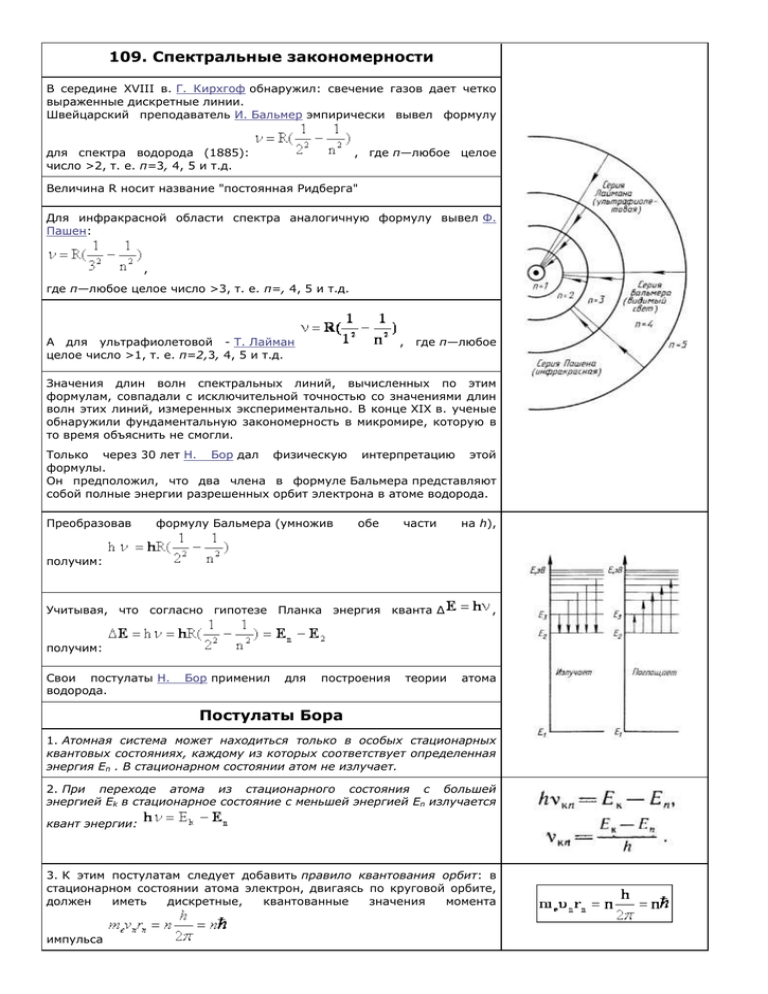
109. Спектральные закономерности
В середине XVIII в. Г. Кирхгоф обнаружил: свечение газов дает четко
выраженные дискретные линии.
Швейцарский преподаватель И. Бальмер эмпирически вывел формулу
для спектра водорода (1885):
число >2, т. е. п=3, 4, 5 и т.д.
, где п—любое целое
Величина R носит название "постоянная Ридберга"
Для инфракрасной области спектра аналогичную формулу вывел Ф.
Пашен:
,
где п—любое целое число >3, т. е. п=, 4, 5 и т.д.
А для ультрафиолетовой - Т. Лайман
целое число >1, т. е. п=2,3, 4, 5 и т.д.
,
где п—любое
Значения длин волн спектральных линий, вычисленных по этим
формулам, совпадали с исключительной точностью со значениями длин
волн этих линий, измеренных экспериментально. В конце XIX в. ученые
обнаружили фундаментальную закономерность в микромире, которую в
то время объяснить не смогли.
Только через 30 лет Н. Бор дал физическую интерпретацию этой
формулы.
Он предположил, что два члена в формуле Бальмера представляют
собой полные энергии разрешенных орбит электрона в атоме водорода.
Преобразовав
формулу Бальмера (умножив
обе
части
на h),
получим:
Учитывая, что согласно гипотезе Планка энергия кванта Δ
,
получим:
Свои постулаты Н.
водорода.
Бор применил
для
построения
теории
атома
Постулаты Бора
1. Атомная система может находиться только в особых стационарных
квантовых состояниях, каждому из которых соответствует определенная
энергия Еn . В стационарном состоянии атом не излучает.
2. При переходе атома из стационарного состояния с большей
энергией Ek в стационарное состояние с меньшей энергией En излучается
квант энергии:
3. К этим постулатам следует добавить правило квантования орбит: в
стационарном состоянии атома электрон, двигаясь по круговой орбите,
должен
иметь
дискретные,
квантованные
значения
момента
импульса
где rn радиус n-ой
орбиты; vn—скорость
электрона
на
этой
орбите; me— масса электрона, п—целое число - номер орбиты или
главное квантовое число.
Модель атома водорода по Бору
На электрон со стороны ядра действует кулоновская сила, сообщая ему
центростремительное ускорение. Поэтому
Из правила квантования:
Подставляя уравнение для скорости электрона на орбите в предыдущее,
получим:
, где n=1,2,3...
Если п=1, а r1 =0,5-10-10 м, то r2=r1.n2=4r1, r3=9r1 и т.д.
Т.о.
или rn~n2.
Полная энергия атома равна:
Подставляя
выражение
Е = Ek + Eп
для
радиуса
стационарной
орбиты,
получим:
Знак "-" говорит о том, что между электроном и ядром действуют силы
притяжения.
Переход электрона с более высокой орбиты k на
провождается излучением фотона с частотой:
орбиту п со-
Таким образом, мы пришли к формуле Бальмера,
где
- постоянная Ридберга.
Трудности теории Бора
Правило квантования Бора применимо не всегда, представление об
определенных орбитах, по которым движется электрон в атоме Бора,
оказалось условным. Теория Бора неприменима для многоэлектронных
атомов и не объясняет ряд спектральных закономерностей.
В 1917 г. А. Эйнштейн предсказал возможность перехода атома с
высшего энергетического состояния в низшее под влиянием внешнего
воздействия.
Такое
излучение
называется вынужденным
излучением и лежит в основе работы лазеров.