Своеобразие и значение учебной деятельности ... изменяет сам себя. Эльконин Д.Б.

Своеобразие и значение учебной деятельности в том, что ребенок
изменяет сам себя.
Эльконин Д.Б.
Как вести работу так, чтобы не причинить вреда ребенку, укрепить в
нем веру в свои силы, интерес к содержанию учебного процесса? Для
организации
эффективного хода формирования учебной деятельности
учителю важно видеть каждого ученика
на всех этапах работы.
Иными словами, необходимо организовывать такое образование, которое
имеет развивающий характер.
Осуществив три выпуска по программе развивающего
обучения
системы Д.Б. Эльконина—В.В.Давыдова смеем утверждать, что способности
ребенка к точным наукам обнаруживаются очень рано — значительно
раньше, чем другие стороны интеллектуальной одаренности.
Одной из форм организации свободного времени учащихся и составной
частью учебно-воспитательного процесса в школе является внеклассная
работа. Математический кружок наиболее оптимальное занятие
для
формирования стохастических понятий.
Под термином «стохастика» понимается соединение элементов теории
вероятностей
приходится
и
математической
осуществлять
оценку
статистики.
шансов,
Учащимся
прогнозировать
постоянно
развитие
ситуаций, выдвигать гипотезы и предположения, рассуждать о возможностях
подтверждения той или иной гипотезы. Именно поэтому воспитанию
вероятностно- статистической культуры ребенка мы уделяем большое
внимание.
Важно помочь им правильно осознать реальную действительность, открыть
для себя вероятностную природу окружающего мира, показать, что в мире
случайностей можно не только хорошо ориентироваться, но и активно
действовать.
С
помощью
каких
же
средств
можно
организовать
формирование первоначальных стохастических представлений школьников?
К таковым можно отнести: стохастические игры; эксперименты
случайными
исходами;
статистические
исследования;
со
мысленные
статистические эксперименты и моделирование (имитацию) на знакомом для
детей материале.
Мы считаем, что основы стохастического мышления, элементарная
стохастическая интуиция не только нужны человеку в современном мире, но
и доступны на уровне начального образования, и поэтому изучение
элементов стохастики целесообразно и возможно в рамках школьного
обучения математике, и во внеклассной работе в начальной школе. На
начальном
этапе
важна
понятий, которые ребёнок
качественная
характеристика
вероятностных
должен усваивать постепенно – сначала
интуитивно, овладевая ими непосредственно в процессе проведения
экспериментов, играя.
Предлагаем вашему вниманию фрагменты внеклассных мероприятий
(математический кружок) проведённых нами на формирующем этапе.
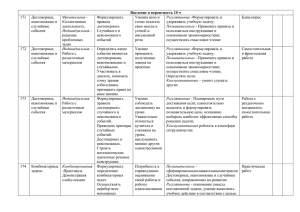
Темы математического кружка
№п
Тема
/п
Кол-во
часов
1.
Понятие случайного события
1
2.
Понятие невозможного события.
1
3.
Понятие достоверного события.
1
4.
Игра: « Звёздный час» по теме « Виды событий»
1
5.
« Математический К В Н»
1
Тема 1. Понятие случайного события.
Этап формирования понятия о случайных событиях.
Цель:
сформировать
понятие
случайного
события,
научить
распознавать случайные события.
Ход занятия
Математику многие любят за её вечные истины: дважды два всегда
четыре, сумма четных чисел четна и т.д.
Реальная жизнь не так проста и однозначна. Исходы многих явлений
заранее предсказать невозможно, какой бы полной информацией о них мы не
располагали. Нельзя например, сказать наверняка, какой стороной упадет
подброшенная вверх монета, когда в следующем году выпадет первый снег
или сколько человек в городе захотят в течение ближайшего часа позвонить
по телефону. Такие непредсказуемые явления называются случайными.
Оценивая
возможность наступления какого-либо
события, мы часто
говорим: «Это непременно произойдёт». Купив лотерейный билет, мы можем
выиграть, а можем и не выиграть,
завтра на уроке математики вас могут
вызвать к доске, а могут и не вызвать. Все это примеры случайных событий,
которые при одних и тех же условиях могут произойти, а могут и не
произойти. Мы будем обозначать события заглавными латинскими буквами и
записывать в фигурных скобках, например А={В следующем году
первый снег в Абакане выпадет в воскресенье}, В= {Свалившийся со стола
бутерброд упадет на пол маслом вниз}, С= {При бросании кубика выпадет
шестерка}, Д= {При бросании кубика выпадет четное число}.
А теперь задания вам: «Распознайте, какие из перечисленных событий
случайные?»
Вы купили в магазине телевизор, на который фирма- производитель
дает два года гарантии. Какие из следующих событий случайные:
А= {Телевизор не сломается в течение года};
В={Телевизор не сломается в течение двух лет};
С={В течение двух лет вам не придется платить за ремонт телевизора};
D= {Телевизор сломается на третий год}?
Ответ: А, В, D – случайные.
Тема 2. Понятие невозможного события
Цель: сформировать понятие невозможного события, научить
распознать невозможные события.
Содержание занятия.
Оценивая возможность наступления, какого либо события,
мы часто говорим: «Это мало вероятно», «это никогда не случится»
Есть и такие события, которые в данных условиях произойти не
смогут. Их называют невозможными событиями. Например:
Е = {В следующим году снег в Абакане вообще не выпадет};
F = {При бросание кубика выпадет семерка};
Задание учащимся: распознать, какие из перечисленных событий
невозможные:
1. Укажите, какие из перечисленных событий невозможные
А={футбольный матч «Спартак» - «Динамо» закончиться в ничью};
В={вы выиграете в беспроигрышной лотерее};
С={в полночь выпадет снег, а через 24 часа будет светить солнце};
D={Завтра будет контрольная по математике};
Е={30 февраля будет дождь}
F= {вас изберут президентом США};
G= {вас изберут президентом РОССИИ};
Ответ – G, E, F – невозможное
Тема 3.
Понятие достоверного события
Цель: сформировать понятие достоверного события, научить
распознать достоверные события.
Содержание занятия
Оценивая возможность наступления какого-либо события , мы
часто говорим: это непременно произойдет», «это очень возможно»
Если же события при данных условиях обязательно произойдет, то его
называют достоверным. Например: А = {в следующем году
в Абакане выпадет снег}, В = {при бросании кубика выпадет
число очков, меньшее 7}
Невозможные и достоверные события встречаются в жизни сравнительно
редко.
Поэтому можно сказать, что живем мы в жизни случайных
событий.
Задание распознать, достоверны ли события?
А = {Футбольный матч «Спартак» - «Динамо» закончится в ничью};
В = {Вы выиграете, участвуя в беспроигрышной лотерее};
С = {В полночь выпадет снег, а через 24 часа будет светить солнце};
О = {Завтра будет контрольная по математике};
Е = {30 февраля будет дождь};
F = {вас изберут президентом США};
G = {вас изберут президентом РОССИИ}?
Ответ: В.
Распознайте какие из перечисленных событий достоверны?
Вы купили в магазине телевизор, на который фирма производитель
дает два года гарантии. Какие из следующих событий невозможные
какие – случайные, какие – достоверные:
А = {Телевизор не сломается в течение года};
В = {Телевизор не сломается в течение двух лет};
С = {В течение двух лет вам не придется платить за ремонт телевизора};
В = {Телевизор сломается на третий год}?
Ответ: С – достоверное событие.
В коробке лежит 10 красных, 1 зеленая и 2 синих ручки. Из коробки наугад
вынимают два предмета. Какие из следующих
событий достоверные :
А = {Вынуты две красные ручки};
В = {Вынуты две зеленые ручки};
С = {Вынуты две синие ручки};
D = {Вынуты ручки двух разных цветов};
Е = {Вынуты две ручки};
F = {Вынуты два карандаша}?
Ответ: Е – достоверное.
Охарактеризуйте событие, в котором идет речь, как достоверное
Вы открыли эту книгу на любой странице и прочитали первое попавшееся
существительное. Оказалось, что:
а) в написании выбранного слова есть гласная буква;
б) в написании выбранного слова есть буква «о»;
в) в написании выбранного слова нет гласных букв;
г) в написании выбранного слова есть мягкий знак.
Ответ: а) – достоверное событие.
Подведение итогов.
Награждение.
Занятие 4
Игра: « Звездный час по теме Виды событий»
Вопросы отборочного тура:
1. От прямоугольной доски отрезали один угол. Сколько стало углов?
Ответ- 5 углов.
2. На языке древней Индии это число «сунья». Арабы перевели его на свой
язык, и стало оно называться «сифр» - цифра. Какое это число?
Ответ-0.
3. Какое самое любимое число в русских сказках и сказках многих других
народов?
Ответ-3.
4. Какое число древние люди считали символом устойчивости и прочности?
Ответ – 4.
5. У древних греков это число считалось счастливым и магическим. А в
далекие – далекие времена, когда люди с трудом учились считать, это число
означало «все». Какое это число?
Ответ – 3.
6. Какое число является символом женщины? Ответ – 2.
7. Какое число символизирует мужчину?
Ответ – 1.
8. Всем известно, что «Роллс-Ройс» - одна из самых дорогих автомашин.
Немногие из «новых русских» владеют ей. А у Владимира Ильича Ленина,
единственного из наших соотечественников, их было…
Сколько «Роллс-Ройсов» было у В. И. Ленина? [58]
Ответ – 2.
Первый тур
Варианты ответов:
Невозможные события – 1;
Случайные события – 2;
Достоверные события – 3.
Вопросы первого тура
Пример 1. Бросаем два кубика. Какие из следующих событий невозможные,
какие – случайные, а какие – достоверные:
В теории вероятностей принято все события называть случайными, а
невозможные
и
достоверные
рассматривать
разновидности.(практический метод)
А – {на кубиках выпало одинаковое число очков};
как
их
специальные
В – {сумма очков на кубиках не превосходит 12};
С – {сумма очков на кубиках равна 11};
D – {произведение очков на кубиках равно 11}?
Исход любого бросания можно описать двумя числами, выпавшими на
кубиках.
Например, (3, 1) означает, что на первом кубике выпало число 3, а на втором
– число 1.
При исходе (1, 1) событие А происходит, а при исходе (1, 2) – не происходит.
Значит, событие А случайное.
Событие В происходит при любом исходе: ведь каждое из двух чисел на
кубиках не превосходит 6, а значит, их сумма не превосходит 12.
Следовательно, событие В достоверное.
Событие С происходит при исходе (5, 6), но не происходит при исходе (2, 2).
Значит, оно случайное.
Наконец, для события D нет исхода, при котором оно происходит: число 11
нельзя представить в виде произведения двух целых чисел от 1 до 6. Значит,
это событие невозможное.
2. В коробке 3 красных, 3 желтых, 3 зеленых шара. Вытаскиваем наугад 4
шара. Какие из следующих событий невозможные, какие – случайные, а
какие – достоверные:
А – {все вынутые шары одного цвета};
В – {все вынутые шары разных цветов};
С – {среди вынутых шаров есть шары разных цветов};
D – {среди вынутых есть шары всех разных цветов}?
Событие А – невозможное: нельзя вытащить из коробки четыре шара одного
цвета, так как в ней только по три шара каждого цвета.
Событие В – тоже невозможное: шары в коробке трех цветов, а вынимаем мы
четыре шара.
Событие С – достоверное: ведь все четыре шара, как уже выяснили, не могут
быть одного цвета, поэтому среди них обязательно есть шары хотя бы двух
цветов.
1. Укажите, какие из следующих событий невозможные, какие –
достоверные, какие – случайные:
А – {Футбольный матч « Спартак» - «Динамо» закончится вничью};
В – {Вы выиграете, участвуя в беспроигрышной лотерее};
С – {В полночь выпадет снег, а через 24 часа будет светить солнце};
D – {Завтра будет контрольная по математике};
E – {30 февраля будет дождь};
F – {Вас изберут президентом США};
G – {Вас изберут президентом России}.
Ответ: случайные – А, D, F; достоверные – В; невозможное – Е, С, F.
2. Вы купили в магазине телевизор, на который фирма – производитель дает
два года гарантии. Какие из следующих событий невозможные, какие –
случайные, какие – достоверные:
А – {Телевизор не сломается в течение года};
В – {Телевизор не сломается в течение двух лет};
С – {В течении двух лет вам не придется платить за ремонт телевизора};
D – {Телевизор сломается на третий год}?
Ответ: случайные – D, С; достоверные – С; невозможное – А, В.
3. Три господина, придя в ресторан, сдали в гардероб свои шляпы.
Расходились по домам они уже в темноте и разобрали шляпы наугад. Какие
из следующих - невозможные, какие – достоверные, какие – случайные:
А – {Каждый надел свою шляпу};
В – {Все недели чужие шляпы};
С – {Двое недели чужие шляпы, а один - свою};
D – {Двое надели свои шляпы, а один - чужую}?
4. В игре «Любовь с первого взгляда» участвуют трое юношей, три девушки.
Каждый юноша выбирает одну из девушек, а каждая девушка - одного из
юношей. Если юноша и девушка выбирают друг друга, то образуется пара.
Какие из следующих событий невозможные, какие – достоверные, какие –
случайные:
А – {Не образовалось ни одной пары};
В – {Образовалась одна пара};
С – {Образовалось две пары};
D – {Образовалось три пары}?
Второй тур
Из 10 предложенных букв составить длинное слово:
Д, О, Т, С, В, Е, Р, Ы, А, Н.
(Достоверные)
Третий тур
6. Вини – Пух, Пятачок и все – все – все садятся за круглый стол праздновать
день рождения. При каком количестве всех – всех – всех событие А = {Вини –
Пух и Пятачок будут сидеть рядом} является достоверным, а при каком –
случайным?
7.В школе учится Мучеников. При каких значениях N событие А = {в школе
есть ученики с совпадающими днями рождения} является случайным, а при
каких – достоверным? Выясните, произошло ли это событие школе. А в
вашем классе?
8. Среди 100 билетов школьной благотворительной лотереи 20 выигрышных.
Сколько билетов вам надо купить, чтобы событие А = {вы ничего не
выиграете} было невозможным?
9. В шкафу 10 пар ботинок с 36 – го по 45 – й размер – по одной паре
каждого размера. Ботинки достают из шкафа наугад. Какие наименьшее
количество ботинок надо вынуть из шкафа, чтобы событие А = {из вынутых
ботинок можно составить хотя бы одну пару} было достоверным?
10. В классе учится 10 мальчиков и 20 девочек. Какие из следующих событий
являются для того класса невозможными, какие – случайными, какие –
достоверными:
А – {В классе есть два человека, родившихся в разные месяцы};
В – {В классе есть два человека, родившихся в одном месяце};
С – {В классе есть два мальчика, родившихся в одном месяце};
D – {В классе есть две девочки, родившиеся в одном месяце};
E – {Все мальчики родились в разные месяцы};
F – {Все девочки родились в разные месяцы};
O – {Есть мальчик и девочка, родившиеся в одном месяце};
H – {Есть мальчик и девочка, родившиеся в разные месяцы}?
Автобусу, в котором едет 15 пассажиров, предстоит сделать 10 остановок.
Какие из следующих событий невозможные, какие – случайные, какие –
достоверные:
А – {Все пассажиры выйдут и автобуса на разных остановках};
В – {Все пассажиры выйдут на одной остановке};
С – {На каждой остановке хоть кто – то выйдет};
D – {Найдется остановка, на которой никто не выйдет};
E – {На всех остановках выйдет четное число пассажиров};
Р – {На всех остановках выйдет не четное число пассажиров}?
На координатной прямой в начале отсчета стоит фишка. После каждого
бросания монеты она сдвигается на единицу вправо, если выпал «орел», или
на единицу влево, если выпала «решка». Какие из следующих событий
невозможные, какие – случайные, какие – достоверные:
А – {После 4-х бросаний фишка находится в точке с координатой 0};
В – {После 3-х бросаний фишка находится в точке с координатой 2};
С – {После 5-ти бросаний фишка находится в точке с координатой 5};
D – {После 50-ти бросаний фишка находится в точке с координатой 25};
E – {После 50-ти бросаний фишка находится в точке с координатой 26}?
На тетрадный лист в линейку бросают зубочистку. Расстояние между
линейками 1см. При какой длине зубочистки событие А = {Зубочистка
пересекла 10 линий} будет невозможным, при какой – случайным, при какой
– достоверным?
Игра со зрителями
Составить 2 достоверных, 2 случайных, 2 невозможных события
Победитель получает звезду, которую отдает любимому из участников
Финал
Остается 2 участника, их задача как можно больше составить слов из слова
СОБЫТИЕ например: быт, соты, бытие…
НАГРАЖДЕНИЕ ПОБЕДИТЕЛЯ
Занятие 5
Тема : «Математический КВН»
Цель занятия: обобщить ранее на конкретных примерах.
1. Конкурс «Разминка»;
2. Конкурс капитанов;
3. Конкурс «Ты мне, я тебе»;
4. Конкурс лидеров;
5. Конкурс «Определите вид события»;
6. Подведение итогов;
7. Награждение команд.
Таким
образом, основы стохастического мышления, элементарная
стохастическая интуиция доступны на уровне начального образования. Как
утверждает А.Плоцки, «из-за своей
специфики стохастика может быть
математикой, понимаемой каждым учеником как математика, открытая им
самим».