Название урока: Взаимно обратные функции

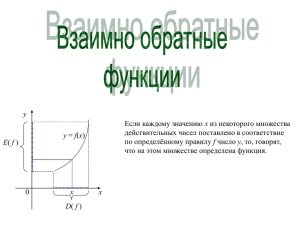
Урок подготовила учитель математики и информатики
высшей квалификационной категории
МОУ Платошинская средняя
общеобразовательная школа
Сапожникова Елена Семеновна
Урок в 10 классе по теме «Взаимно-обратные функции»
(по программе Алимова Ш.А.)
Тип урока: комбинированный.
Цели урока:
Образовательные:

Повторить и обобщить знания обучающихся по теме «Функция», изученные в 9 классе.

Познакомиться со взаимно обратными функциями, изучить условия существования
обратной функции и ее свойства, научиться строить графики обратных функций.
Развивающие:

Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные
качества: способность к «видению» проблемы.

Формировать умения чётко и ясно излагать свои мысли, исследовать, анализировать,
сравнивать, делать выводы.

Развивать интерес учащихся к самостоятельному творчеству.

Развивать пространственное воображение учащихся.
Воспитательные:

Воспитывать умение работать с имеющейся информацией в необычной ситуации.

Воспитывать аккуратность и добросовестность.

Осуществлять эстетическое воспитание.
Оборудование:

экран;

ноутбук;

мультимедийный проектор;

приложение к уроку: (Презентация.) – на электронном носителе;
Средства обучения: компьютеры, программа Excel, медиапроектор, слайдовая презентация.
Демонстрации: графики функций, построенные в одной системе координат.
Формы организации учебной деятельности: индивидуальная, диалог, работа с текстом слайда,
исследовательская работа в в тетради.
Методы: наглядный, словесный, графический, исследовательский.
Этапы урока:
1. Постановка цели урока и мотивация учебной деятельности. 2 мин
2. Повторение пройденного материала по теме «Функции и их графики». 10 мин
3. Этап объяснения нового материала. 10 мин
4. Операционно-исполнительная часть. Этап закрепления. 10 мин
5. Контроль знаний (рабочий лист с тестом на бумажном носителе) 5 мин
6. Задание на дом. 1 мин
7. Рефлексивно-оценочный этап. 2 мин
Ход урока.
1. Вступительное слово учителя. Установочная беседа. Психологический настрой учащихся.
Сегодняшний урок у вас не совсем обычный: учитель математики Елена Семеновна из
Платошинской средней школы, гости – учителя математики и методисты вашей школы и
управления образования Пермского района.
На уроке мы с вами должны повторить и обобщить знания обучающихся по теме
«Функция», изученные в 9 классе, познакомиться со взаимно обратными функциями, изучить
условия существования обратной функции и ее свойства, научиться строить графики обратных
функций. Пожелаем друг другу успехов и плодотворной работы.
2. Повторение пройденного материала по теме «Функции и их графики». Презентация.
Слайды 2-10.
Фронтальная работа с классом.
Какой из графиков соответствует графику функции
у=х3?
1.
2.
3.
4.
Какой из графиков соответствует графику функции
у=х?
1.
2.
3.
4.
Какой из графиков соответствует графику
функции
у= IхI?
1.
3.
2.
4.
Какой из графиков соответствует графику функции
у= х?
1.
у
у
3.
х
2.
х
у
у
х
4.
х
Какой график соответствует функции?
у
а
у
б
2
1
-1
2
1
х
0 1
-1
-2 -1
-2
0
-2
у
г
х
1
у
в
2
1
2
-1
1
-2
-1
-2
0
х
0 1
х
1
-2
-1
Какой функции
соответствует график?1
1
1. у = х3 у 2.х3
а
у
б
3. у = х4 4. у = х-2 у 5.х2
у
г у
6. у = хв-1
у
х
д
х
х
е
у
х
у
х
х
1 2 3 4 5 6
г е а д б в
3. Изучение нового материала. Обучающая беседа с элементами исследования и
демонстрацией (слайды 11-24)
Если каждому значению х из некоторого
множества
действительных
чисел
поставлено
в
соответствие
по
определённому правилу f число у, то,
говорят, что на этом множестве определена
функция.
y
y = f(x)
E( f )
0
х
x
D( f )
Укажите область определения данной
на графике функции
D(y)=[-4;2]
4.
Укажите область определения данной
на графике функции
D(y)=(-:0)U(0;+)
Укажите область значений данной
на графике функции
y
2
0
x
Прямая
Задача.
Обратная
у = f (x), x – дано.
Найти значение у при заданном
значении х.
Задача.
у = f (x), у - дано.
Найти значение х при заданном
значении у.
Дано: у = 2х + 3
Дано: у = 2х + 3, у (х) = 42
Найти: у (5)
Найти: х
Решение:
Решение:
у (5) = 2 · 5 + 3 = 13
42 = 2х + 3
Ответ: у (5) = 13
2х = 39
х = 19,5
Ответ: у (19,5) = 42
Пример зависимости. Каждому значению функции соответствует одно значение аргумента.
Для таких функций можно выразить обратную зависимость значений аргумента от
значений функции.
Дано:
v(t )  v0  gt
Найти:
t–?
Обратимая функция
Решение:
v0  gt  v
gt  v0  v
v v
t 0
g
, т.е.
t (v ) 
v0  v
g
Обратная функция к v(
t)
Если функция у = f ( х ) принимает каждое своё
значение у только при одном значении х, то эту
функцию называют обратимой.
Обратимые функции
Необратимая функция
у  2х  2
1
у  2
х
у  х2
ух
х1  у
3
х2   у
Пусть у = f(x) – обратимая функция. Тогда каждому у из
множества
значений
функции
соответствует
одно
определённое число х из области её определения, такое, что
f(x) = y. Это соответствие определяет функцию х от у,
которую обозначим х = g(y). Поменяем местами х и у: у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x).
Задание.
Дано:
у
1
х2
(1)
Найти функцию, обратную данной
у = g(x)
Решение:
1
у
х2
1
х2
у
1
х  2
у
Ответ:
у  2
у  2
1
x
1
х
(2)
Функция (2) обратна к функции (1). Эти функции называют
взаимно-обратными.
Найдите область определения и область значений взаимно-обратных функций.
у
у
у  2
1
у
х2
1
х
2
0
2
х
0
1. D(у)=(-∞;2)∪(2;+∞)
1. D(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
1. Область определения обратной функции g(x)
совпадает с множеством значений исходной f, а
множество значений обратной функции g(x)
совпадает с областью определения исходной
функции f(x):
D(g(x) ) = E(f(x)), E(g(x)) = D(f(x)).
2. Монотонная функция является обратимой:
если функция f возрастает, то обратная к ней
функция g(x) также возрастает;
если функция f убывает, то обратная к ней
функция g(x) также убывает.
х
3. Если функция имеет обратную, то график
обратной функции симметричен графику данной
функции относительно прямой у = х.
у
у=х
(х0;у0)
у0
(у0;х0)
х0
0
х
у
у=f(x)
y=x2,х<0
у=g(x)
3
-2
0
у
3
0
х
х
-2
у х
1. D(f)=R
1. D(g)=R
1. D(y)=(-∞;0]
1. D(y)=[0;+∞)
2. E(f)=R
2. E(g)=R
2. E(y)=[0;+∞)
2. E(y)=(-∞;0]
3. возрастающая 3. возрастающая
4. Закрепление знаний.
3. убывающая 3. убывающая
Построить график функции, обратной данной.
у
у
1
1
х
1
0
0
1
х
у  х3
у
Дано: у = х3
у3 х
Построить функцию,
обратную к данной.
х3  у
Решение:
0
х3 у  у3 х
Построить график функции, обратной данной.
у
у
1
1
0
1
х
0
1
х
у  х3
Дано: у = х3
у
у3 х
Построить график
функции, обратной к
данной.
Решение:
х3  у
х3 у  у3 х
5. Контроль знаний.
0
х
х
6. Задание на дом: изучить стр. 46-50, решить № 132, № 133, № 134
7. Рефлексивно-оценочный этап.
•
На уроке я научился(лась)………………………….
•
На уроке мне интересно было …………………....
•
Трудно было ………………………………………….
•
Знания,
полученные
на
…………………………………………
уроке,
я
могу
использовать