Задание 4 (построение сетки)

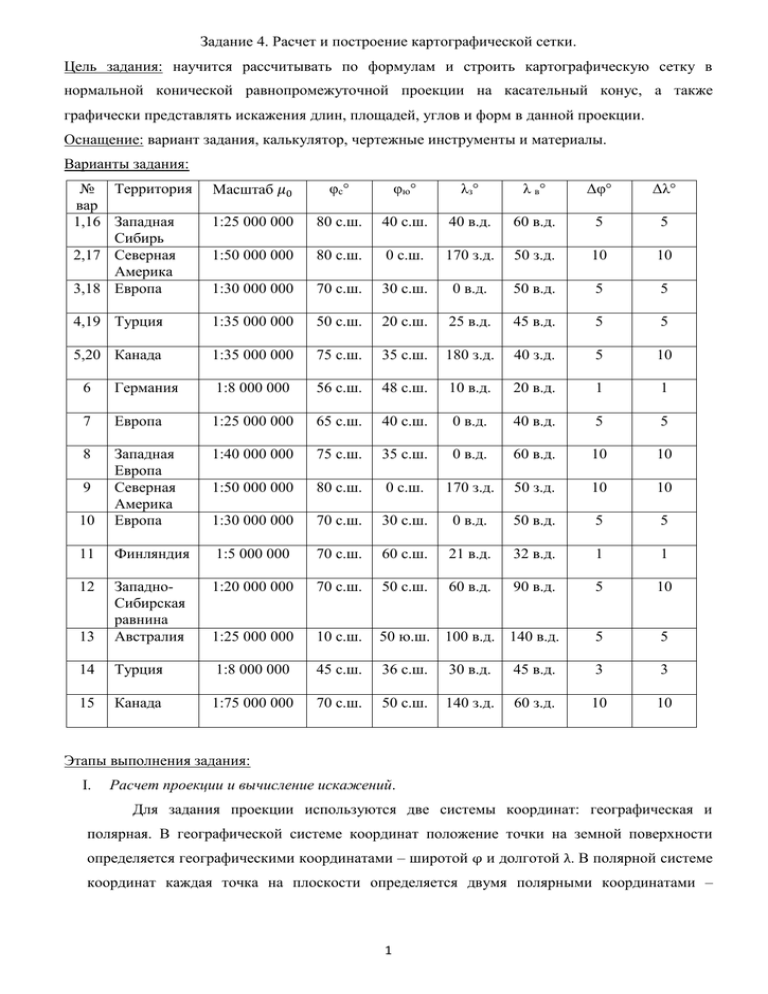
Задание 4. Расчет и построение картографической сетки.
Цель задания: научится рассчитывать по формулам и строить картографическую сетку в
нормальной конической равнопромежуточной проекции на касательный конус, а также
графически представлять искажения длин, площадей, углов и форм в данной проекции.
Оснащение: вариант задания, калькулятор, чертежные инструменты и материалы.
Варианты задания:
№ Территория
вар
1,16 Западная
Сибирь
2,17 Северная
Америка
3,18 Европа
Масштаб 𝜇0
φс°
φ ю°
λз°
λ в°
Δφ°
Δλ°
1:25 000 000
80 с.ш.
40 с.ш.
40 в.д.
60 в.д.
5
5
1:50 000 000
80 с.ш.
0 с.ш.
170 з.д.
50 з.д.
10
10
1:30 000 000
70 с.ш.
30 с.ш.
0 в.д.
50 в.д.
5
5
4,19 Турция
1:35 000 000
50 с.ш.
20 с.ш.
25 в.д.
45 в.д.
5
5
5,20 Канада
1:35 000 000
75 с.ш.
35 с.ш.
180 з.д.
40 з.д.
5
10
6
Германия
1:8 000 000
56 с.ш.
48 с.ш.
10 в.д.
20 в.д.
1
1
7
Европа
1:25 000 000
65 с.ш.
40 с.ш.
0 в.д.
40 в.д.
5
5
8
1:40 000 000
75 с.ш.
35 с.ш.
0 в.д.
60 в.д.
10
10
1:50 000 000
80 с.ш.
0 с.ш.
170 з.д.
50 з.д.
10
10
10
Западная
Европа
Северная
Америка
Европа
1:30 000 000
70 с.ш.
30 с.ш.
0 в.д.
50 в.д.
5
5
11
Финляндия
1:5 000 000
70 с.ш.
60 с.ш.
21 в.д.
32 в.д.
1
1
12
1:20 000 000
70 с.ш.
50 с.ш.
60 в.д.
90 в.д.
5
10
13
ЗападноСибирская
равнина
Австралия
1:25 000 000
10 с.ш.
50 ю.ш. 100 в.д. 140 в.д.
5
5
14
Турция
1:8 000 000
45 с.ш.
36 с.ш.
30 в.д.
45 в.д.
3
3
15
Канада
1:75 000 000
70 с.ш.
50 с.ш.
140 з.д.
60 з.д.
10
10
9
Этапы выполнения задания:
I.
Расчет проекции и вычисление искажений.
Для задания проекции используются две системы координат: географическая и
полярная. В географической системе координат положение точки на земной поверхности
определяется географическими координатами – широтой φ и долготой λ. В полярной системе
координат каждая точка на плоскости определяется двумя полярными координатами –
1
полярным углом δ (угол между начальным направлением и направлением на заданную точку)
и полярным радиусом 𝜌 (расстояние от полюса до заданной точки).
Если спроецировать земной шар на касательный конус и развернуть на плоскость,
получим:
Где S0 – центр (полюс) проекции, φ0 – широта параллели касания, λ 0 – долгота осевого
меридиана, δ – угол между соседними меридианами, 𝜌0 – радиус параллели касания, ∆𝜌 –
расстояние между двумя соседними параллелями (const, т.к. проекция равнопромежуточная), к –
хорда, стягивающая два соседних меридиана напрямую.
Для построения проекции необходимо вычислить полярные координаты 𝜌 и δ:
𝜌 = 𝑓 (𝜑)
(Уравнение конической проекции
𝛿 = 𝛼 (𝜆)
в общем виде)
𝛼 – коэффициент пропорциональности долгот на карте
Для вычисления величин, необходимых для построения, следовать следующему алгоритму.
1. Найти широту параллели касания φ0 и долготу осевого меридиана λ 0 по формулам:
𝜑с + 𝜑ю
2
λв+λз
𝛌𝟎 =
2
𝝋𝟎 =
2. Найти коэффициент пропорциональности долгот α и угол между смежными меридианами
на карте δ:
𝜶 = sin 𝜑0
𝜹 = 𝛼 ∙ ∆λ°
где ∆λ – шаг сетки по долготе в градусах.
3. Найти радиус параллели касания 𝜌0 :
𝝆𝟎 = 100 ∙ 𝜇0 ∙ 𝑅 ∙ ctg 𝜑0 см
2
где R=6371116 м (радиус Земли), 100 – коэффициент для перевода радиуса Земли в см, 𝜇0 –
главный масштаб.
4. Рассчитать расстояние между двумя соседними параллелями ∆𝜌 (∆𝜌 = 𝑐𝑜𝑛𝑠𝑡, т. к. проекция
равнопромежуточная):
∆𝝆 = 100 ∙ 𝜇0 ∙ 𝑅 ∙ ∆𝜑 ∙
1
см
𝜌0
где R=6371116 м – радиус Земли, 100 – коэффициент для перевода радиуса Земли в см, 𝜇0 –
главный масштаб, ∆𝜑 – шаг сетки по широте в градусах, 𝜌0 = 57,29578 – градусная мера
радиана.
5. Найти радиусы всех остальных параллелей сетки:
𝝆 = 𝜌0 − (+)𝑁 ∙ ∆𝜌 см
где N – порядковый номер параллели от параллели касания к северу (−) или югу (+) от
параллели касания (1, 2, 3 и т.д.).
6. Рассчитать стягивающие хорды на двух любых параллелях для построения меридиан:
𝑲 = 2 ∙ 𝜌 ∙ sin
𝛿
см
2
7. Вычислить параметры эллипса искажения.
Карте присущи искажения длин, площадей, углов и форм.
Искажения длин выражаются в том, что масштаб длин на карте изменяется при
переходе от одной точки к другой, а также по разным направлениям из данной точки.
Искажения площадей выражаются в том, что в разных местах карты масштаб площадей
различен, поэтому нарушаются соотношения площадей различных географических объектов.
Искажения углов заключаются в том, что углы между направлениями на карте не равны
соответствующим углам на поверхности эллипсоида и, следовательно, не равны
соответствующим углам на местности. Искажения форм заключаются в том, что фигуры
объектов на карте не подобны фигурам соответствующих географических объектов на
местности.
Все виды искажений связаны друг с другом и изменение любого из них влечет за
собой изменение других.
Показателем искажений длин в данной точке по данному направлению является
частный масштаб длин 𝜇, выраженный в долях главного масштаба 𝜇0 . Частный масштаб 𝜇
изменяется в данной точке в зависимости от направления. По одному из направлений 𝜇
имеет наибольшее значение, обозначим его a, по другому – наименьшее значение, обозначим
его b. Эти два направления взаимно перпендикулярны, и их называют главными
направлениями. Поскольку в каждой точке карты можно провести меридиан и параллель,
особо выделяют частные масштабы длин по меридианам m и по параллелям n.
3
Наиболее полно все виды искажений в данной точке карты можно представить в виде
эллипса искажений. Эллипс искажений в данной точке карты изображает бесконечно малый
крут на поверхности эллипсоида. Его полуоси а и b, они ориентированы по главным
направлениям. Форма эллипса характеризует искажения углов и форм: они искажены тем
больше, чем больше эллипс отличается от окружности. Площадь эллипса пропорциональна
искажению площадей, и она тем больше, чем больше искажены площади.
Для построения эллипса искажения на карте необходимо выбрать его условный
масштаб. Для этого радиус 𝑟0 бесконечно малого кружка, взятого на поверхности
эллипсоида, при изображении его на карте в масштабе 𝜇0 принимают равным какому-либо
конечному значению, например, 𝑟0 𝜇0 = 0,5 см. Тогда все величины, используемые для
построения эллипса искажения, также примут конечные значения.
Размер и характер искажений, которые каждый эллипс демонстрирует, следует
относить к точке карты, в которой находится центр эллипса.
Рассчитать параметры эллипса искажения на северной и южной параллелях:
r=m=0,5 см; 𝒏𝝋𝟎 = 0,5 см
II.
𝒏𝒄 =
sin 𝜑0 ∙ 𝜌𝑐
∙ 0,5 см
100 ∙ 𝜇0 ∙ 𝑅 ∙ cos 𝜑𝑐
𝒏ю =
sin 𝜑0 ∙ 𝜌ю
∙ 0,5 см
100 ∙ 𝜇0 ∙ 𝑅 ∙ cos 𝜑ю
Построение картографической сетки и эллипса искажений.
В центре листа формата А4 поставить точку и через нее провести вертикальную линию –
осевой меридиан. Найти полюс проекции, отложив о центральной точки вверх по осевому
меридиану значение радиуса параллели касания. С помощью циркуля провести параллель
касания из полюса проекции. Аналогично провести все остальные параллели, используя
значения радиусов соответствующих параллелей или значение расстояния между двумя
соседними параллелями ∆𝜌. Меридианы построить, используя значение угла между двумя
соседними меридианами δ или значения хорд, стягивающих два соседних меридиана на двух
параллелях.
Построить эллипсы искажения на трех параллелях (северной, южной и параллели
касания) в точке их пересечения с осевым меридианом, используя рассчитанные значения
полуосей m и n.
Построить внутреннюю рамку таким образом, чтобы попали все крайние параллели и
меридианы. На расстоянии 10 мм от внутренней рамки построить внешнюю рамку более толстой
линией. Между внутренней и внешней рамками подписать значения параллелей вдоль западной
и восточной, меридианов – вдоль северной и южной рамок.
4
Все построения выполнить карандашом, затем обвести черной гелевой ручкой, лишние
карандашные линии стереть. Над северной рамкой подписать название территории, под южной
рамкой – масштаб.
Допускается построение сетки в электронном режиме.
Оформление работы: работа должна быть оформлена в соответствии с образцом (см. стр. 6).
Сроки выполнения работы: задание рассчитано на одно практическое занятие.
5
Пример выполненного задания:
Задание 4. Вычисление и построение картографической сетки
в равнопромежуточной конической проекции.
Вариант 1.
Дано: Канада
λ °з = 180° з. д.
λ °в = 40° з. д.
∆𝜑 = 5
∆λ ° = 10
𝜇0 = 1: 50 000 000
𝜑с° = 75° с. ш.
𝜑ю° = 35° с. ш.
°
Расчеты:
1. 𝝋𝟎 =
𝜑с +𝜑ю
2
=
75° +35°
2
= 55° с. ш. ;
𝛌𝟎 =
λ в +λ з
2
=
40° +180°
2
= 110° з. д.
2. 𝜶 = sin 𝜑0 = sin 55° = 0,8192; 𝜹 = 𝛼 ∙ ∆λ = 0,8192 ∙ 10 = 8,192° = 8° 11` 30"
3. 𝝆𝟎 = 100 ∙ 𝜇0 ∙ 𝑅 ∙ ctg 𝜑0 = 100 ∙
1
1
∙
50 000 000
6 371 116 ∙ ctg 55° = 8,92 см
1
4. ∆𝝆 = 100 ∙ 𝜇0 ∙ 𝑅 ∙ ∆𝜑 ∙ 𝜌0 = 100 ∙ 50 000 000 ∙ 6 371 116 ∙ 5 ∙ 0,0175 = 1,11 см
5. 𝝆𝒄 = 𝜌0 − 4 ∙ ∆𝜌 = 8,92 − 4 ∙ 1,11 = 4,48 см;
𝛿
6. 𝑲с = 2 ∙ 𝜌с ∙ sin 2 = 2 ∙ 4,48 ∙ sin
8° 11′ 30"
2
𝝆ю = 𝜌0 + 4 ∙ ∆𝜌 = 13,36 см
𝛿
= 0,64 см; 𝑲ю = 2 ∙ 𝜌ю ∙ sin 2 = 2 ∙ 13,36 ∙ sin
8° 11′ 30"
2
= 1,91 см
7. r=m=0,5 см; 𝒏(𝝋𝟎 ) = 0,5 см
𝒏𝒄 =
sin 𝜑0 ∙ 𝜌𝑐
∙ 0,5 =
100 ∙ 𝜇0 ∙ 𝑅 ∙ cos 𝜑𝑐
100 ∙
𝒏ю =
sin 𝜑0 ∙ 𝜌ю
∙ 0,5 =
100 ∙ 𝜇0 ∙ 𝑅 ∙ cos 𝜑ю
100 ∙
sin 55° ∙ 4,48
1
∙ 6 371 116 ∙ cos 75°
50 000 000
∙ 0,5 = 0,56 см
sin 55° ∙ 13,36
∙ 0,5 = 0,52 см
1
∙ 6 371 116 ∙ cos 35°
50 000 000
6
Студ. II к.: Иванов И. И.
Кафедра: Экономической и
социальной географии
Балл:
Дата:
Преподаватель:
7