xtxtxtxt 2 π 2 2 π 2 2 π 3 2 π 1 4 3 2 x
реклама
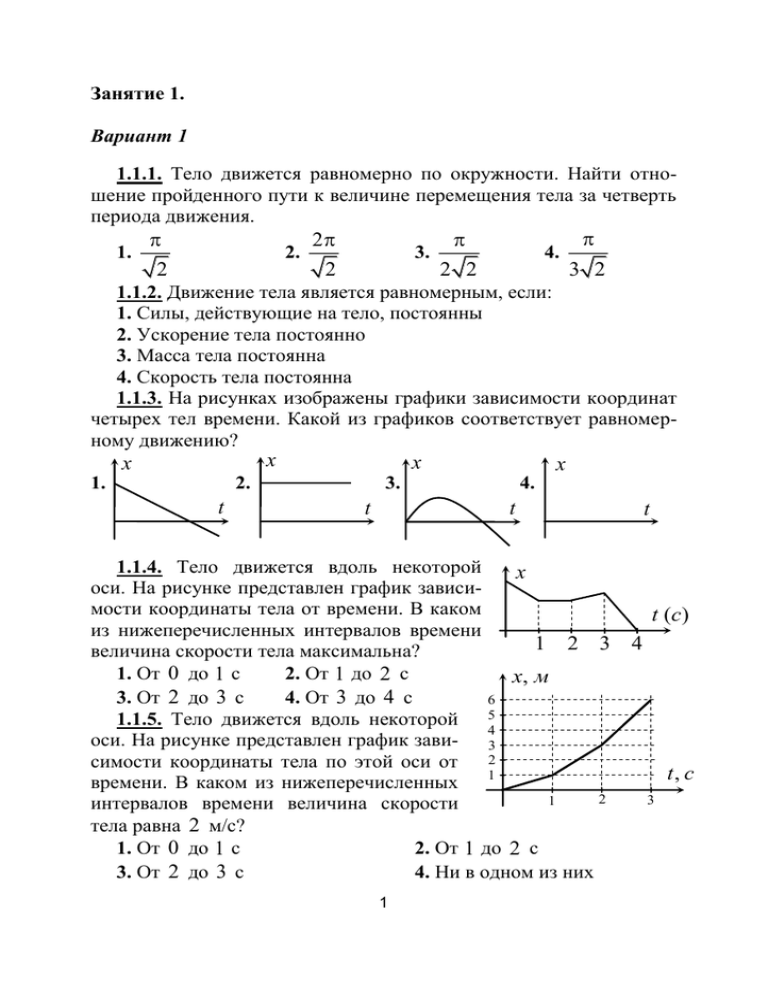
Занятие 1. Вариант 1 1.1.1. Тело движется равномерно по окружности. Найти отношение пройденного пути к величине перемещения тела за четверть периода движения. 1. 2 2. 2 2 3. 4. 2 2 3 2 1.1.2. Движение тела является равномерным, если: 1. Силы, действующие на тело, постоянны 2. Ускорение тела постоянно 3. Масса тела постоянна 4. Скорость тела постоянна 1.1.3. На рисунках изображены графики зависимости координат четырех тел времени. Какой из графиков соответствует равномерному движению? x x 1. x 2. t x 3. 4. t t 1.1.4. Тело движется вдоль некоторой x оси. На рисунке представлен график зависимости координаты тела от времени. В каком из нижеперечисленных интервалов времени 1 2 3 величина скорости тела максимальна? 1. От 0 до 1 с 2. От 1 до 2 с x, м 3. От 2 до 3 с 4. От 3 до 4 с 6 1.1.5. Тело движется вдоль некоторой 5 4 оси. На рисунке представлен график зави- 3 2 симости координаты тела по этой оси от 1 времени. В каком из нижеперечисленных 2 1 интервалов времени величина скорости тела равна 2 м/с? 1. От 0 до 1 с 2. От 1 до 2 с 3. От 2 до 3 с 4. Ни в одном из них 1 t t (c ) 4 t, с 3 1.1.6. Автомобиль, двигаясь с постоянной скоростью, проходит расстояние 100 м за 5 с. Чему равна скорость автомобиля? 1. 48 км/ч 2. 64 км/ч 3. 72 км/ч 4. 84 км/ч 1.1.7. По периметру прямоугольника со сторонами 3 и 4 см маленький жук проходит за время 7 с. Какое время затратит жук, чтобы пройти с той же скоростью вдоль диагонали этого прямоугольника? 1. 5 с 2. 2,5 с 3. 2 с 4. 1 с 1.1.8. Одну треть пути от города А до города В автомобиль проехал с постоянной скоростью, затратив на это движение время t . Затем автомобиль увеличил скорость втрое и остаток пути проехал с этой новой скоростью. Какое время автомобиль затратил на весь путь? 1. 5t / 3 2. 2t 3. 7t / 3 4. 8t / 3 1.1.9. Тело движется вдоль некотоvx , м / c рой оси. На рисунке представлен гра3 фик зависимости проекции скорости 2 тела на эту ось от времени. Какой 1 t, с путь пройдет тело за интервал време2 3 1 -1 ни от t 0 до t 3 с? -2 -3 1. 3/ 2 м 2. 5 / 2 м 3. 7 / 2 м 4. 9 / 2 м 1.1.10. Поезд едет со скоростью v1 . В поезде по направлению его движения идет человек со скоростью v2 . Чему равна скорость человека относительно земли? 1. v1 v2 2. v1 v2 3. v12 v22 4. v12 v22 Вариант 2 1.2.1. Два автомобиля движутся по прямому шоссе, направленному с севера на юг. Первый автомобиль движется на юг со скоростью v , второй – на север со скоростью 2v . Чему равна скорость второго автомобиля относительно первого? 1. v , направлена на юг 2. v , направлена на север 3. 3v , направлена на юг 4. 3v , направлена на север 2 1.2.2. Скорость лодки в стоячей воде 10 км/ч, скорость течения – 5 км/ч. Во сколько раз время движения между двумя городами, расположенными на берегу реки, вниз по течению меньше времени движения между этими городами вверх по течению? 1. В 2 раза 2. В 3 раза 3. В 4 раза 4. В 5 раз 1.2.3. Два тела одновременно начинают равномерно двигаться из одной точки по одной и той же окружности радиусом R . Скорости тел направлены противоположно и одна из них в три раза больше другой. На каком расстоянии от начальной точки произойдет первая встреча тел? 1. R / 3 2. 3R / 2 3. 3R 4. 2R 1.2.4. Два тела находятся на расстоянии l друг от друга. Тела одновременно начинают двигаться навстречу друг другу с постоянными скоростями v1 и v2 . Через какое время произойдет встреча тел? 1. l v1 v2 2. l v1 v2 3. v1 v2 l 4. v1 v2 l 1.2.5. Первый пешеход проходит расстояние между пунктами А и В за время 4 ч, второй – за время 2 ч. Через какое время после выхода встретятся пешеходы, если выйдут одновременно навстречу друг другу из пунктов А и В? 1. 4 / 3 ч 2. 5 / 3 ч 3. 2 ч 4. 7 / 3 ч 1.2.6. Вагон длиной l движется равномерно со v1 скоростью v1 . Провожаv2 ющий бежит со скоростью v2 ( v1 v2 ). На какое расстояние переместится провожающий, пробежав вдоль всего вагона (начальное положение вагона и провожающего показано на рисунке)? 1. lv2 v1 v2 2. lv1 v1 v2 3. lv1 v1 v2 4. lv2 v1 v2 1.2.7. Автомобиль движется между городами А и В. Первую половину пути автомобиль прошел с постоянной скоростью 40 км/ч, 3 вторую – с постоянной скоростью 60 км/ч. Чему равна средняя скорость автомобиля на всем пути? 1. 50 км/ч 2. 51 км/ч 3. 48 км/ч 4. 52 км/ч 1.2.8. Поезд едет со скоростью v1 . В поезде перпендикулярно направлению его движения идет человек со скоростью v2 . Чему равна скорость человека относительно земли? 1. v1 v2 2. v1 v2 3. v12 v22 4. v12 v22 1.2.9. Лодка пересекает реку. Под каким углом к берегу расположена траектория, на переправу по которой затрачи вается минимальное время (см. рисунок)? Скорость лодки относительно воды и скорость течения равны соответственно v и u . 1. arctg (v / u) 2. arcctg (v / u) u 3. 90 4. 45 1.2.10. Два катера, идущие вниз по реке с разными скоростями, одновременно обогнали плывущий по течению плот. Затем через одно и то же время катера повернули назад и поплыли с прежними относительно воды скоростями. Какой из катеров – быстрый или медленный – раньше встретит плот? 1. Быстрый 2. Медленный 3. Одновременно 4. Мало информации для ответа 4 Занятие 1. Вариант 1 Номер задачи 1.1.1-1.1.10 1 2 3 4 5 6 7 8 9 10 Ответ 3 4 1 4 2 3 2 1 4 2 Номер задачи 1.2.1-1.2.10 1 2 3 4 5 6 7 8 9 10 Ответ 4 2 4 2 1 1 3 3 1 3 Вариант 2 5 Глава 1. Путь, перемещение, скорость. Движение с постоянной скоростью. Относительность движения В рамках этой темы необходимо знать ряд простых определений, понимать логику определения скорости и закона сложения скоростей. Перемещением тела называется вектор, связываS ющий начальное и конечное положение тела, а r R пройденным путем – длина траектории. Поэтому величина (или модуль) перемещения – это расстояR ние от конечной до начальной точки по прямой, а путь – расстояние траектории тела. В задаче 1.1.1 пройденный телом за четверть периода путь – длина четверти окружности S 2πR / 4 , перемещение – r 2 R (см. рисунок), правильный ответ – 3. Скорость тела определяется как отношение перемещения тела r ко времени t , затраченному на это перемещение v r . t (1.1) Для прямолинейного движения в одном направлении для величины вектора скорости получаем из (1.1) v S , t (1.2) где S – путь, пройденный за время t . Если определение (1.1) приводит к одной и той же величине для любого интервала времени t , то скорость тела есть величина постоянная, а такое движение называется равномерным (задача 1.1.2 – ответ 4). В этом случае согласно (1.1) и (1.2) перемещение и пройденный путь линейно зависят от времени r vt и S vt . По этой причине линейно зависят от времени и координаты тела в любой системе координат. Поэтому графиком зависимости координат тела от времени для равномерного движения является прямая (задача 1.1.3 – ответ 1). Как следует из (1.1), (1.2), наклон этой прямой определяется скоростью: чем больше скорость, тем «круче» наклонен график зависимости координаты тела от времени к оси времени. Поэтому в задаче 1.1.4 на каждом из интервалов времени - от 0 до 1 с, от 1 до 2 с, от 2 до 6 3 с и от 3 до 4 с движение тела будет равномерным, а самой большой скорость тела будет в интервале времени от 3 до 4 с, в котором наклон графика максимален (ответ 4). В задаче 1.1.5 нужно по графику зависимости координаты тела от времени найти его скорость. Это можно сделать так. Перемещение тела внутри каждого из интервалов времени – 0 - 1 , 1 - 2 и 2 - 3 с – разность координат тела вначале и в конце этого интервала. Поэтому из графика находим 1(м) 0(м) 1 м/с ; 1(c) 3(м) 1(м) v(1 2 c) 2 м/с ; 1(c) 6(м) 3(м) v(2 3 c) 3 м/с . 1(c) Таким образом, скорость тела равна 2 м/с внутри интервала времени 1 - 2 с (ответ 2). v(0 1 c) Задача 1.1.6 посвящена размерности скорости. Из определения заключаем, что размерность скорости есть расстояние . время И, следовательно, размерностью скорости могут быть километр час метр секунда сажень сутки (или любые другие отношения единиц расстояний и времени). Для пересчета скорости из одних единиц в другие нужно выразить расстояние и время в требуемых единицах. Например, в задаче 1.1.6 имеем v 100 м 100 103 км 100 км км 3, 6 72 1 5с 5 ч ч 5 ч 3600 (правильный ответ – 3). При движении с постоянной скоростью определения (1.1) или (1.2) могут быть применены к любым этапам движения. Например, в задаче 1.1.7 можно из данных о движении жука вдоль периметра 7 прямоугольника найти его скорость ( v 14 / 7 2 см/с), а затем использовать ее для описания движения жука вдоль диагонали (длина которой составляет 5 см): t1 5 / 2 2,5 с (правильный ответ 2). Аналогичные соотношения используются в задаче 1.1.8. Рассматривая движение автомобиля на одной трети пути, получаем t S / 3v , где S – расстояние между городами. А на оставшихся двух третях (с учетом трехкратного увеличения скорости) t1 2S / 9v 2t / 3 . Поэтому полное время движения равно t t1 5t / 3 (ответ 1). В задаче 1.1.9 следует использовать следующее свойство графика зависимости проекции скорости тела на некоторую ось от времени: площадь под этим графиком есть проекция перемещения тела на рассматриваемую ось. Причем площадь под участками графика, лежащими выше оси времени, нужно считать положительной, ниже оси времени – отрицательной. Если же все площадь под всеми участками графика считать положительной, площадь под графиком скорости дает пройденный телом путь. Находя площадь под данным в условии графиком, получаем S 3 3 3 9 м 2 2 2 2 (ответ – 4). Важным физическим законом, знание которого часто проверяется на едином государственном экзамене по физике, является закон сложения скоростей. Этот закон утверждает, что скорости одного и того же тела по отношению к разным системам отсчета связаны соотношением (1.3) vт1 vт 2 v21 . Здесь vт1 и vт 2 – скорости тела относительно первой и второй системы отсчета, v21 – скорость второй системы отсчета относительно первой. Закон сложения скоростей является векторным. Это означает, три вектора vт1 , vт 2 и v21 образуют треугольник векторного сложения, и соотношение между величинами скоростей vт1 , 8 vт 2 и v21 – такое же, как и между длинами сторон треугольника. Углы этого треугольника равны углам между направлениями скоростей vт1 , vт 2 и v21 . vт 2 vт1 v21 vт 2 v21 vт1 v21 vт1 vт 2 Примеры треугольников сложения скоростей приведены на рисунке, причем на среднем и правом рисунке приведены примеры «треугольников» скоростей в случаях, когда скорость тела в системе 2 и скорость системы 2 относительно системы 1 направлены одинаково (средний рисунок) и противоположно (правый рисунок). Из этих рисунков следует, что скалярное соотношение, аналогичное (1.3) для величин скоростей vт1 vт 2 v21 , справедливо только, если векторы vт 2 и v21 направлены одинаково (средний рисунок). Если же векторы vт 2 и v21 направлены противоположно, для значений скоростей справедливо соотношение vт1 vт 2 v21 (или наоборот vт1 v21 vт 2 , если v21 vт 2 ) – правый рисунок. Из этих рассуждений ясно, что поскольку в задаче 1.1.10 векторы скорости пассажира относительно поезда v2 и поезда относительно земли v1 направлены одинаково, скорость пассажира относительно земли равна v1 v2 (правильный ответ – 2). В задаче 1.2.1 ситуация обратная – вектор скорости первой машины относительно земли и второй машины относительно земли направлены противоположно. Поэтому v12 v1м, з v2 м, з 3v , направлен вектор v12 на север – правильный ответ 4. В задаче 1.2.2 эти идеи применяются к движению лодки по и против течения. Из закона сложения скоростей заключаем, что при движении лодки по течению ее скорость относительно земли равна v u , при движении против течения - v u ( v – скорость лодки в стоячей воде, u – скорость течения). Отсюда находим, что при движении лодки по течению, ее скорость относительно земли 15 км/ч, а 9 при движении против течения – 5 км/ч. Поэтому время движения между городами А и В по течению втрое больше времени движения лодки между этими городами против течения (ответ – 2). Все следующие задачи этой главы являютA ся более сложными, поскольку в них рассматS ривается движение не одного, а двух тел, а закон сложения скоростей используется в слуB O чаях, когда векторы скоростей не направлены 3S вдоль одной прямой. В задаче 1.2.3 встреча тел происходит в такой точке, что расстояния, пройденные первым и вторым телом, отличаются втрое (так как в три раза отличаются скорости тел). Поэтому при выходе из точки А тела встретятся в такой точке В, что длины дуг АВ отличаются в три раза. Следовательно, угол АОВ – прямой, и длина отрезка АВ равна 2R . (ответ 4). Если два тела, начав движение одновременно, движутся навстречу друг другу (задача 1.2.4), то время встречи тел t можно найти следующим образом. Так как тела двигались до встречи одинаковое время, они прошли расстояния v1t и v2t , сумма которых равна первоначальному расстоянию между телами tv1 tv2 t (v1 v2 ) l . Поэтому t l /(v1 v2 ) (ответ 2). Отметим, что данные в условии задачи ответы 3 и 4 имеют неправильную размерность – 1/с и потому могут быть отброшены сразу. Задача 1.2.5 решается с помощью таких соображений: время движения первого пешехода между городами t1 l / v1 , второго – t2 l / v2 , встречи пешеходов t l /(v1 v2 ) (см. предыдущую задачу). Отсюда l l l . t t1 t2 Сокращая в этой формуле величину l , получаем 1 1 1 1 1 1 3 1 ч ч , t t1 t2 4 2 4 или t 4 / 3 ч (правильный ответ – 1). 10 В задаче 1.2.6 начальное и конечное положения вагона и человека показаны на правой и левой частях рисунка. S S1 Отсюда заключаем, что разность перемещений вагона и человека равна длине вагона l . Поэтому время, через которое провожающий окажется около конца вагона, определяется из соотношения S S1 v1t v2t l . Из этой формулы находится время, а затем и расстояние, пройденное провожающим (ответ 1). Отметим, что ответы 3 и 4 могли быть отброшены сразу, поскольку не описывают случай одинаковых скоростей. Действительно, при одинаковых скоростях вагон никогда не обгонит провожающего, и расстояние, пройденное при «обгоне» провожающим, должно обратиться в бесконечность. Другими словами, ответ должен содержать нуль в знаменателе при v1 v2 . Задача 1.2.7 посвящена вычислению средней скорости движения на некотором пути, которая определяется как отношение этого пути к затраченному времени. Если расстояние между городами А и В равно S , то полное время движения между городами t складывается из времен, затраченных на первую и вторую половины пути t Отсюда находим vср S S . 2v1 2v2 2v1v2 48 км/ч (правильный ответ – 3). v1 v2 В задачах 1.2.8-1.2.9 закон сложения скоростей рассматривается в ситуациях, когда векторы vт1 , vт 2 и v21 направлены не вдоль одной прямой. В этом случае необходимо использовать закон сложения скоростей в векторной форме (1.3). Когда человек в поезде идет перпендикулярно направлению его движения (задача 1.2.8), 11 треугольник сложения скоростей (1.3) имеет вид, показанный на рисунке. vчз vчп vпз Здесь vпз – вектор скорости поезда относительно земли, vчп – вектор скорости человека относительно поезда, который по условию направлен перпендикулярно вектору vпз . Поэтому согласно закону сложения скоростей вектор скорости человека относительно земли vчз представляет собой гипотенузу прямоугольного треугольника, катетами которого являются векторы vпз и vчп (см. рисунок). Следовательно, величину скорости человека относительно земли можно найти по теореме Пифагора 2 vчз vпз2 vчп v12 v22 (ответ 3). Задачи 1.2.9. и 1.2.10 удобнее решать, переходя из той системы отсчета, в котоu рой задача поставлена (в системе отсчеvлз v та, связанной с землей) в некоторую друα гую систему, в которой рассматриваемое явление является более простым. При переправе через реку (задача 1.2.9) скорость лодки относительно земли зависит от траектории – на траекториях, направленных под острыми углами к течению, скорость лодки больше, чем на траекториях, на которых угол между скоростью лодки и скоростью течения – тупой. Поэтому время переправы по самой короткой траектории (перпендикулярной берегам) не является минимальным. Траекторию с минимальным временем переправы легко найти в системе отсчета, связанной с водой. В этой системе отсчета вода покоится, и, следовательно, минимальное время переправы достигается на такой траектории, на которой вектор скорости лодки относительно воды v перпендикулярен берегам реки. Поэтому вектор скорости лодки относительно земли на этой траектории наклонен под углом α arctg (v / u) к течению (см. рисунок). Под таким углом к берегу и расположена 12 траектория, на переправу по которой лодка затрачивает минимальное время (правильный ответ – 1). В задаче 1.2.10 рассматривается движение трех тел. В системе отсчета, связанной с землей ответ неочевиден. Быстрый катер дольше уплывет от лодки, но будет двигаться быстрее и при обратном движении, медленный – наоборот. Однако если перейти в систему отсчета, связанную с водой, решение очень несложно. В этой системе отсчета плот покоится, каждый катер при движении от плота и к плоту движется с одинаковой скоростью. Поэтому каждый катер вернется к плоту через то же самое время после разворота, в течение которого он двигался от плота. Следовательно, катера вернутся одновременно (ответ 3). 13





